【luogu P4097】【bzoj 3165】Segment（李超线段树）

Segment

题目链接：luogu P4097 / bzoj 3165

题目大意

要你动态支持两个操作。
加入一条线段，或者查询在某一个 x 坐标上哪一条线段对于的 y 值最大。

思路

这道题是李超线段树的模板题。

考虑线段树用标记永久化记录每个区间中会有的最优线段。
那查询就直接一路下去把每个位置都判断一下，就可以了，重点是如何插入一条线段。

我们考虑两条线段（新的线段和当前区间的最优线段）比较。
这里用的是通过区间中点两个线段的 \(y\) 值的大小关系和两个线段的斜率来比较。
那我们就可以先求出每条线段的斜率和截距。

首先我们规定红色线的斜率比粉色的大。

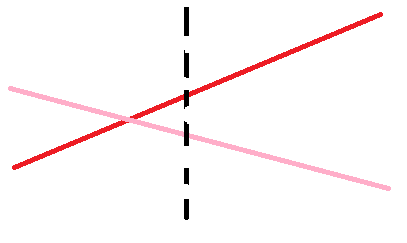
如果红色的大，那交点就会在左边，就是右边的一定是红色大，可以把这个区间的赋为红色的，然后左边再用粉色递归下去。

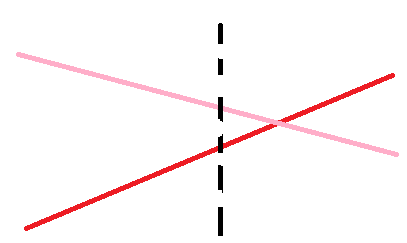
如果粉色的大，那交点就会在右边，那左边的就一定是粉色打，可以把这个区间的赋为粉色的，然后右边再用红色递归下去。

然后这么一直递归到只有一个点，就完成啦，复杂度是 \(logn\) 的。

当然这道题的线段是左右范围的，所以你还要通过线段树把它分割成 \(logn\) 份来解决，所以每次插入的复杂度是 \(log^2n\) 的。

然后这道题要特判一下一条竖线 \(k=0\) 的情况，就直接变成 \(y=\max(y_1,y_2)\) 就可以了。

代码

#include<cstdio>
#include<iostream>

using namespace std;

int n, lstans, op, x, y;
int x1, y1, q;
double k[100001], b[100001];

double f(int id, int x) {//计算第 id 条线段在 x 坐标对应的 y 值
	return k[id] * x + b[id];
}

struct XDtree {//李超线段树
	int s[40001 << 2];
	
	void up(int now, int l, int r, int L, int R, int x) {
		if (L <= l && r <= R) {//把区间分割成 logn 份
			if (l == r) {//递归到只有一个位置
				if (f(x, l) > f(s[now], l) || (f(x, l) == f(s[now], l) && x <= s[now])) {
					s[now] = x;
				}
				return ;
			}
			
			int mid = (l + r) >> 1;
			if (k[x] > k[s[now]]) {//每一份 logn 的复杂度标记永久花解决
				if (f(x, mid) > f(s[now], mid)) up(now << 1, l, mid, L, R, s[now]), s[now] = x;
					else up(now << 1 | 1, mid + 1, r, L, R, x);
			}
			else {
				if (f(x, mid) > f(s[now], mid)) up(now << 1 | 1, mid + 1, r, L, R, s[now]), s[now] = x;
					else up(now << 1, l, mid, L, R, x);
			}
			
			return ;
		}
		
		int mid = (l + r) >> 1;
		if (L <= mid) up(now << 1, l, mid, L, R, x);
		if (mid < R) up(now << 1 | 1, mid + 1, r, L, R, x);
	}
	
	int query(int now, int l, int r, int pl) {
		if (l == r) {
			return s[now];
		}
		
		int mid = (l + r) >> 1, y = 0;
		if (pl <= mid) y = query(now << 1, l, mid, pl);
			else y = query(now << 1 | 1, mid + 1, r, pl);
		if (f(s[now], pl) > f(y, pl) || ((f(s[now], pl) == f(y, pl)) && s[now] > y)) return s[now];
			else return y;
	}
}T;

int main() {
	scanf("%d", &q);
	for (int i = 1; i <= q; i++) {
		scanf("%d", &op);
		if (op == 0) {
			scanf("%d", &x);
			x = (x + lstans - 1) % 39989 + 1;
			lstans = T.query(1, 1, 39989, x);
			printf("%d\n", lstans);
		}
		else {
			scanf("%d %d %d %d", &x, &y, &x1, &y1);
			x = (x + lstans - 1) % 39989 + 1; y = (y + lstans - 1) % 1000000000 + 1;
			x1 = (x1 + lstans - 1) % 39989 + 1; y1 = (y1 + lstans - 1) % 1000000000 + 1;
			if (x > x1) swap(x, x1), swap(y, y1);
			++n;
			if (x1 != x) {//求出斜率
				k[n] = 1.0 * (y1 - y) / (x1 - x);
				b[n] = y - k[n] * x;
			}
			else {//特判一条竖线（k=0）的情况
				k[n] = 0;
				b[n] = max(y, y1);
			}
			T.up(1, 1, 39989, x, x1, n);
		}
	}
	
	return 0;
}