回文树（并查集）（倍增）（LCA）（ST 表）

回文树

题目大意

给你一棵树，然后你要给每个点给上一个字母。
有一些限制条件，要求某一段路径在填好之后是一个回文串。
问你总有有多少种方案满足限制条件。

思路

首先不难从回文串中看出它就是让一些位置规定要字母相同。
那关系之间就只有相同和任意。
那你就需要找到有多少互补相干的，那这么多个 $26$ 乘在一起就是答案了。

那接着不难想到用并查集，但你发现直接暴力维护就只能有 $20$ 分。
那你考虑怎么优化，这也是这题最神仙的地方。
看到树上操作，自然想到倍增，然后再加上并查集。
那就会想到把并查集和倍增搞到一起！！！
具体就是把每个倍增的区间都维护一个并查集，然后跑完所有限制条件再把它们全部下降到长度为 $1$。

那接着你考虑看树上路径要怎么相互配对：

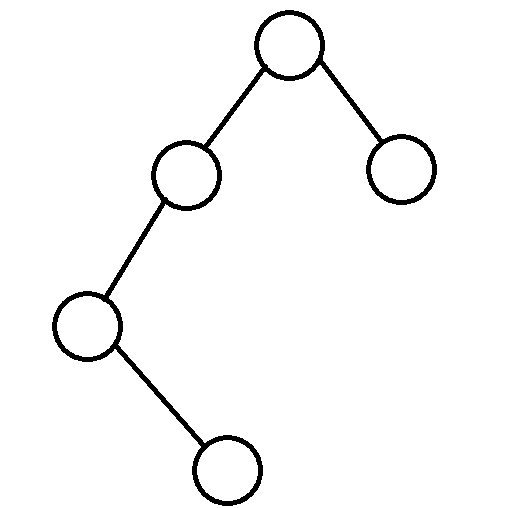
假设你要搞这条路径，我们把浅的到根以及他配对的找出来：

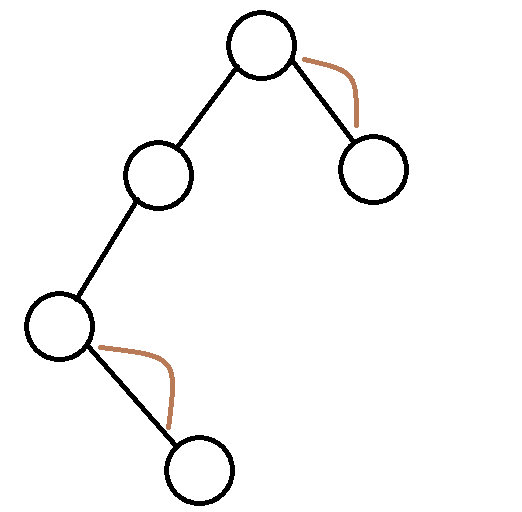
那接着另外一段也要匹配：

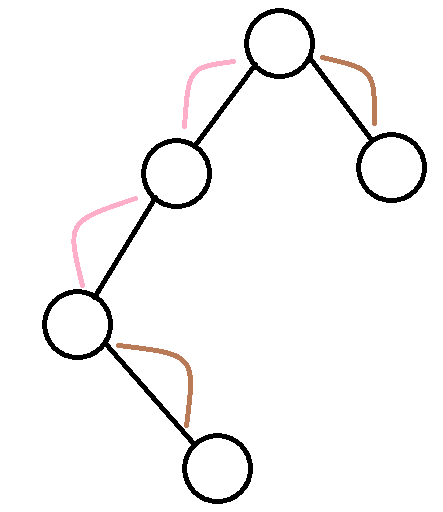
那你分别看这两段，棕色那段两段都是向上的，只要互相匹配就行了。
那你就搞一个倍增，把它分成 $logn$ 段，然后两两相互配对。
接着麻烦的是粉色的那一段，你会发现一个是向上，一个是向下的。

那就不难想到对于倍增的每个区间要搞两个并查集，一个是维护正的，一个是维护反的。
然后你看两个加起来长度固定，而且你想你把一个并查集反复放入另一个并查集跟放一次没有影响，不难想到一个东西可以快速求——ST表！！！

然后我们接着讲讲要怎么合并。

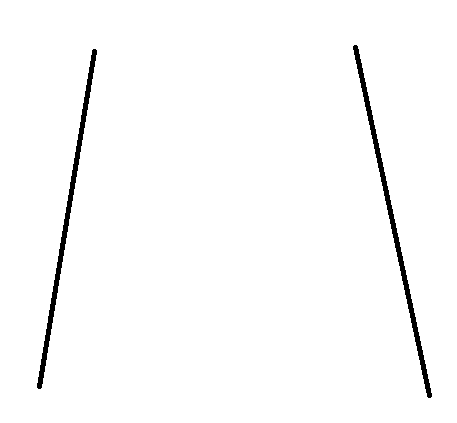
这是两段你要合并的路径：
因为是倍增的，你把它分成两段：

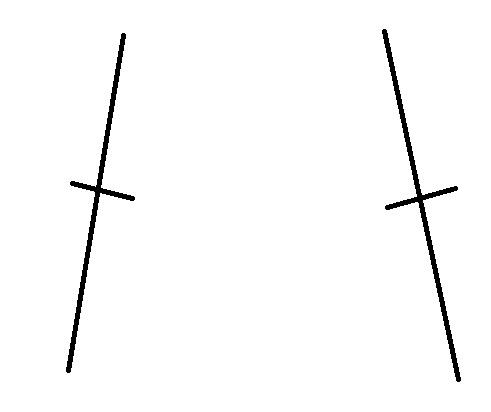
那如果两个都是正的，那就是这么配对：

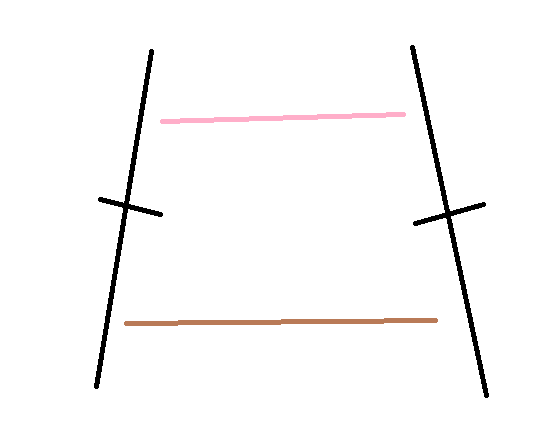
如果一正一反，就是这样：

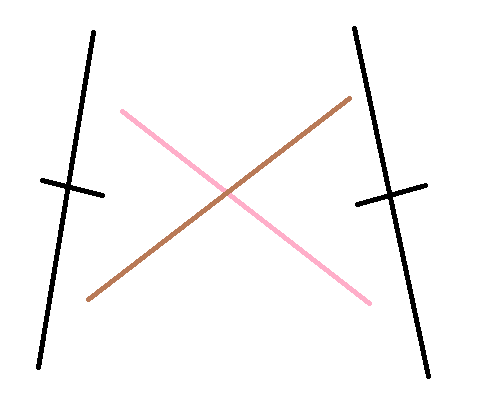
也许有人会想，你这不是要继续递归吗？
没错是可以，但这样会超时，我们可以就把它放在这里先，然后等所有限制都跑了之后，就把它给下传，下传也是像这样子的规则下传。

然后不难看出到最后如果正的和反的的父亲如果有一个是自己，那就说明它就代表了一个独立的。

然后就能统计出来了。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
#define mo 1000000007

using namespace std;

struct node {
	int to, nxt;
}e[200001];
int n, x, y, m, le[100001], KK;
int deg[100001], fa[100001][21];
int tot, fath[2][100001][21];
int sz[5000001], d[5000001][3];
int log2[100001], father[5000001];

void add(int x, int y) {
	e[++KK] = (node){y, le[x]}; le[x] = KK;
	e[++KK] = (node){x, le[y]}; le[y] = KK;
}

//倍增的预备 dfs
void dfs(int now, int father) {
	deg[now] = deg[father] + 1;
	fa[now][0] = father;
	
	for (int i = le[now]; i; i = e[i].nxt)
		if (e[i].to != father) {
			dfs(e[i].to, now);
		}
}

//求 LCA
int LCA(int x, int y) {
	if (deg[y] > deg[x]) swap(x, y);
	for (int i = 20; i >= 0; i--)
		if (deg[fa[x][i]] >= deg[y])
			x = fa[x][i];
	if (x == y) return x;
	for (int i = 20; i >= 0; i--)
		if (fa[x][i] != fa[y][i])
			x = fa[x][i], y = fa[y][i];
	return fa[x][0];
}

int jump(int now, int high) {
	for (int i = 20; i >= 0; i--)
		if (high >= (1 << i)) {
			high -= (1 << i);
			now = fa[now][i];
		}
	return now;
}

//并查集
int find(int now) {
	if (father[now] == now) return now;
	return father[now] = find(father[now]);
}

//合并并查集
void up(int ox, int x, int oy, int y, int k) {
	int X = find(fath[ox][x][k]), Y = find(fath[oy][y][k]);
	if (X == Y) return ;
	if (sz[X] > sz[Y]) swap(X, Y);
	father[X] = Y;
	sz[Y] += sz[X];
}

void merge(int ox, int x, int oy, int y, int num) {
	if (ox == oy) {//两个都是正的
		for (int i = 20; i >= 0; i--)
			if (num >= (1 << i)) {
				num -= (1 << i);
				up(ox, x, oy, y, i);
				x = fa[x][i];
				y = fa[y][i];
			}
		up(ox, x, oy, y, 0);
		return ;
	}
	
	//一正一反
	if (ox == 1) {
		swap(ox, oy);
		swap(x, y);
	}
	int dis = deg[x] - deg[y];
	for (int i = 20; i >= 0; i--)
		if (dis >= (1 << i)) {
			dis -= (1 << i);
			int fry = fa[jump(x, dis)][0];
			up(ox, x, oy, fry, i);
			break;//这里找到就 break，所以是 ST 表
			//这个 dis 是两段的加起来要的长度，所以只要刚好小于它就可以了
		}
	up(ox, x, oy, y, 0);
}

//快速幂
ll ksm(ll x, int y) {
	ll re = 1;
	while (y) {
		if (y & 1) re = (re * x) % mo;
		x = (x * x) % mo;
		y >>= 1;
	}
	return re;
}

int main() {
//	freopen("paltree.in", "r", stdin);
//	freopen("paltree.out", "w", stdout);
	
	scanf("%d", &n);
	for (int i = 1; i < n; i++) {
		scanf("%d %d", &x, &y);
		add(x, y);
	}
	
	log2[0] = -1;
	for (int i = 1; i <= n; i++)
		log2[i] = log2[i >> 1] + 1;
	
	dfs(1, 0);
	for (int i = 1; i <= 20; i++)
		for (int j = 1; j <= n; j++)
			fa[j][i] = fa[fa[j][i - 1]][i - 1];
	
	for (int i = 0; i <= 1; i++)
		for (int j = 1; j <= n; j++)
			for (int k = 0; k <= 20; k++) {
				fath[i][j][k] = ++tot;
				sz[tot] = 1;
				father[tot] = tot;
				d[tot][0] = i; d[tot][1] = j; d[tot][2] = k;
			}//初始化
	
	scanf("%d", &m);
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		int lca = LCA(x, y);
		if (deg[y] > deg[x]) swap(x, y);
		int nowrun = deg[y] - deg[lca];
		merge(0, x, 0, y, nowrun);//两个正的
		x = jump(x, nowrun);
		y = jump(y, nowrun);
		merge(0, x, 1, y, deg[x] - deg[y]);//一正一反
	}
	
	for (int i = 20; i >= 1; i--) {//把它下降会全部长度为 1 的
		for (int j = 1; j <= n; j++) {
			for (int k = 0; k <= 1; k++) {
				int x = fath[k][j][i];
				int X = find(x);
				if (x == X) continue;
				int x1 = k, x2 = j, x3 = i;
				int X1 = d[X][0], X2 = d[X][1], X3 = d[X][2];
				if (x1 == X1) {
					up(x1, x2, X1, X2, x3 - 1);
					up(x1, fa[x2][x3 - 1], X1, fa[X2][x3 - 1], x3 - 1);
				}
				else {
					if (x1 == 1) {
						swap(x1, X1);
						swap(x2, X2);
						swap(x3, X3);
					}
					up(x1, x2, X1, fa[X2][x3 - 1], x3 - 1);
					up(x1, fa[x2][x3 - 1], X1, X2, x3 - 1);
				}
				//注意这里也要分一正一反，两个正的
			}
		}
	}
	
	for (int i = 1; i <= n; i++)//最后一层
		up(0, i, 1, i, 0);
	
	int num = 0;//统计答案
	for (int i = 1; i <= n; i++)
		for (int j = 0; j <= 1; j++) {//正的或反的有一个可以就行
			if (find(fath[j][i][0]) == fath[j][i][0])
				num++;
		}
	
	printf("%lld", ksm(26, num));
	//记得你算出来的是互不相干的共多少个，所以答案是这么多个 26 乘在一起
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}

__EOF__

本文作者：あおいSakura
本文链接：https://www.cnblogs.com/Sakura-TJH/p/jzoj_4498.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！