kruskal重构树and笛卡尔树

为什么放在了一起

因为我个人旗帜鲜明的认为这是一个东西

前者可以旗帜鲜明的解决图上(包括树上)限定最值的联通问题

建立方式：跑kruskal时每连接两个点时建立一个新点 把原来两个点连到新点上 新点权值为边权

如图：(随便扒了一张)

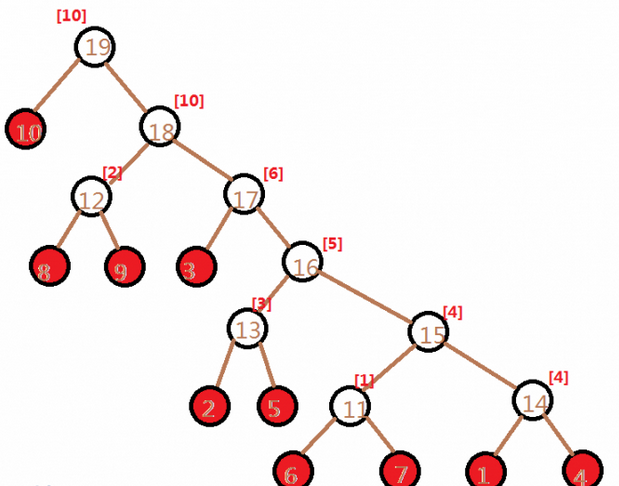
我们经过仔细的思考和严密的推理充分发扬人类的智慧再结合微不足道的oi-wiki和题解发现:

(以下默认最小生成树)

0、 一个点越往跟点权越大(原1-n点不考虑点权)(废话)

1、两点之间路径最大值即两点点权的lca(这很kruskal)

2、把1反过来 当起点为x 限定最大边权时 点权小于等于限定值的最靠近根的祖先内所有点你都可以到达

我们经过仔细的思考和严密的推理充分发扬人类的智慧再结合微不足道的oi-wiki和题解再次发现:

低配版kruskal只告诉你保留那几条边 没有保留树的形态 没有保留中途的改变

而保留了树的形态的重构版基于它的贪心性质堪比进行了可持久化了一样 可以在限定值不同时灵活处理

然后遇到题就可以乱搞了

考虑知道起点和限定值时如何求能直达的子树的根

因为离谱的值域范围我们考虑倍增

根据二进制拆分思想2的次幂从大到小祖先点权满足限定值就跳

加上对每一颗子树的预处理就可以乱搞通过kruskal为数不多的几道题

洛谷P4197Peaks P7834Peaks加强版

后者就是前者强制在线……

但是因为我们的重构kruskal简直跟自带可持久化一样所以我们肯定是在线的

我们经过仔细的思考和严密的推理充分发扬人类的智慧再结合微不足道的题解再再次发现:

还是得打可持久化线段树

倍增求出能到达的点所在子树的根

问题就变成了字数内第k大

肯定转成序列问题 如果不强制在线可以线段树合并搞

在线的话通过dfs序转成区间问题 用sandom树区间第k大解决

注意加强版图可能不连通

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#define Sakura int
#define Re register int
#define _ putchar(' ')
#define el putchar('\n')

using namespace std;

const int maxn=2e5+10;

inline int read(){
    int x=0,f=0;char c=getchar();
    while(!isdigit(c)) f|=c=='-',c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?-x:x;
}

inline void ot(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) ot(x/10);putchar(x%10|48);
}

struct Edge{
    int x,y,z;
};

inline bool operator<(const Edge &A,const Edge &B){
    return A.z>B.z;
}

struct Segtree{
    int Rt[maxn],lc[maxn*18],rc[maxn*18],sum[maxn*18],tot;
    int insert(int pre,int l,int r,int pos){
        int p=++tot;
        sum[p]=sum[pre]+1;
        if(l^r){
            int mid=l+r>>1;
            if(pos<=mid){
                lc[p]=insert(lc[pre],l,mid,pos);
                rc[p]=rc[pre];
            } 
            else{
                lc[p]=lc[pre];
                rc[p]=insert(rc[pre],mid+1,r,pos);
            }
        }
        return p;
    }
    int query(int pre,int p,int l,int r,int k){
        if(sum[p]-sum[pre]<k) return 0;
        if(l==r) return l;
        int res=sum[rc[p]]-sum[rc[pre]];
        int mid=l+r>>1;
        return k<=res?query(rc[pre],rc[p],mid+1,r,k):query(lc[pre],lc[p],l,mid,k-res);
    }
}tree;

vector<int> G[maxn];
priority_queue<Edge> q; 
int n,m,t;
int ans;
int a[maxn],b[maxn],cnt;
int val[maxn],tot;
int fa[maxn][18];
int c[maxn],tim,le[maxn],ri[maxn];
bool vis[maxn];

struct Dsu{
    int fa[maxn];
    void init(){
        for(Re i=1;i<=n*2;++i) fa[i]=i;
    }
    int find(int x){
        return fa[x]==x?x:fa[x]=find(fa[x]);
    }
    inline void merge(int x,int y){
        int r1=find(x),r2=find(y);
        fa[r2]=r1;
    }
}dsu;

void init(){
    n=read(),m=read(),t=read();
    for(Re i=1;i<=n;++i) a[i]=b[i]=read();
    while(m--){
        int x=read(),y=read(),z=read();
        q.push(Edge{x,y,z});
    }
    sort(b+1,b+n+1);
    cnt=unique(b+1,b+n+1)-b-1;
    for(Re i=1;i<=n;++i) a[i]=lower_bound(b+1,b+cnt+1,a[i])-b;
    // for(Re i=1;i<=n;++i) ot(a[i]),_;el;
}

void kruskal(){
    tot=n;
    dsu.init();
    while(tot<n*2-1&&!q.empty()){
        auto e=q.top();
        q.pop();
        int x=e.x,y=e.y,z=e.z;
        int r1=dsu.find(x),r2=dsu.find(y);
        if(r1==r2) continue;
        fa[r1][0]=fa[r2][0]=++tot;
        G[tot].push_back(r1);
        G[tot].push_back(r2);
        // ot(tot),_,ot(r1),_,ot(z),el;
        // ot(tot),_,ot(r2),_,ot(z),el;
        dsu.merge(tot,r1),dsu.merge(tot,r2);
        vis[r1]=vis[r2]=true;
        val[tot]=z;
    }
    for(Re j=1;j<18;++j)
        for(Re i=1;i<=tot;++i)
            fa[i][j]=fa[fa[i][j-1]][j-1];
}

void dfs(int u){
    le[u]=tim+1;
    if(u<=n) c[++tim]=a[u];
    for(auto v:G[u]) dfs(v);
    ri[u]=tim;
}

void build(){
    for(Re i=1;i<=tot;++i)
        if(!vis[i])
            dfs(i);
    // for(Re i=1;i<=tot;++i) ot(i),_,ot(le[i]),_,ot(ri[i]),el;
    for(Re i=1;i<=n;++i) tree.Rt[i]=tree.insert(tree.Rt[i-1],1,n,c[i]);
}

inline void solve(){
    int u=read(),limit=read(),k=read();
    for(Re i=17;i>=0;--i)
        if(fa[u][i]&&val[fa[u][i]]<=limit)
            u=fa[u][i];
    ans=b[tree.query(tree.Rt[le[u]-1],tree.Rt[ri[u]],1,n,k)];
    ans?ot(ans):ot(-1);el;
}

Sakura main(){
    init();
    kruskal();
    build();
    while(t--) solve();
}

洛谷P4768

我经过仔细的思考和严密的推理充分发扬人类的智慧再结合微不足道的题解之后

不想写了 自己看题解吧

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define Sakura int
#define Re register ll
#define _ putchar(' ')
#define el putchar('\n')
#define ll long long
#define fi first
#define se second
#define mp make_pair

using namespace std;

const ll maxn=4e5+10;
const ll inf=1e18;

inline ll read(){
    ll x=0,f=0;char c=getchar();
    while(!isdigit(c)) f|=c=='-',c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?-x:x;
}

inline void ot(ll x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) ot(x/10);putchar(x%10|48);
}

struct Edge{
    ll x,y,z;
};

inline bool operator<(const Edge &A,const Edge &B){
    return A.z<B.z;
}

ll T;

priority_queue<pair<ll,ll> > q1;
ll n,m,K,S;
ll ans;
ll tot,head[maxn],nextt[maxn<<1],ver[maxn<<1],w[maxn<<1];
ll dis[maxn];
bool vis[maxn];

priority_queue<Edge> q2;
vector<ll> G[maxn];
ll Fa[maxn],fa[maxn][20];
ll val[maxn];

inline void clear(){
    memset(vis,0,sizeof(vis));
    for(Re i=1;i<=n;++i) head[i]=0;
    for(Re i=1;i<=tot;++i) G[i].clear();
    tot=1;
    ans=0;
    while(!q2.empty()) q2.pop();
}

inline void add(ll x,ll y,ll z){
    ver[++tot]=y;
    w[tot]=z;
    nextt[tot]=head[x];
    head[x]=tot;
}

void dij(){
    memset(dis,60,sizeof(dis));
    dis[1]=0;
    q1.push(mp(0,1));
    while(!q1.empty()){
        ll u=q1.top().se;
        q1.pop();
        if(vis[u]) continue;
        vis[u]=true;
        for(Re i=head[u];i;i=nextt[i]){
            ll v=ver[i],z=w[i];
            if(dis[v]>dis[u]+z){
                dis[v]=dis[u]+z;
                q1.push(mp(-dis[v],v));
            }
        }
    }
    // for(Re i=1;i<=n;++i) ot(dis[i]),_;el;
}

ll find(ll x){
    if(x==Fa[x]) return x;
    return Fa[x]=find(Fa[x]);
}

void dfs(ll u){
    if(u<=n) return;
    dis[u]=inf;
    for(auto v:G[u]){
        dfs(v);
        dis[u]=min(dis[u],dis[v]);
    }
}

void kruskal(){
    tot=n;
    for(Re i=1;i<=n*2;++i) Fa[i]=i;
    while(tot<n*2-1){
        auto e=q2.top();
        q2.pop();
        ll x=e.x,y=e.y,z=e.z;
        ll r1=find(x),r2=find(y);
        if(r1==r2) continue;
        Fa[r1]=Fa[r2]=++tot;
        val[tot]=z;
        fa[r1][0]=fa[r2][0]=tot;
        G[tot].push_back(r1);
        G[tot].push_back(r2);
        // ot(tot),_,ot(r1),el;
        // ot(tot),_,ot(r2),el;
    }   
    dfs(tot);
    for(Re j=1;j<20;++j)
        for(Re i=1;i<=tot;++i)
            fa[i][j]=fa[fa[i][j-1]][j-1];
    // for(Re i=1;i<=tot;++i) ot(i),_,ot(dis[i]),_,ot(val[i]),el;
    // for(Re i=1;i<=tot;++i){
    //     for(Re j=0;j<=2;++j) ot(fa[i][j]),_;
    //     el;
    // }
}

void solve(ll v,ll p){
    for(Re i=19;i>=0;--i)
        if(val[fa[v][i]]>p)
            v=fa[v][i];
    // _,ot(v),el;
    ans=dis[v];
    ot(ans),el;
}

Sakura main(){
    T=read();
    while(T--){
        clear();
        n=read(),m=read();
        while(m--){
            ll x=read(),y=read(),z1=read(),z2=read();
            add(x,y,z1);
            add(y,x,z1);
            q2.push(Edge{x,y,z2});
        }
        dij();
        kruskal();
        m=read(),K=read(),S=read();
        while(m--){
            ll v=(read()+K*ans-1)%n+1;
            ll p=(read()+K*ans)%(S+1);
            solve(v,p);
        }
    }
}

然后我们学习笛卡尔树

发现它和上面那个就是一丘之貉

我单方面宣称重构kruskal就是笛卡尔树上树

至于为什么

我要咕

回来了