6.7-6.8CFdiv3瞎打（关于IOI打成ACM这件事）EFG

 

 

 

 垃圾翻译：

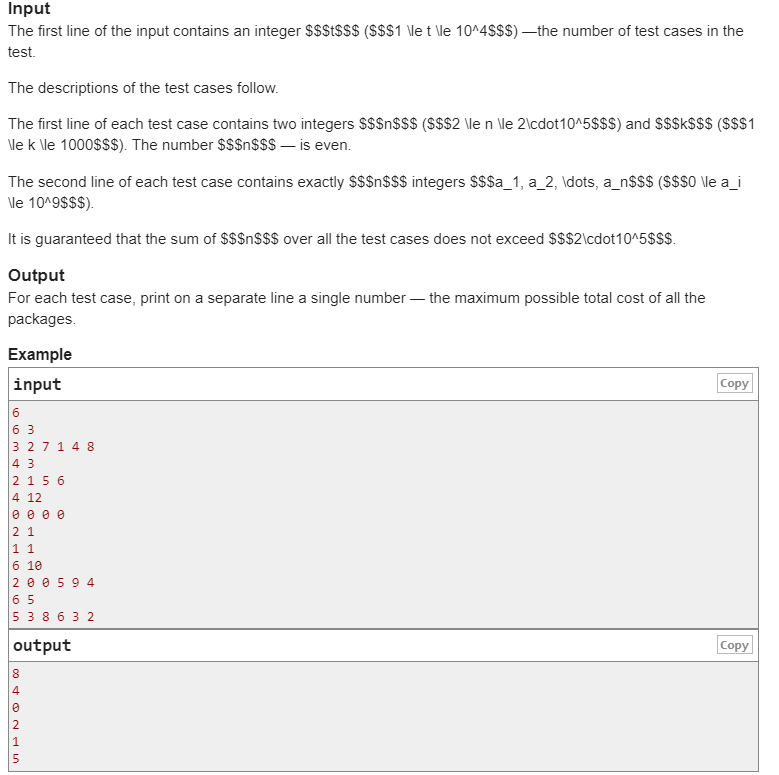
 题不难 不过有点思维含量

 首先 先对所有重量取模得到余数

我们要使更多余数配对大于零

贪心yyds

对余数开个桶 两个指针两端开扫

对于当前最大值 让它尽量跟小的配对

而如果左指针的最小值不能跟右指针的最大值配对 就不存在一个更大的数跟它配对

如果我们拆掉原来的配对 结果也不会变得更优

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#define Sa Sakura 
#define Re register int
#define _ putchar(' ')
#define el putchar('\n')
#define maxn 200010

using namespace std;

inline int read(){
    int f=0,x=0;char c=getchar();
    while(c<'0'||c>'9') f|=c=='-',c=getchar();
    while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return f?-x:x;
}

inline void ot(long long x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) ot(x/10);putchar(x%10|48);
}

int t,a[maxn],n,b[maxn],k,q[maxn],top;

main(){
    t=read();
    while(t--){
        top=0;
        int ans=0;
        n=read(),k=read();
        for(Re i=1;i<=n;i++){
            a[i]=read();
            ans+=a[i]/k; 
            a[i]%=k;
            if(a[i]) q[++top]=a[i];
        }
    //    _,ot(ans),el;
        sort(q+1,q+top+1);
//        for(Re i=1;i<=top;i++)
//            ot(q[i]),_;el;
        int l=1,r=top;
        while(l<r){
            while(l<r&&q[l]+q[r]<k)
                l++;
            if(l==r)
                break;
            ans++;
            l++,r--;
        }
        ot(ans),el;
    }
}

 

 

 

 

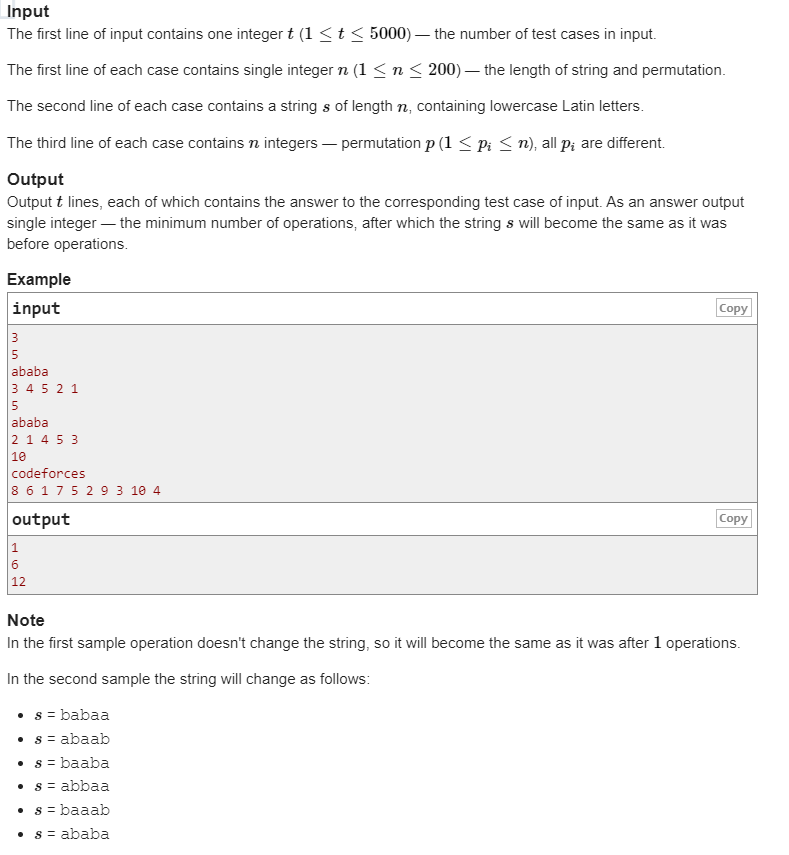
Polycarp 找到了字符串 s 和排列 p。结果证明它们的长度相同并且等于 n。

n 个元素的排列 — 是一个长度为 n 的数组，其中从 1 到 n 的每个整数恰好出现一次。例如，[1,2,3] 和 [4,3,5,1,2] 是排列，但是 [1,2,4], [4,3,2,1,2] 和 [0,1 ,2] 不是。

在一次操作中，他可以将 s 与 p 相乘，因此他将 s 替换为字符串 new，其中对于从 1 到 n 的任何 i，newi=spi 是真的。例如，当 s=wmbe 和 p=[3,1,4,2] 时，操作后字符串会变成 s=s3s1s4s2=bwem。

Polycarp 想知道在经过多少次操作后，该字符串将首次等于其初始值。由于可能需要很长时间，他在这件事上请求您的帮助。

可以证明所需的操作次数总是存在的。它可能非常大，因此请使用 64 位整数类型。

输入 输入的第一行包含一个整数 t (1≤t≤5000) — 输入中的测试用例数。

每个案例的第一行包含单个整数 n (1≤n≤200) — 字符串的长度和排列。

每个 case 的第二行包含一个长度为 n 的字符串 s，其中包含小写拉丁字母。

每个case的第三行包含n个整数——排列p（1≤pi≤n），所有的pi都是不同的。

 

个人认为比G题有思维含量一点（毕竟G题就是数据结构难打……）

首先建边后各自成环

在环上每个字母不同时 答案为环长的最大公约数

然而有相同的

发现每个环上字符串回到初始状态所需次数不变

（废话 但是我没看出来）

所以我们所需的其实是最小循环节的lcm

kmp

#include<bits/stdc++.h>
#define Sa Sakura 
#define Re register int
#define _ putchar(' ')
#define el putchar('\n')
#define int long long
#define maxn 50010

using namespace std;

inline int read(){
    int f=0,x=0;char c=getchar();
    while(c<'0'||c>'9') f|=c=='-',c=getchar();
    while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return f?-x:x;
}

inline void ot(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) ot(x/10);putchar(x%10|48);
}

int t,n,ans,nextt[maxn],a[maxn],top;
bool ju[maxn];
char s[maxn],q[maxn];

void dfs(int x){
    ju[x]=true;
    q[++top]=s[x];
    if(!ju[a[x]])
        dfs(a[x]);
}

inline void KMP(){
    nextt[1]=0;
//    for(Re i=1;i<=top;i++)
//        cout<<q[i];cout<<endl;
    for(Re i=2,j=0;i<=top;i++){
        while(j>0&&q[i]!=q[j+1]) j=nextt[j];
        if(q[i]==q[j+1]) 
            j++;
        nextt[i]=j;
    }
}

inline int gcd(int x,int y){
    if(!y) return x;
    return gcd(y,x%y);
}

inline void lcm(){
    int len=top-nextt[top];
//    _,_,ot(len),el;
    if(top%len)
        len=top;
//    _,ot(len),el;
    ans=ans*len/gcd(ans,len);
}

main(){
    t=read();
    while(t--){
        n=read();
        ans=1;
        for(Re i=1;i<=n;i++)
            scanf(" %c",&s[i]);
        for(Re i=1;i<=n;i++)
            a[i]=read(),ju[i]=false;
        for(Re i=1;i<=n;i++)
            if(!ju[i]){
                top=0;
                dfs(i);
                KMP();
                lcm();
            }
        ot(ans),el;
    }
}

 

 

 

 

 

 

 

 

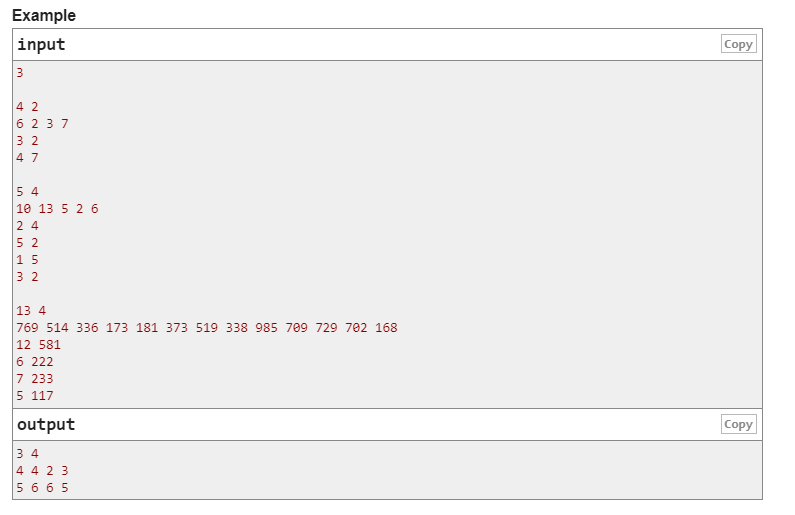
 首先 降低的是最大速度而非当前速度（然后我们就省了一个query函数……）

区间维护 我永远喜欢线段树

原数组不好维护 维护不上升数组（即实际速度）

每个区间维护火车左速度（根据不上升一定为区间最大速度） 右速度（一定为区间最小速度） 火车数

有点染色的感觉

修改很恶心 但是我们用瞎打战术

找出这个车降低后的最大速度 只要这辆车即之后的车运行速度大于它就lazy

所以只要我们打上一堆乱七八糟的限制条件

只要这个区间有可能被修改 就跑它一遍

你只管瞎打 剩下的交给递归……

#include<bits/stdc++.h>
#define Sa Sakura 
#define Re register int
#define _ putchar(' ')
#define el putchar('\n')
#define int long long
#define maxn 100010

using namespace std;

inline int read(){
    int f=0,x=0;char c=getchar();
    while(c<'0'||c>'9') f|=c=='-',c=getchar();
    while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return f?-x:x;
}

inline void ot(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) ot(x/10);putchar(x%10|48);
}

int t,n,a[maxn],sum[maxn*4],lv[maxn*4],rv[maxn*4],m,b[maxn];
bool lazy[maxn*4];

inline void pushdown(int p){
    if(!lazy[p])
        return;
//    ot(666),_,ot(p),el; 
    lazy[p<<1]=lazy[p<<1|1]=true;
    lazy[p]=false;
    lv[p<<1]=rv[p<<1]=lv[p<<1|1]=rv[p<<1|1]=lv[p];
    sum[p<<1]=sum[p<<1|1]=1;
}

inline void pushup(int p){
    sum[p]=sum[p<<1]+sum[p<<1|1];
    if(rv[p<<1]==lv[p<<1|1])
        sum[p]--;
    lv[p]=lv[p<<1],rv[p]=rv[p<<1|1];
}

void build(int p,int l,int r){
    lazy[p]=false;
    if(l==r){
        sum[p]=1;
        lv[p]=rv[p]=a[l];
        return;
    }
    int mid=l+r>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
    pushup(p);
//    _,ot(l),_,ot(r),_,ot(sum[p]),_,ot(lv[p]),_,ot(rv[p]),el;
}

void change(int p,int l,int r,int x,int d){
    if(lv[p]<=d)
        return;
    if(r<x)
        return;
    if(x<=l&&rv[p]>=d){
    //    _,ot(l),_,ot(r),_,ot(lv[p]),_,ot(rv[p]),el;
        lazy[p]=true;
        lv[p]=rv[p]=d;
        sum[p]=1;
        return;
    }
    int mid=l+r>>1;
    pushdown(p);
    if(x<=r&&lv[p<<1|1]>d)
        change(p<<1|1,mid+1,r,x,d);
    if(x<=mid&&lv[p<<1]>d)
        change(p<<1,l,mid,x,d);
    pushup(p);
}

main(){
//    freopen(".out","w",stdout);
    t=read();
    while(t--){
        n=read(),m=read();
        for(Re i=1;i<=n;i++){
            b[i]=a[i]=read();
            if(i!=1)
                a[i]=min(a[i-1],a[i]);
        }
//        for(Re i=1;i<=n;i++)
//            ot(a[i]),_;el;
        build(1,1,n);
    //    _,_,_,ot(sum[1]),el; 
        while(m--){
            int x=read(),d=read();
        //    _,ot(b[x]-d),el;
            change(1,1,n,x,b[x]-d);
            ot(sum[1]),_;
            b[x]-=d;
        }el;
    }
}