高考期间集训混打(为了防止hzoi后来的学弟们发现这有一个博客都懒得打的学长 今天开始写博客)
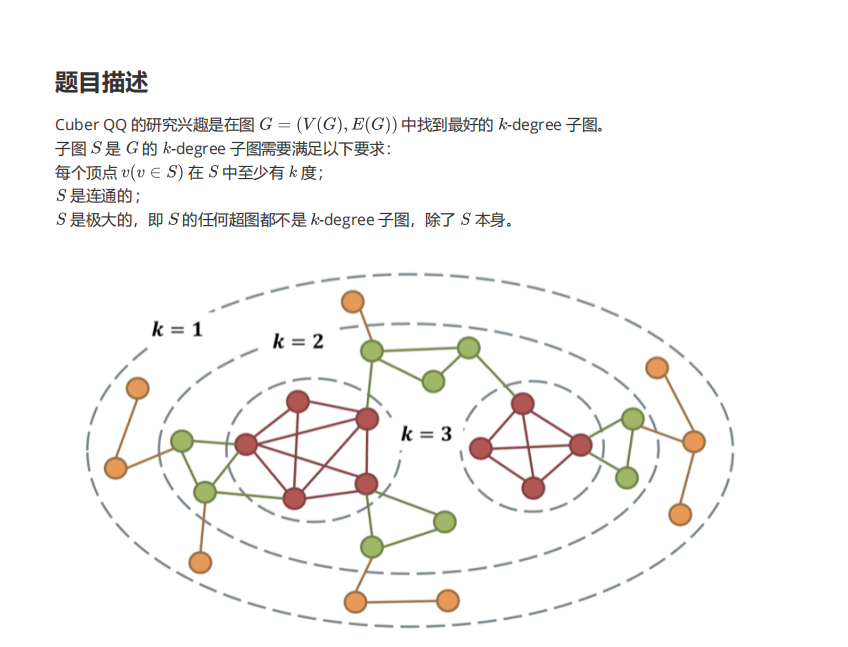

首先子图中点的dg只算它在这个子图中的dg(看图)
分裂难搞 最难搞的是分裂出来的子图可能不连通
eafoo n方过百万被lyin hack了
所以我们逆分裂——合并——并查集
先拓扑拆图 每个点归到它所在最高级图里
每个点初始边界边数就是dg n为1 m为0
如果两个非同一集合的点连边
n相加 m相加再加1 边界边相加-2
因为这两条边在两个集合各算一次边界边 合并变成一条集合内的边
如果已经是同一集合
边界边-2,m++;
剩下好搞了

#include<bits/stdc++.h> #define Sa Sakura #define Re register int #define _ putchar(' ') #define el putchar('\n') #define maxn 1000010 using namespace std; inline int read(){ int f=0,x=0;char c=getchar(); while(c<'0'||c>'9') f|=c=='-',c=getchar(); while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar(); return f?-x:x; } inline void ot(int x){ if(x<0) putchar('-'),x=-x; if(x>9) ot(x/10);putchar(x%10|48); } vector<int> G[maxn],S[maxn]; int n,m,N,M,B,l,r,fa[maxn],ns[maxn],bs[maxn],ms[maxn],dg[maxn],cnt,ansk,q[maxn],be[maxn]; long long ans=-99999999999999999; int find(int x){ if(fa[x]==x) return x; return fa[x]=find(fa[x]); } inline void merge(int x,int y){ int r1=find(x),r2=find(y); // _,ot(r1),_,ot(r2),el; if(r1==r2){ bs[r1]-=2; ms[r1]++; }else { fa[r2]=r1; ns[r1]+=ns[r2]; bs[r1]+=bs[r2]-2; ms[r1]+=ms[r2]+1; } } main(){ freopen("kdgraph.in","r",stdin); freopen("kdgraph.out","w",stdout); n=read(),m=read(); M=read(),N=read(),B=read(); for(Re i=1;i<=m;i++){ int v=read(),u=read(); G[u].push_back(v); G[v].push_back(u); dg[u]++; dg[v]++; } l=1,r=0; for(Re i=1;i<=n;i++){ fa[i]=i; ns[i]=1; bs[i]=dg[i]; } int cnt=0; int maxx=0; for(Re i=0;i<n;i++){ for(Re j=1;j<=n;j++) if(dg[j]==i) if(!i) cnt++; else q[++r]=j; if(!i) continue; while(l<=r){ int u=q[l]; // ot(i),_,ot(u),el; l++; S[i].push_back(u); be[u]=i; cnt++; for(Re j=0;j<G[u].size();j++){ int v=G[u][j]; dg[v]--; if(dg[v]==i) q[++r]=v; } } l=1,r=0; if(cnt==n){ maxx=i; break; } } // for(Re i=1;i<=maxx;i++){ // for(Re j=0;j<S[i].size();j++) // ot(S[i][j]),_; // el; // } // ot(cnt),_,ot(maxx),el; for(Re i=maxx;i>0;i--){ for(Re j=0;j<S[i].size();j++){ int u=S[i][j]; for(Re k=0;k<G[u].size();k++){ int v=G[u][k]; if(i<be[v]||(i==be[v]&&u<v)) merge(u,v); } } for(Re j=0;j<S[i].size();j++){ int u=S[i][j]; int r1=find(u); long long res=(long long)M*ms[r1]-(long long)N*ns[r1]+(long long)B*bs[r1]; // ot(i),_,ot(r1),_,ot(res),el; // ot(ms[r1]),_,ot(ns[r1]),_,ot(bs[r1]),el; if(res>ans){ ans=res; ansk=i; } } } cout<<ansk<<" "<<ans; }
交通
离谱二分图思想
进阶指南里的二要素和一要素思想嘛
每个点两个同类型的边选一个
每个边视为一个点
这两个点建边
然后跑二分图————个屁 我们要求的是方案数
显然映射出来是一对不连通的环
因为原图中一条边连接两个点 所以映射之后它也有两个与它相连的点
发现同一个点上相同类型的边映射成点后在一个简单环上
所以一定是偶环
点数为2n的偶环 选n个不相邻的点
2种情况
所以乘法原理总结果 $2^{环数}$
并查集维护

#include<bits/stdc++.h> #define Sa Sakura #define Re register int #define _ putchar(' ') #define el putchar('\n') #define maxn 100010 #define mod 998244353 using namespace std; inline int read(){ int f=0,x=0;char c=getchar(); while(c<'0'||c>'9') f|=c=='-',c=getchar(); while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar(); return f?-x:x; } inline void ot(int x){ if(x<0) putchar('-'),x=-x; if(x>9) ot(x/10);putchar(x%10|48); } int n,fa[maxn*2],in[maxn][3],out[maxn][3],cnt; int find(int x){ if(fa[x]==x) return x; return fa[x]=find(fa[x]); } int qpow(int x,int d){ int an=1; while(d){ if(d&1) an=an*x%mod; x=x*x%mod; d>>=1; } return an; } main(){ freopen("a.in","r",stdin); freopen("a.out","w",stdout); n=read(); for(Re i=1;i<=n*2;i++) fa[i]=i; for(Re i=1;i<=n*2;i++){ int u=read(),v=read(); out[u][++out[u][0]]=i; in[v][++in[v][0]]=i; } for(Re i=1;i<=n;i++){ int e1=in[i][1],e2=in[i][2]; int r1=find(e1),r2=find(e2); fa[r2]=r1; e1=out[i][1],e2=out[i][2]; r1=find(e1),r2=find(e2); fa[r2]=r1; } for(Re i=1;i<=n*2;i++) if(find(i)==i) cnt++; ot(qpow(2,cnt)); }
冒泡排序
很神一道题
对于判无解 直接跑冒泡排序
表面上复杂度$n^{2}$
实际上一个位置不可能动两次
复杂度就玄学起来 反正不是n ……
就可以卡过
假如一个数要从a移动到b(a<b) 那么显然交换有一个次序
就有了pre和nex数组
宇墨大佬太强了
想出了以i为递推的式子
如果i是i-1前驱 前i个点里i的局部拓扑序要比i-1小
反之亦然
如果没关系那就瞎搞
具体在代码里

//好好的dp我为什么要打数论 #include<bits/stdc++.h> #define Sa Sakura #define Re register int #define _ putchar(' ') #define el putchar('\n') #define maxn 5010 #define int long long #define mod 1000000007 using namespace std; inline int read(){ int f=0,x=0;char c=getchar(); while(c<'0'||c>'9') f|=c=='-',c=getchar(); while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar(); return f?-x:x; } inline void ot(int x){ if(x<0) putchar('-'),x=-x; if(x>9) ot(x/10);putchar(x%10|48); } int n,a[maxn],b[maxn],ans,f[maxn][maxn]; bool ju[maxn],pre[maxn],nex[maxn]; bool judge(){ int cnt=0; for(Re i=1;i<=n;i++) b[i]=a[i]; for(Re i=n;i>1;i--){ for(Re j=1;j<i;j++){ if(b[j]>b[j+1]){ // ot(b[j]),_,ot(b[j+1]),el; if(ju[j]) return false; ju[j]=true; swap(b[j],b[j+1]); cnt++; if(cnt>n) return false; } } // _;for(Re i=1;i<=n;i++) ot(a[i]),_;el; } // _,ot(cnt),el; if(cnt!=n-1) return false; return true; } signed main(){ freopen("mp.in","r",stdin); freopen("mp.out","w",stdout); n=read(); for(Re i=1;i<=n;i++) a[i]=read()+1; if(judge()==false){ ot(0); return 0; } for(Re i=1;i<=n;i++) if(a[i]>i) for(Re j=i+1;j<a[i];j++) pre[j]=true; else for(Re j=a[i]+1;j<i;j++) nex[j]=true; f[1][1]=1; // for(Re i=1;i<=n;i++) // ot(pre[i]),_; // el; // for(Re i=1;i<=n;i++) // ot(nex[i]),_; // el; //pre i-1是否为i前驱 //nex i是否为i-1前驱 //f[i][j]中j表示局部拓扑序 for(Re i=2;i<n;i++)//到n-1因为只有n-1个交换位点 if(pre[i])//i-1为i前驱 j=2:i至少为第二个动的 for(Re j=2;j<=i;j++) f[i][j]=f[i-1][j-1]+f[i][j-1],f[i][j]%=mod; //这波复杂度直接降了个n yumo大佬tql //前一个点是自己的前驱 先于自己动 else if(nex[i])//i为i-1前驱 for(Re j=i-1;j>=1;j--) f[i][j]=f[i][j+1]+f[i-1][j],f[i][j]%=mod;//接着卡复杂度 //在i-1个点中第i-1个点的拓扑序为j 那么把i插入到i-1之前 //i-1拓扑序变为j+1 所以 f[i][j]可以由f[i-1][j]递推 //因为f[i-1][j]中的j是指在i-1的点里的拓扑序 else{ for(Re j=1;j<i;j++) f[i][1]+=f[i-1][j],f[i][1]%=mod; for(Re j=2;j<=i;j++) f[i][j]=f[i][1];//又卡了一波复杂度 //二者平行 拓扑序没有直接关系 可以由任何状态递推 } // for(Re i=1;i<n;i++){ // ot(i),_; // for(Re j=1;j<n;j++) // ot(f[i][j]),_; // el; // } for(Re i=1;i<n;i++) ans+=f[n-1][i],ans%=mod; ot(ans); //神仙dp方式 我只能想到状压和数论 //弄掉复杂度的方式也很巧妙 }
这题我吹爆!!!收获很大
首先sum不递增 一般来说跑不了斜率
然而我们思考
一般斜率 有 i j 两个量 由&n^{2}$优化到n
但是这个题有三个相关量 i j k
想不到斜率优化原因是如果贸然排序可能会造成无序
那么那么那么
看j!!!
假如 $\forall$k,k<j,$\forall$i,i>j
那么任意选出一个k 一个 i 与固定的 j 搭配 一定合法
所以那就
固定j!
然后k跑单调队列 i排序
$n^{2}$
很神
主要是有枪毙自己的 更神了
无入度一定活 那他指的人一定死
有点dp感觉 这个人活不活着我们不太关心 只关心他开不开枪
最多好说 入度为0的点加上没有外来的点指向的环数就是最少剩下的
当然自杀的睿智另说……
多活的话
我们发现只要能不杀就不杀就最优
证明 :凭感觉……
所以对于非环 拓扑
剩下的环 如果环上有必死点 剩下当链处理
裸环至少要死(size+1)/2个

//怎么能分类讨论这么多种情况?? //杀人的艺术 //没事枪毙自己有病四八 没ser干帮我调代码来 //你想枪毙你自己?正好 我也想 #include<bits/stdc++.h> #define Sa Sakura #define Re register int #define _ putchar(' ') #define el putchar('\n') #define maxn 1000010 using namespace std; inline int read(){ int f=0,x=0;char c=getchar(); while(c<'0'||c>'9') f|=c=='-',c=getchar(); while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar(); return f?-x:x; } inline void ot(int x){ if(x<0) putchar('-'),x=-x; if(x>9) ot(x/10);putchar(x%10|48); } stack<int> s; int n,a[maxn],q[maxn],l=1,r=0,ydhz,dg[maxn]; bool bxhz[maxn],knhz[maxn]; main(){ freopen("maf.in","r",stdin); freopen("maf.out","w",stdout); //我能学到什么? 我的思路偏向了哪? //你能不能活着 我不关心 //你开不开枪 我才在乎 //我关心你:开枪的可能性 //活着一定开枪 死了可能开枪 //没有一个人是无辜的 n=read(); for(Re i=1;i<=n;i++){ a[i]=read(); dg[a[i]]++; } for(Re i=1;i<=n;i++) if(!dg[i]) q[++r]=i,ydhz++;//维护可能活着的 while(l<=r){ int x=q[l++]; if(bxhz[a[x]]) continue; bxhz[a[x]]=true;//能活着就能开枪 int ldbx=a[a[x]]; dg[ldbx]--; knhz[ldbx]=true; if(!dg[ldbx]) q[++r]=ldbx; } for(Re i=1;i<=n;i++) if(dg[i]&&bxhz[i]==false){//环 int size=0; bool ju=false; for(Re j=i;bxhz[j]==false;j=a[j]){ size++; if(knhz[j]) ju=true; bxhz[j]=true; } if(ju==false&&size>1) ydhz++; r+=size/2; } ot(n-r),_,ot(n-ydhz); }



