「剑指offer」 JZ55-二叉树的深度

「剑指offer」 JZ55-二叉树的深度

描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度，根节点的深度视为 1 。

数据范围：节点的数量满足 0-100，节点上的值满足0-100
进阶：空间复杂度O(1),时间复杂度O(n)

假如输入的用例为{1,2,3,4,5,##6,##,7}，那么如下图:

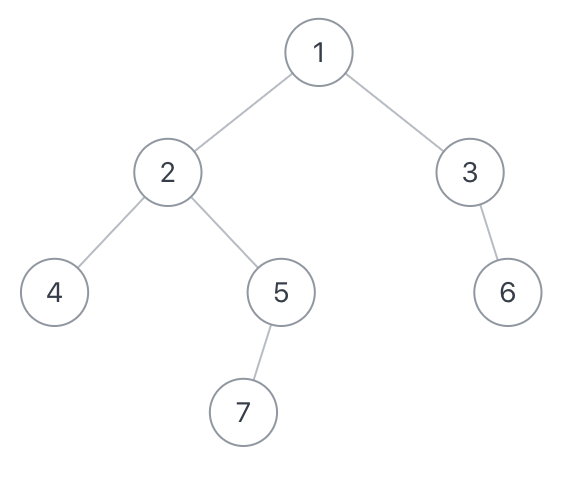
示例1

输入：{1,2,3,4,5,#,6,#,#,7}
返回值：4

示例2

输入：{}
返回值：0

我的题解

我是采用了树的广度遍历的思想，通过树的广度优先遍历的过程来逐层逐层获取树的层高，因为树的广度优先遍历是逐层来遍历树的节点，在实现时可以通过一个队列或者两个栈等多种方式来实现。

import java.util.Stack;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
        //特殊情况
             //树为空
        if(root==null){
            return 0;
        }
        //普通情况解决，求树的深度其实可以使用树的广度优先便利来做
        //通过将树中的节点分层来防止在容器中，就可以求出来树总共有多少层
        Stack<TreeNode> tempA = new Stack();
        Stack<TreeNode> tempB = new Stack();
        tempA.push(root);
        int level = 0;
        while(!tempA.isEmpty()){
            level+=1;
            while(!tempA.isEmpty()){
                TreeNode tempNode = tempA.pop();
                if(tempNode.left!=null){
                    tempB.push(tempNode.left);
                }
                if(tempNode.right!=null){
                    tempB.push(tempNode.right);
                }
            }
            Stack<TreeNode> tempC = tempA;
            tempA = tempB;
            tempB = tempC;
        }
        return level;
        
    }
}

时间复杂度 O(/N/)：/N/ 为树的节点数量，层序遍历计算树的深度也要遍历所有节点
空间复杂度O(/N/)：使用了栈来帮助实现层序遍历，N为队列长度

学习到的新解法

方法一：分治递归法

思想：
该方法是利用树天生的可以用于递归的特性，采用左右子树分治求解。

	分治法简介:
		求一个规模为n的问题，先求左边规模大约为n/2的问题，再求右边规模大约为n/2的问题，然后合并左边，右边的解，从而求得最终解。具体可参考归并排序。 步骤：
	1	求 pro(left, rigth) -> int
	2	先求pro(left, (left+right)/2) -> lval
	3	再求pro((left+right)/2 + 1, right) -> rval
	4	merge(lval, rval) -> result

在一般的解法中，基本就可以不用管最终函数是具体如何实现的，但是当你写好代码之后，自然而然函数就实现了。

代码：

public class Solution {
	public int TreeDepth(TreeNode root) {
		if(root==null){return 0;}
		int left = TreeDepth(root.left);
		int right = TreeDepth(root.right);
		returnn Math.max(left,right)+1;
	}
}

我的评价：
这种解法的话复杂度会比较高，但是会比较好想，我会一般不去这样想用递归的方式来做，一般我会选择递归作为动态规划的前摇。
时间复杂度 O(/N/)：/N/ 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度O(/N/)：N为递归时需要开辟的额外栈空间，用于递归方法堆栈