可学习的D-AMP算法：基于压缩图像恢复准则的神经网络（Learned D-AMP: Principled Neural Network Based Compressive Image Recovery）

可学习的D-AMP算法：

基于压缩图像恢复准则的神经网络

​ Christopher A. Metzler； Ali Mousavi； Richard G. Baraniuk

摘要

​ 压缩图像恢复是一个极具挑战的问题，它要求快而精确的算法。近年来，神经网络技术被应用于该问题并得到了有效的结果，通过使用大量的并行CPU处理数据和大量的数据，运行速度可以比现有的技术快几个数量级。然而这些方法大部分都是没有规则的黑盒子，不仅训练难度大，而且通常只是针对矩阵。

​ 近期有证明，迭代的稀疏信号恢复算法可以被展开形成可解释的（不同于黑匣子的只知道输出结果而不知道处理过程）的深度网络。我们从该证明中获得灵感，构建了一个新的神经网络来模仿基于去噪的近似消息传递算法（D-AMP）的框架。我们将这个网络称为LDAMP。

​ LDAMP网络易于训练可以应用于许多不同的测量矩阵，状态演化方程可以精确的预测性能。更重要的是它再精度和运行时间方面的性能均超过了现在比较先进的技术BM3D-AMP算法和NLR-CS算法。再高分辨率下，当与具有快速实现的感知矩阵一起使用时，LDAMP运行速度比BM3D-AMP快50倍，比NLR-CS快数百倍。

1. 介绍

​ 在过去的几十年里，计算成像系统再许多不同的图像领域得到了大量的发展，从合成孔径雷达到功能MRI和CT扫描仪。这些系统大多数是通过\(y=Ax+\epsilon\)，来获取兴趣信号线性测量值\(y\)。其中，\(x \in R^n\)（信号），\(y\in R^m\)（测量值），\(\epsilon \in R^m\)（噪声）。

​ 计算成像系统的目的是再给定测量值\(y\)和测量矩阵\(A\)的条件下恢复信号\(x\)，当\(m<n\)时，该问题时欠定的（未知多于已知），并且必须利用x的先验知识才能恢复信号。这个问题被广泛的认为压缩采样。

​ 使用先验知识来从压缩测量中恢复图像\(x\)的方法有很多。下面我将简要的介绍其中几种方法。从简单的手动设计模型（传统方法）到完全的数据驱动方法（可学习的方法）做图，如Figure 1所示。

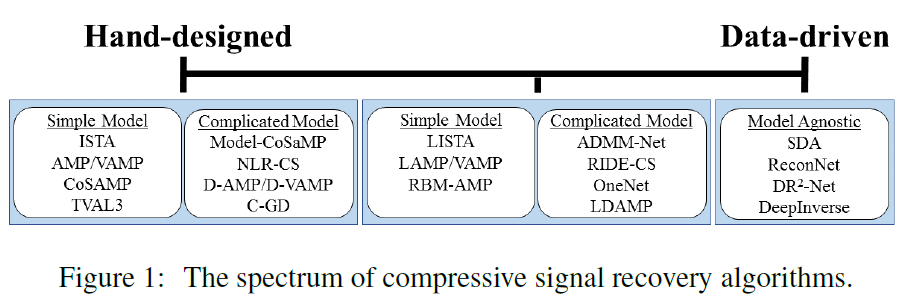
1.1 手工设计恢复算法

​ 绝大多数cs恢复算法由于使用了某种经验知识（即：先验，\(x\)的结构）可以被认为是手工设计的。最常见的信号先验是\(x\)在某些基上是稀疏的。使用稀疏先验的算法包括CoSAMP，ISTA，近似消息传递（AMP）和VAMP等等。研究人员还开发了更精确地描述自然图像结构的先验和算法，例如，最小总变量（TVAL3）,基于小波系数的马尔科夫数模型（CoSaMP）和局部自相似性（NLR-CS）。先成的去噪和压缩算法也被应用于重构上以加强先验，例如，基于去噪的AMP（D-AMP）,D-VAMP和C-GD。当应用于自然图像时，使用高级先验的算法性能优于使用简单先验（如小波稀疏）的算法。

​ 手工设计的方法的优势在于它们基于可解释性的先验，并且通常具有易于理解的行为。此外，当它们被设置为凸优化问题时，通常具有理论收敛保障。不幸的是在那些对信号使用精确先验的算法中，对于许多实时应用来说，即使是最快的算法也太慢了。更重要的是，这些算法没有用到潜在的训练数据。正如我们接下来将看到的，这留下了很大的改进空间。

1.2 数据驱动恢复算法

​ 在另一端是数据驱动的（通常是基于深度学习的）方法，它们不使用任何手工设计的模型。相反，研究人员提供了大量训练数据的神经网络（NNs），这些网络学习如何在数据中最好的利用结构。

​ 第一篇应用这种方法的论文是[13]，作者使用堆叠去噪自动解码器（SDA）从欠采样测量中恢复信号。这一分支的其他论文使用纯卷积层（深度逆[15]），或卷积层和全连接层（DR2-NET[16],ReconNet[14]）的组合来构建能够解决CS恢复问题的深度学习框架。如[13]所示，这些方法在精度方面可以与最先进的方法（传统的方式）相媲美，同时运行速度快了数千倍。不幸的是，这些方法的发展由于几乎没有理论保障它们的性能而受到阻碍，到目前为止，它们必须针对特定的测量举证和噪音水平来进行训练。

1.3 混合手工设计和数据驱动的恢复方法

​ 第三类恢复算法是将数据驱动与手工设计的算法结合。这些方法首先利用经验知识设置恢复算法，然后使用训练数据来学习这个算法的先验。这种算法具有从训练数据中学习更多真实信号先验的能力而获益，同时保持可解释性和保障性（手工设计方法的优势）。此类算法可以分成两个子类。第一个子类使用执行某些算法功能的黑匣子神经网络进行调整。第二个子类使用的展开迭代算法转换为一个深度神经网络，展开之后可以利用训练数据对网络进行调整。我们的LDAMP算法同时使用了这两种方法。

​ 黑匣子神经网络：用一个有规则的方法使用神经网络来解决CS问题的最简单方法就是把它当作一个执行某些函数的黑匣子（如计算后验概率）。这种方法的例子包括RBM-AMP以及一般化[18-20],使用受限的玻尔兹曼机制来学习非独立分布先验；EIDE-CS，使用RIDE[22]生成模型计算给定图像估计的概率；OneNet[23]使用神经网络作为近似映射/去噪器。

​ 展开的算法：第二种有规则的使用NN来解决压缩感知问题的方法就是简单的采用一个易于理解的恢复算法并展开它。这种算法有LISTA和LAMP神经网络来作为很好的说明。作者分别简单的展开了ISTA和AMP迭代算法，然后将算法的参数作为学习的权重。展开后训练数据可以通过网络进行反馈，随机梯度下降可以用来更新和优化参数。最近，展开的方法被应用于ADMM算法来解决CS-MRI问题。除了CS问题，该原理成功应用于语音增强，非负矩阵分解，音乐转录等。在这些应用中，展开和训练显著的提高了信号重建的质量和速度。

2. Learned D-AMP

2.1 D-IT 和 D-AMP

​ LDAMP是一种混合手工设计/数据驱动的基于D-AMP算法的压缩信号恢复框架。我们现在描述D-AMP以及更简单的基于去噪的迭代阈值算法（D-IT）。具体来讲，这些算法一般没有损失函数，而我们的关注点在于图像恢复。

​ 一个压缩图像恢复算法在给定低纬测量值\(y=Ax\)，通过利用x的先验信息，求图像\(x\)的不定适反问题。例如\(x\in C\)，其中\(C\)是所有自然图像的集合。一个很自然的优化公式如下：

\[argmin_x||y-Ax||_2^2 \ \ subject\ \ to\ \ x \in c \]

当没有测量噪声出现时，压缩图像算法应该返回集合c和拟合子平面\(\{x|y=Ax\}\)的交点，图像\(x_0\)（期望时唯一的），如Figure 2所示。

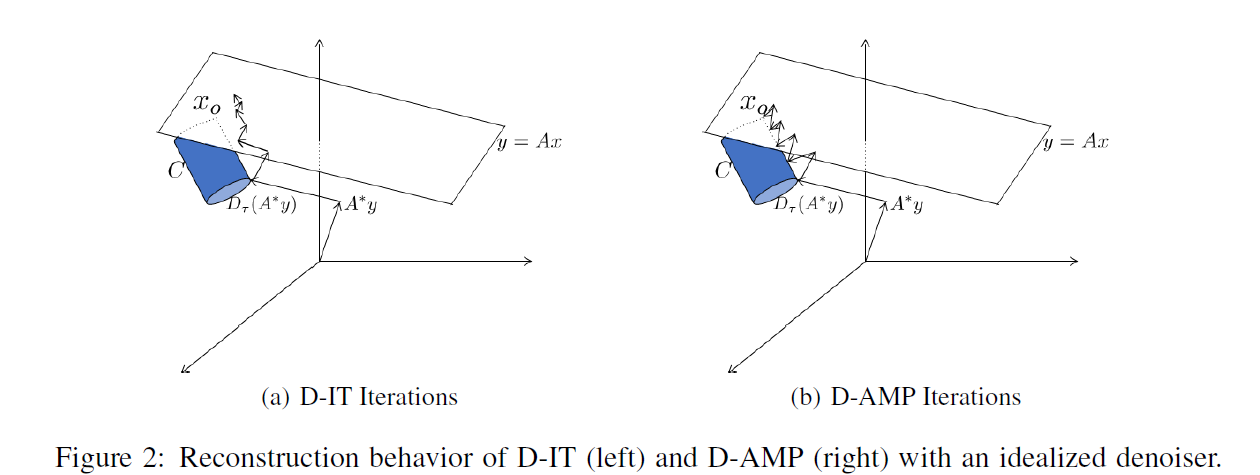
​ 应用D-IT和D-AMP的前提时高性能的图像去噪器\(D_\sigma\)（表明去噪器可以是使用噪声的标准差来参数化，去噪器可以被当作关于自然图像的负对数似然近似映射或对自然图像的数据生成函数进行梯度处理），例如BM3D，是自然图像集合\(C\)上的高质量近似映射。假定\(x_0+\sigma z\)是一个自然图像的噪声观测值，其中\(x_0 \in C\)并且\(z \sim N(0,I)\)。一个理想的去噪器\(D_\sigma\)可以简单的在集合\(C\)中找到最接近观测值\(x_0+\sigma z\)的点。

\[D_\sigma = argmin_x||x_0+\sigma z - x||^2_2 \ \ subject\ \ to \ \ x \in C \]

​ 结合（1）和（2）很自然的得出D-IT算法，如式（3）和Figure 2(a)所示。从\(x^0=0\)开始逐步拟合子空间\(\{x|y=Ax\}\)并应用去噪器\(D_\sigma\)将点移动到自然图像集合\(C\)中的\(x^1\)。梯度步进和去噪一直重复\(t=1,2,...\)直到收敛。

\[D-IT \ Algorithm:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{gather*} z^t = y -Ax^t \\ x^{t+1}=D{\hat{\sigma}^t}(x^t+A^Hz^t) \end{gather*}\tag{3} \]

​ 令\(v^t = x^t+A^Hz^t-x_0\)表示每次迭代\(x^t+A^Hz^t\)和真实信号\(x_0\)的差。\(v^t\)是有效噪声。每次迭代D-IT对\(x^t+A^Hz^t=x_0+v^t\)（即真实信号加有效噪声）去噪。大多数去噪器是针对\(v^t\)是加性高斯白噪声（AWGN）来设计的。不幸的是，随着D-IT迭代的增加，去噪器的中键结果会造成偏差，不久\(v^t\)就偏离AWGN。随后去噪迭代的作用会降低并且收敛很慢。

​ D-AMP与D-IT不同之处在于它使用Onsager校正项\(b^t\)修正了每次迭代时有效噪声的偏差\(t=1,2,...\)

\[D-AMP\ Algorithm: \ \ \ \ \begin{gather*} b^t = \frac{z^{t-1}div\hat{\sigma}^{t-1}(x^{t-1}+A^Hz^{t-1})}{m}\\ z^t = y-Ax^t+b^t\\ \hat{\sigma}^t = \frac{||z^t||_2}{\sqrt{m}}\\ x^{t+1} = D_{\hat{\sigma}^t}(x^t+A^Hz^t) \end{gather*}\tag{4} \]

​ Onsager修正项消除了中间解的偏差，使得有效符合典型图像去噪器所期望的AWGN模型。有关Onsager修正，它的起源以及它与Thouless-Anderson-Palmer方程的联系参见参考文献。注意$ \frac{||z^t||_2}{\sqrt{m}}$是一个使用精确的\(v^t\)标准差的估计。典型的，D-AMP算法对散度\(dicD(.)\)使用蒙特卡洛近似，在文献[37,10]中首次介绍。

2.2 去噪卷积神经网络

​ NNs在信号去噪方面有着悠久的历史，参见[38].然而直到最近，他们才开始明显优于BM3D等已建立的传统方法。在这一部分，我们将回顾最近开发的去噪卷积神经网络（DnCNN）图像去噪，比传统方法更准确速度更快。

​ DnCNN神经网络由16到20层组成结构如下。第一个卷积层使用64种不同的3X3Xc滤波器（其中c表示颜色通道的数量），然后再使用一个修正线性单元（ReLU）。接下来的14或18个卷积层分别使用64个不同的3X3X64的滤波器来重构信号。通过残差学习来学习参数。

2.3 将D-IT和D-AMP展开到网络中

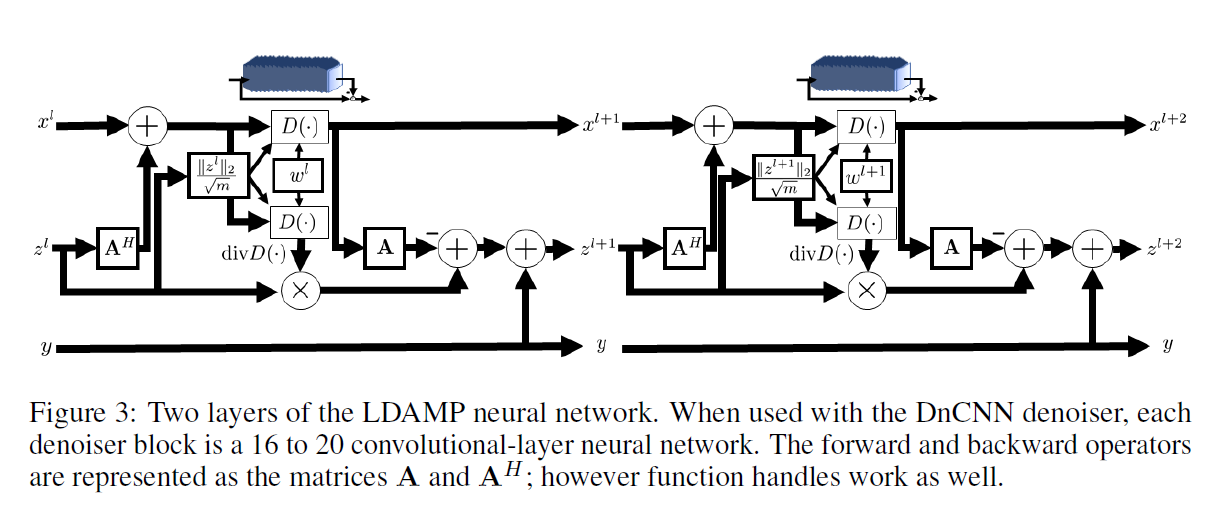
​ 这项工作的核心贡献是对D-IT和D-AMP应用了1.3种描述的展开的思想来构造LDIT和LDAMP神经网络。LDAMP网络如式（5）和Figure 3所示，包含10个AMP层，其中每个AMP层包含两个带有固定权重的去噪器。一个去噪器用于更新\(x^l\)，另一个用于使用蒙特卡洛近似来估计散度。LDIT网络几乎是相同的但是不需要计算Onsager矫正项每层只应用一个去噪器。展开D-IT和D-AMP的一个挑战是训练，我们需要使用一个易于传播梯度的去噪器，像BM3D这样的黑匣子去噪器将不能起作用，这限制了我们使用如DnCNN这样的去噪器。幸运的是，这样做却提高了性能。

\[LDAMP\ Neural\ Network:\ \ \ \ \begin{gather*} b^l = \frac{z^{l-1}div{D^l_{w^{l-1}(\hat{\sigma} ^{l-1})}}(x^{l-1}+A^Hz^{l-1})}{m}\\ z^l = y-Ax^l+b^l\\ \hat{\sigma}^l = \frac{||z^l||_2}{\sqrt{m}}\\ x^{l+1} = D_{w^l(\hat{\sigma}^l)}(x^l+A^Hz^l) \end{gather*}\tag{5} \]

​ 在（5）中我们使用了较为笨重的\(D_{w^l(\hat{\sigma}^l)}\)来表示网络的I层所使用的去噪器\(D^l\)，该去噪器依赖于它的权重/偏差\(w^l\),这些权重可能是噪声标准差估计\(\hat{\sigma}^l\)的函数。训练期间我们学习的参数仅有去噪器权重\(w^1,...w^l\)。这不同于LISTA和LAMP网络，作者将\(A\)和\(A^H\)矩阵从网络中解耦来学习。

3. 训练LDIT和LDAMP网络

​ 我们的实验中用三种不同的方法来训练LDIT和LAMP网络。这里我们将宏观的描述这些训练方法，细节将在第5部分进行描述。

• 端到端训练：我们同时训练所有的网络权重，这是训练神经网络的基本方法。
• 逐层训练：我们训练一个AMP层网络（包含一个16-20层的去噪器）来恢复信号，固定这些权重，增加一个AMP层，训练第二层，用两层网络的结果来恢复信号，固定这些权重并且重复直到我们需要的10层网络。
• 逐个去噪器训练：我们将去噪器从网络其他不服解耦，每个去噪器都基于不同噪声水平的AWGN问题训练。在推理过程中，网络利用其对噪声标准差的估计来选择使用哪一组噪声权重。注意，在选择要使用的噪声权重时，我们必须离散噪声水平的期望范围。例如，如果\(\hat{\sigma}=35\)w，我们需要噪声标准差的范围在20-40.

​ 随机梯度下降理论表明逐层和逐个去噪器训练相比较端到端训练会牺牲一定的性能。在4.2节中我们将会证明该条理论并不使用于LDAMP。对LDAMP而言，逐层和逐个去噪器训练是最小均方误差最优的。这些理论结果可以由Figure 4(a)和Figure 4(b)中的实验得出。这一部分的每个测试网络都是由10层的包含由16层DnCNN的去噪器的DAMP/DIT的展开层组成。

​ Figure 4(a)表明，根据理论LDAMP的逐层训练时最优的。此外，端到端的训练并不能增加网络的性能。与此相反，由表可知LDIT的逐层训练代表了典型神经网络行为，它是次优的。此外端到端训练明显提高性能。

​ 尽管理论表明，逐个去噪器训练时最优的，Fifure 4(a)表明LDAMP的逐个去噪器训练比逐层和端到端训练网络性能略差。这种性能上的差异很可能时由于噪声水平离散化并不是在我们的理论上建模而造成的。通过使用更精细的噪声水平离散化或者使用更深的去噪器网络可以更好的处理噪声水平范围，以降低这种差异。

​ 在Figure 4(b)中，我们报告了在某一采样率下训练在另一采样率下测试的两个网络的性能。LDIT和DAMP网络在采样率为0.2时的端到端训练和逐层训练的性能比在采样率0.05测试时的性能差。相反的，逐个去噪器训练网络，不针对特定采样率训练，可以很好的推广到不同的采样率。

4. LDAMP的理论分析

​ 本节有两个理论贡献。第一个，我们展示了状态演化（SE），一个用于预测AMP/D-AMP性能的框架，也适用于LDAMP。第二个，我们使用SE来证明LDAMP的逐层和逐个去噪器训练是MMSE最优的。

4.1 状态演化

​ 在LAMP和LDAMP的背景下，SE方程可以预测网络中的每一层的中间MSE。$\theta ^0 = \frac{||x_0||^2_2}{n} $开始，SE通过下列迭代生成一个数的序列：

\[\theta^{l+1}(x_0,\delta,\sigma_\epsilon^2)=\frac{1}{n}E_\epsilon||D^l_{w^l(\sigma)}(x_0+\sigma^l_\epsilon)-X_0||^2_2 \tag{6} \]

​ 其中\((\sigma^l)^2=\frac{1}{\delta}\theta^{l}(x_0,\delta,\sigma_\epsilon^2)+\sigma_\epsilon^2\)，标量\(\sigma_\epsilon\)是测量噪声\(\epsilon\)的标准偏差，期望服从分布\(\epsilon \sim N(0,1)\)。注意符号\(\theta^{l+1}(x_0,\delta,\sigma_\epsilon^2)\)是用来强调\(\theta^l\)可能依赖于信号\(x_0\)，不确定的\(\delta\)和测量噪声。令\(x^l\)表示LDAMP的L层的估计值。我们的实证结果如Figure 5所示，证明LDAMP的MSE可以由SE准确预测。下面开始正式描述我们的发现。

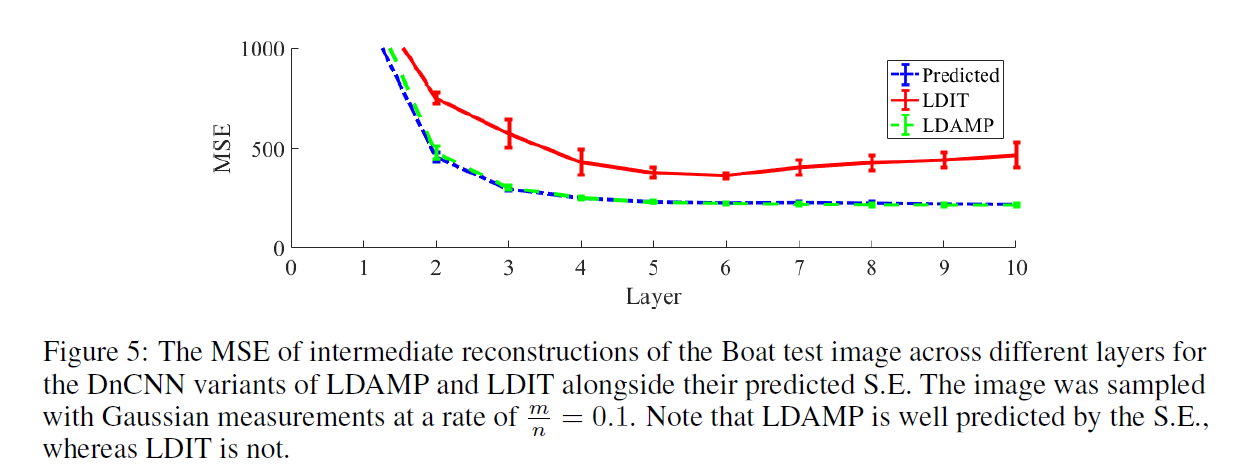
​ 发现1：如果LDAMP网络从\(x^0=0\)作为起始点那么对于值很大的\(m\)和\(n\)，SE预测了在每一层LDAMP的MSE，即\(\theta^{l}(x_0,\delta,\sigma_\epsilon^2)\approx \frac{1}{n}||x^l-x_0||\)，如果下列条件满足：（1）矩阵A的元素是独立同分布的高斯（或亚高斯）有均值为0或标准差1/m。(2)噪声\(w\)也是独立同分的高斯。（3）每一层的去噪器\(D^l\)是利普西茨连续的。

2.2 逐层和逐个去噪器训练是最优的

​ SE框架可以证明一下结论：LDAMP的逐层和逐个去噪器训练是MMSE最优的。这两个结果都依赖于下列引理。

​ 引理1：假设\(D^1,D^2,...D^L\)是单调的去噪器，在\(l=1,2,...L\)上有意义。\(inf_{w^l}E||D^l_{w^l(\sigma)}(x_0+\sigma\epsilon)-x_0||^2_2\)是关于\(\sigma\)的非增函数。如果\(D^1\)的权重\(w^1\)是用来最小化\(E_{x_0}[\theta^1]\)并固定，然后\(D^2\)的权重\(w^2\)是用来最小化\(E_{x_0}[\theta^2]\)并固定，....，之后\(D^L\)的权重\(w^L\)是用来最小化\(E_{x_0}[\theta^L]\)

​ 引理1可以用[10]中引理3的证明方法得到，但是要用\(E_{x_0}[\theta^L]\)来代替\(\theta_l\)。它可以引出一下两个推论。

​ 推论1：在引理1的条件下，LDMP的逐层训练时MMSE最优的。这个结论来自于引理1\(E_{x_0}[\theta^L]\)与\(E_{x_0}[\frac{1}{n}||x^l-x_2||^2_2]\)等价性。

​ 推论2：在引理1条件下，LDAMP的逐个去噪器训练是MMSE最优。这个结论来自于引理1的\(E_{x_0}[\theta^L]\)与\(E_{x_0}[\frac{1}{n}E_\epsilon||D^l_{w^l(\sigma)}(x_0+\sigma\epsilon)-x_0||^2_2]\)的等价性。

5.实验

​ 数据集：训练图像取自Berkeley 's BSD-500数据集。从这个数据集，我们使用了400张图像进行训练，50张用于验证，50张用于测试。由第三部分所示结果可知，训练图像被裁剪，缩放，翻转和旋转，形成一组204800重叠的40x40的补丁。验证图像被裁剪成1000个非重叠的40x40的补丁。我们使用了256个非重叠的40x40的补丁进行测试。对于本节所示结果，我们使用382464个50x50的补丁用于训练，652850个50x50的补丁用于验证，和7个标准测试图像，如Figure 6所示，并缩放到不同的分辨率进行测试。

​ 实现：我们实现LDAMP和LDIT，使用DnCNN去噪器，在TensorFlow和MatConvnet（Matlab工具箱）中，这两个版本的实现都可在该网站获得：https://github.com/ricedsp/D-AMP_Toolbox。

​ 训练参数：我们使用Adam优化器和训练率0.001来训练所有网络，当验证错误停止改进时，训练率降至0.0001然后是0.00001。根据网络大小和内存使用情况我们使用32到256个补丁的批次。对于逐层和逐去噪器训练，我们对每一个批次使用不同的随机生成矩阵。训练在Nvidia Pascal Titan X上通常每个去噪器的训练需要3到5小时。本节的结果是对逐去噪器训练网络（有10个展开的DAMP/DIT层组成，每层包含一个20层的DnCNN去噪器）的。

​ 竞争：我们将LDAMP的性能与三种最先进的图像恢复算法进行了比较；TVAL3，NLR-CS，和BM3D-AMP。我们还与LDIT进行了比较，以证明Onsager校正项的好处。我们的结果不包括其他的基于神经网络的方法的比较。许多基于神经网络的方法都是很单一化的，只使用于某些特定的矩阵。最近提出的OneNet和RIDE-CS方法可以得到更普遍的应用。不幸的是，我们无法对OneNet代码进行及时的训练和测试。虽然RIDE-CS代码是可使用的但是它的实现要求测量矩阵具有正交的行。当在非正交行的矩阵上测试时，该方法的性能比其他方法差的多。

​ 算法参数：所有算法使用它们的默认参数。然而，NLR-CS使用BM3D-AMP的8次迭代进行初始化，如[10]中所示。BM3D-AMP进行10次迭代。LDIT和LDAMP使用10层。LDIT有它的每层的噪声标准差估计参数\(\hat{\sigma}\)来设置\(2||z^l||2/\sqrt{m}\)就像[10]D-IT所作的那样。

​ 测试设置：我们用独立同分布的高斯测量和由一个随机采样的编码衍射图样得到的测量值来测试算法。编码衍射图样的前行操作由三个步骤组成；随机（均匀）改变相位，做2DFFT，随机（均匀）亚采样。除了Figure 7中的结果，我们用128x128的图像测试算法。我们用PSNR来报告恢复精度。然后报告运行时间（以秒为单位）。结果在补充中提供了图像分解的结果。

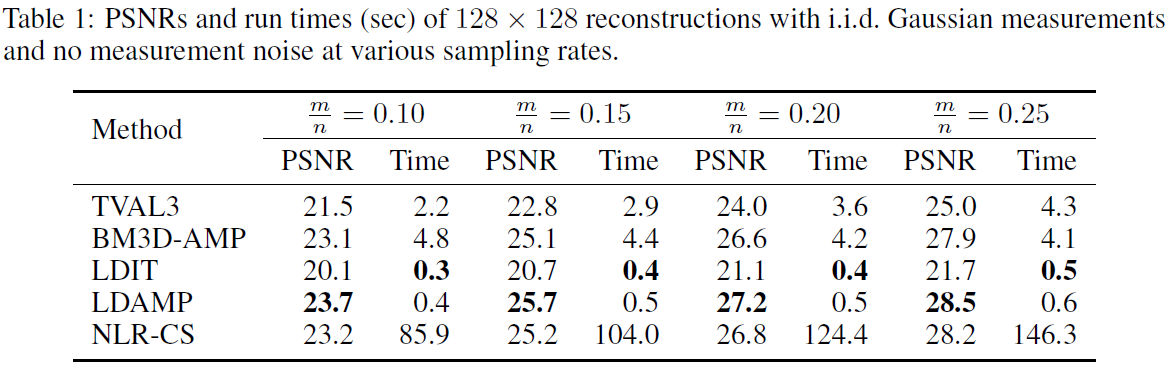
​ 高斯测量：在无噪声高斯测量的情况下，LDAMP网络在每个图像的每个采样率上产生最好的重构，除了指纹，与网络训练用的自然图像很不同。在无噪声高斯测量下，LDIT和LDAMP产生的重构信号速度明显快于竞争方法。注意，尽管必须要执行两次去噪操作，在采样率为0.25的LDAMP网络仅仅比LDIT网络慢大约25%左右。这意味着矩阵乘是计算的主要来源而不是去噪操作。表1中报告了平均恢复的PSNRs和运行时间。在高斯噪声下LDAMP平均水平优于其他方法；这些结果可以在补充中找到。

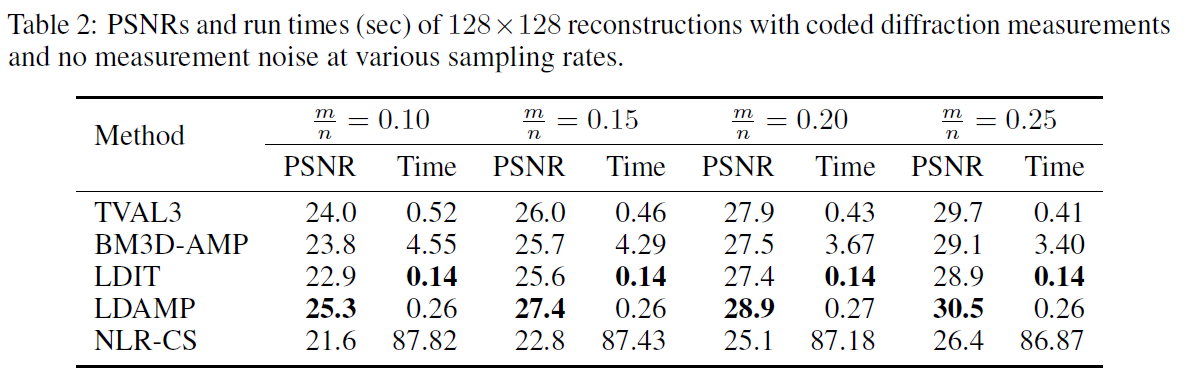
​ 编码衍射测量：在无噪的编码衍射测量情况下，LDAMP网络在除了指纹的每一个图像上都得到了最好的重构。在编码衍射测量情况下，LDIT和LDAMP产生的重构信号比其他方法快的多。注意，因为编码衍射测量的前向和后向操作均需要\(O(nlogn)\)阶操作，去噪变成了计算的主要来源：LDAMP比LDIT多了两倍的去噪操作，运行时间大约也需要两倍长。平均恢复PSNRs和运行时间在表2中展示。最后，我们比较了TVAL3，BM3D-AMP和LDAMP三种算法在512x512恢复的视觉比较。

6. 结论

​ 本文中，我们开发，分析，验证了一种新的神经网络结构来模仿功能强大的D-AMP信号恢复算法的行为。LDAMP网络易于训练，可应用于多种不同的测量矩阵，并有状态启发式来精确预测其性能。最重要的是LDAMP在精度和运行时间上都比先进算法BM3D-AMP和NLR-CS的性能更好。

​ LDAMP表达了在使用训练数据（和许多离线计算）来提高迭代算法性能的方向的最新示例。这篇文章背后的关键思想是，相比较于训练一个相对任意的黑匣子来学习恢复信号，我们可以展开传统的迭代算法将其结果视为一个神经网络，产生的网络行为易于理解，性能有保障，可预测网络缺点。我们希望可以对这个方法的突破带来益处，并鼓励该方向的进一步研究。