Luogu 1084 NOIP2012 疫情控制 (二分,贪心,倍增)
Luogu 1084 NOIP2012 疫情控制 (二分,贪心,倍增)
Description
H 国有 n 个城市,这 n 个城市用 n-1 条双向道路相互连通构成一棵树, 1 号城市是首都, 也是树中的根节点。
H 国的首都爆发了一种危害性极高的传染病。当局为了控制疫情,不让疫情扩散到边境 城市(叶子节点所表示的城市),决定动用军队在一些城市建立检查点,使得从首都到边境 城市的每一条路径上都至少有一个检查点,边境城市也可以建立检查点。但特别要注意的是, 首都是不能建立检查点的。
现在,在 H 国的一些城市中已经驻扎有军队,且一个城市可以驻扎多个军队。一支军队可以在有道路连接的城市间移动,并在除首都以外的任意一个城市建立检查点,且只能在 一个城市建立检查点。一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等 于道路的长度(单位:小时)。
请问最少需要多少个小时才能控制疫情。注意:不同的军队可以同时移动。
Input
第一行一个整数 n,表示城市个数。
接下来的 n-1 行,每行3个整数,u、v、w,每两个整数之间用一个空格隔开,表示从 城市 u 到城市v有一条长为w的道路。数据保证输入的是一棵树,且根节点编号为 1。
接下来一行一个整数 m,表示军队个数。
接下来一行 m 个整数,每两个整数之间用一个空格隔开,分别表示这 m 个军队所驻扎 的城市的编号。
Output
共一行,包含一个整数,表示控制疫情所需要的最少时间。如果无法控制疫情则输出-1。
Sample Input
4
1 2 1
1 3 2
3 4 3
2
2 2
Sample Output
3
Http
Luogu:https://www.luogu.org/problem/show?pid=1084
Source
二分,贪心,倍增
题目大意
给出一棵树,树上有若干个点有军队驻扎。现在求最小的军队行动时间使得军队移动使得从根1到任意一个儿子节点的路径上至少有一个军队把守
解决思路
首先考虑不可能的情况。我们定义根节点1的直属儿子为第一层,如果这个数据无解,当且仅当数据中的军队数小于第一层的点数,因为这样无论如何无法控制所有节点。而若时间无限的话,可以将所有军队调动到第一层,这样保证可以控制所有节点。
时间无限?这也就意味着一定存在一个时间点,使得在当前时间点及以后能够满足军队控制所有点,而再往前一点点就不行了。我们发现时间满足单调性
既然满足单调性,我们就二分时间,判断这个时间点是否可以让军队控制所有节点。
这个题最难的地方就是如何判断了(即check)
首先比较好想的是,在我们当前二分的时间\(mid\)下,所有的军队都是尽量向上跳,越上越好。因为是满足树的关系的,所以深度越浅,能控制的点就不会差。需要注意的是,这里需要提前处理好倍增数组,利用倍增加速跳的过程
接下来我们要把军队分为两部分,一部分是不管怎么跳都跳不到根节点1的,这些点就让它留在它能到的最浅的地方;另一部分是可以调到根节点1的,这也就意味着这些点可以通过1后到达第一层的其他点,控制1的其他子树,我们先把这些军队记录,同时存下这些军队剩余的时间和他的来源(指从它的出发点向上到达的第一层的点)。
然后我们首先来处理第一部分的点。对于一个点,如果它的儿子都已经被军队控制,那么它也相当于被军队控制,比如说这个例子:
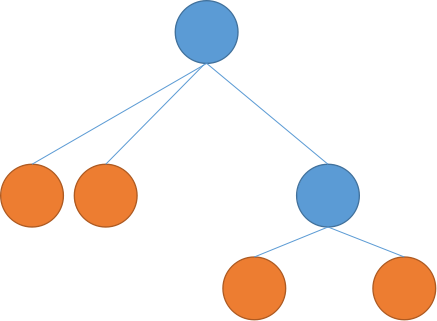
我们用橙色的点代表已经有军队控制的点,蓝色代表未控制。那么此时,两个蓝色点其实相对的也是被控制了的。这个过程我们可以用一个dfs来完成。
然后就是处理能到达1的军队。首先贪心的想一想,如果我们要让一个军队经过1到达另外一棵子树,我们只让它到第一层就可以了。所以,我们将所有军队按照剩余时间排序,将所有当前还未控制的第一层的点按照距离1的距离排序。贪心地让剩余时间最少的军队匹配能匹配的最大的。这里需要注意的是,如果我们枚举到一个军队时,发现它的来源还没有被控制,那么让它去控制它的来源。因为这意味着这个军队的来源在排序拍在后面,有可能无法匹配,而我们让这个军队撤回去一定会更优。
另外需要注意的是,这道题有一个很容易犯的错误,就是在标记出能到达1的军队后,先检查这些军队的来源有没有控制,如果没有就让剩余时间最小的来控制,这个贪心的是错误的,具体请看下面这个例子:
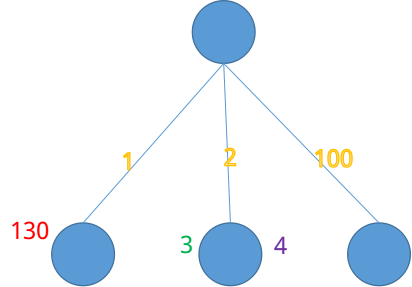
黄色的是边权,红色绿色和紫色的分别代表三只军队和剩余的时间。所有的点现在都没有控制。如果我们按照上面的贪心算法,先让军队去匹配它的来源,那么就是这样:
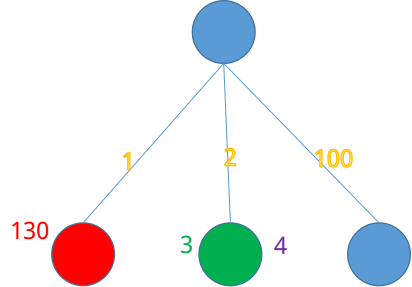
我们发现最右边的点没有被控制,那么是否意味着这是不可行的呢?
不,我们有这种走法:
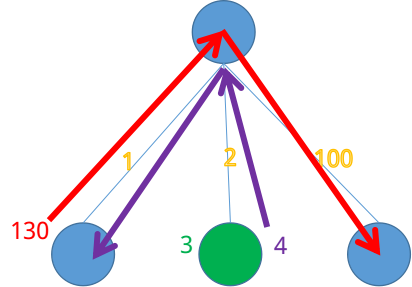
这样走,三个点都可以控制,所以,那种贪心方法是不正确的。
代码
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define ll long long
#define mem(Arr,x) memset(Arr,x,sizeof(Arr))
const int maxN=100001;
const int maxTwo=20;
const ll inf=1e15;
class Edge//边,前向星
{
public:
ll u,v,w;
};
class sort_data//用来排序的,这是在check中记录能到达根节点的点
{
public:
ll pos,resttime;//来源(第一层的点),剩余时间
};
bool operator < (sort_data A,sort_data B)//因为要排序,所以重载小于运算符
{
return A.resttime<B.resttime;
}
class Destination//记录还没有控制的第一层的点,同时记录它与1的距离
{
public:
ll pos,tim;//点编号,与1的距离
};
bool operator < (Destination A,Destination B)//重载小于运算
{
return A.tim<B.tim;
}
ll n,m;
int cnt;
ll Ans;//记录答案
int Head[maxN];//图
Edge E[maxN];//图
int Next[maxN];//图
ll Armypos[maxN];//记录每一个军队的初始所在点
ll Skip[25][maxN];//倍增数组,Skip[i][j]代表j号点向上跳2^j个点所到的位置
ll Skip_path[25][maxN];//倍增数组,Skip_path[i][j]代表对应的Skip[i][j]跳的距离
ll Getpos[maxN];//在check中记录每个军队向上跳最浅能跳到的点
bool is_cover[maxN];//在check中记录某个点是否已经被控制
ll read();
void Add_Edge(int u,int v,int w);//添加边
void Skip_dfs(int u,int father);//初始化倍增的信息
bool check(int mid);//二分检查
void check_dfs(int u,int father);//dfs检查,即这个用来处理把那些儿子都已经被控制的点也置为已控制
int main()
{
n=read();
cnt=0;
mem(Head,-1);
for (int i=1;i<n;i++)//读入树边
{
int u=read(),v=read(),w=read();
Add_Edge(u,v,w);
}
//开始构造倍增数组
mem(Skip,-1);
mem(Skip_path,0);
Skip_dfs(1,1);
for (int i=1;i<=maxTwo;i++)
for (int j=1;j<=n;j++)
if (Skip[i-1][j]!=-1)
{
Skip[i][j]=Skip[i-1][Skip[i-1][j]];
Skip_path[i][j]=Skip_path[i-1][j]+Skip_path[i-1][Skip[i-1][j]];
}
//构造完毕
m=read();//开始读入军队
for (int i=1;i<=m;i++)
Armypos[i]=read();
int l=0,r=300000;//二分
Ans=inf;
do
{
int mid=(l+r)/2;
if (check(mid))
{
Ans=min(Ans,(ll)(mid));
r=mid-1;
}
else
l=mid+1;
}
while (l<=r);
cout<<Ans<<endl;
return 0;
}
ll read()//快速读入
{
ll x=0;
char ch=getchar();
while ((ch>'9')||(ch<'0'))
ch=getchar();
while ((ch>='0')&&(ch<='9'))
{
x=x*10+ch-48;
ch=getchar();
}
return x;
}
void Add_Edge(int u,int v,int w)
{
cnt++;
Next[cnt]=Head[u];
Head[u]=cnt;
E[cnt].u=u;
E[cnt].v=v;
E[cnt].w=w;
cnt++;
Next[cnt]=Head[v];
Head[v]=cnt;
E[cnt].u=v;
E[cnt].v=u;
E[cnt].w=w;
return;
}
void Skip_dfs(int u,int father)//构造倍增初始数据,即Skip[0][i]和Skip_path[0][i]
{
for (int i=Head[u];i!=-1;i=Next[i])
{
int v=E[i].v;
if (v==father)
continue;
if (Skip[0][v]==-1)
{
Skip[0][v]=u;
Skip_path[0][v]=E[i].w;
Skip_dfs(v,u);
}
}
return;
}
bool check(int mid)//二分检查
{
mem(is_cover,0);
vector<sort_data> V;//记录能到达1的军队
V.clear();
for (int i=1;i<=m;i++)//让每一个军队都尽量向上跳
{
Getpos[i]=Armypos[i];//初始位置就是军队所在的位置
ll timecnt=0;//记录当前已花的时间
for (int j=maxTwo;j>=0;j--)
if ((Skip[j][Getpos[i]]>1)&&(timecnt+Skip_path[j][Getpos[i]]<=mid))//注意这里>1,
{
timecnt=timecnt+Skip_path[j][Getpos[i]];
Getpos[i]=Skip[j][Getpos[i]];
}
if ((Skip[0][Getpos[i]]==1)&&(Skip_path[0][Getpos[i]]+timecnt<mid))//当还能向上跳一次并且跳到1时,记录
{
V.push_back((sort_data){Getpos[i],mid-timecnt-Skip_path[0][Getpos[i]]});
}
else//否则则停在这里,直接控制这课子树
is_cover[Getpos[i]]=1;
}
check_dfs(1,1);//dfs检查控制
sort(V.begin(),V.end());//对剩余军队按剩余时间升序排序
vector<Destination> D;//记录还没有被控制的第一层节点
D.clear();
for (int i=Head[1];i!=-1;i=Next[i])
{
int v=E[i].v;
if (is_cover[v]==0)
D.push_back((Destination){v,E[i].w});
}
sort(D.begin(),D.end());//排序第一层点
if (D.size()>V.size())//当剩余军队数小于剩余第一层点数时,不管怎么呢调派军队都无法满足,返回不可行
return 0;
int j=0;//记录当前匹配到第几个点
if (D.size()==0)//若所有第一层点都已匹配,返回可行
return 1;
for (int i=0;i<V.size();i++)//i从小到大枚举每一个军队
{
if (is_cover[V[i].pos]==0)//若当前军队的来源还未控制,则让这支军队直接控制其来源,这样更划算
{
is_cover[V[i].pos]=1;
continue;
}
while ((is_cover[D[j].pos]==1)&&(j<D.size()))//因为有上面这种操作,所以先要让j跳到第一个还未匹配的第一层节点
j++;
if (j==D.size())//当j到末尾时,返回可行
return 1;
if (V[i].resttime>=D[j].tim)//判断当前军队是否可以去控制这个点,如果可以,则去控制
{
is_cover[D[j].pos]=1;
j++;
}
if (j==D.size())
return 1;
}
while ((is_cover[D[j].pos]==1)&&(j<D.size()))//最后再让j向后跳一次
j++;
if (j==D.size())//当到末尾时,返回可行
return 1;
return 0;//否则返回不可行
}
void check_dfs(int u,int father)
{
if (is_cover[u]==1)//已经被控制,直接返回
return;
bool is_all=1;//记录是不是所有的儿子都已经控制
bool has_son=0;//记录是否有儿子
for (int i=Head[u];i!=-1;i=Next[i])
{
int v=E[i].v;
if (v==father)
continue;
has_son=1;
check_dfs(v,u);
if (is_cover[v]==0)
is_all=0;
}
if (has_son==0)//当没有儿子时,肯定没有被控制
is_all=0;
if (is_all==1)//若所有儿子都被控制,则当前也标记为被控制
is_cover[u]=1;
return;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号