Luogu 1081 【NOIP2012】开车旅行 (链表,倍增)
Luogu 1081 【NOIP2012】开车旅行 (链表,倍增)
Description
小A 和小B决定利用假期外出旅行,他们将想去的城市从1到N 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i的海拔高度为Hi,城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即d[i, j] = |Hi − Hj|。
旅行过程中,小A 和小B轮流开车,第一天小A 开车,之后每天轮换一次。他们计划选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小B的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出X公里,他们就会结束旅行。
在启程之前,小A 想知道两个问题:
1.对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小(如果小 B的行驶路程为0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小A 开车行驶的路程总数与小B行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2.对任意给定的 X=Xi和出发城市 Si,小 A 开车行驶的路程总数以及小 B 行驶的路程总数。
Input
第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海拔高度,即H1,H2,……,Hn,且每个Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定M组Si和 Xi。
接下来的M行,每行包含2个整数Si和Xi,表示从城市 Si出发,最多行驶Xi公里。
Output
输出共M+1 行。
第一行包含一个整数S0,表示对于给定的X0,从编号为S0的城市出发,小A开车行驶的路程总数与小B行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和Xi下小A行驶的里程总数和小B 行驶的里程总数。
Sample Input
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3
Sample Output
1
1 1
2 0
0 0
0 0
Http
Luogu:https://www.luogu.org/problem/show?pid=1081
Source
链表,倍增
解决思路
首先分析一下题目,最朴素的想法就是每一次模拟小A和小B走的方式:小A走第二近的,小B走最近的,直到不能走为止。
那么我们每一次走都要找出最小差和次小差,所以我们考虑能否预处理出这个东西呢?即我们想预处理出从任意一个城市i出发,小A下一个走到的是哪一个城市,小B下一个走到的是哪一个城市。
所以我们先不考虑只能由标号小向编号大的走的情况,距离一个城市最近和次近的城市,一定在将所有城市排好序后,该城市前面两个和后面两个中小的两个。就像下面这样
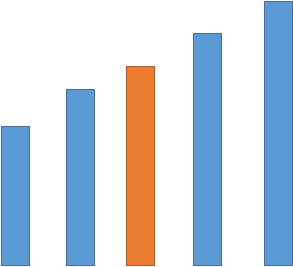
距离橘色代表的城市最近和次近的城市一定在这四个蓝色的城市中(按照海拔排序)
然后我们再考虑只能向右走。因为只能向右走,所以我们按原来输入的顺序从左向右依次扫描每一个城市,每次找出它再排序顺序中的前驱、前驱的前驱、后继和后继的后继,从这四个中选出最小和次小,然后将这个城市从排序序列中删除。这样做,就保证了一个城市只能走到其右边的城市。
我们如何维护这个东西呢?考虑到它需要快速的删除和求前驱和后继,我们可以用双向链表来支持这些操作。具体实现时,需要注意前驱或后继不存在的情况,避免非法访问。
这样我们就构造出了在任意一个城市,小A和小B各自下一个走到的城市。
这时我们如果将小A的走向或者小B的走向或者小A走一步小B再走一步,这三种方式分别画出来,我们发现它构成了类似树的结构。于是题目就转化成为在、从这棵树上的某一点出发,向上走尽可能长的距离同时满足这个距离不超过给定的X。
想到树上的距离,再结合现在算法的瓶颈————如何走,我们可以想到用倍增来加速走的过程。因为小A和小B是轮流走的,所以我们这里考虑将小A和小B各走一次称为一轮,我们对这个一轮进行倍增。构造出\(Skip\)跳转数组和小A和小B各自走的距离,我们定义\(Skip[i][j]\)表示从城市\(j\)出发走\(2^i\)轮走到的城市,同时用\(Skip\_A[i][j]和Skip\_B[i][j]\)记录小A与小B分别走的距离。
那么\(Skip[0][j],Skip\_A[0][j],Skip\_B[0][j]\)就是我们上面通过双向链表求出的东西,将这个作为初始值,我们来构造后面的跳转。
根据\(2^i=2*2^{i-1}\),我们可以得到
同理可得
同时注意,当这个倍增不能进行的时候,还需要判断小A能否再单独走一次,因为最后可能不满足让小A和小B都开一次,而只能让小A单独开一次。
有了上面的倍增数组,接下来我们来考虑如何对给出的问题求解。
对于第一问,求出对于给定的X,找出一个出发城市使得小A走的路程与小B走的路程的比值最小。这一问可以直接枚举每一个城市出发,倍增出小A的和小B的,求比值取最小即可。注意这里要特别关注小B走的为0的情况,此时如果直接除会出错,要跳过这种情况。
对于第二问,给出m组出发地和X,求A和B分别走的路程,直接倍增得出解即可。
代码
/*
经@gzy_HNoier指正,以下代码无法解决所有城市都只能让A走一步的情况,待更新
*/
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxN=100011;
const int maxTwo=20;
const int inf=2147483647;
class HEIGHT//这个class用于排序城市海拔,同时记录排序前的原编号,排序后的前驱和后继
{
public:
int h,num;//海拔,原编号
int nex,pre;//前驱,后继
};
bool operator < (HEIGHT A,HEIGHT B)//因为要支持排序,所以重载<运算符
{
return A.h<B.h;
}
int n,X;//n个城市,限定行驶距离为X
int Height[maxN];//城市海拔
HEIGHT Hclass[maxN];//排序后的城市海拔
int New_bh[maxN];//排序后,原来的每一个城市对应的新的编号
int Next_A[maxN];//从任意一个城市出发,小A走一次走到的城市
int Path_A[maxN];//从任意一个城市出发,小A走一次的距离,和上面对应
int Next_B[maxN];//从任意一个城市出发,小B走一次走到的城市
int Path_B[maxN];//从任意一个城市出发,小A走一次的距离,和上面对应
int Skip[23][maxN];//就是前面提到的跳转表
int Skip_A[23][maxN];//小A走的距离
int Skip_B[23][maxN];//小B走的距离
int read();
void Update(int &m1,int &m2,int h,int &id1,int &id2,int city);//这里是为了方便取最小值和次小值定义的函数,m1和m2分别是最小值和次小值,h为当前要比对的海拔差,id1和id2分别是最小值对应的城市,次小值对应的城市,city是当前用于对比的城市
int main()
{
n=read();
for (int i=1;i<=n;i++)//输入
{
Height[i]=read();
Hclass[i].h=Height[i];
Hclass[i].num=i;
}
sort(&Hclass[1],&Hclass[n+1]);//按海拔高度排序
for (int i=1;i<=n;i++)//初始化前驱和后继,同时将原来的编号和新编号对应起来
{
Hclass[i].pre=i-1;
Hclass[i].nex=i+1;
New_bh[Hclass[i].num]=i;
}
Hclass[1].pre=-1;//最前面和最后面的特殊置
Hclass[n].nex=-1;
for (int i=1;i<=n;i++)
{
int now=New_bh[i];//now即原第i个城市在排序中所在的位置
int m1=inf,m2=inf,h;//m1,m2分别为最小值,次小值,h为海拔差
int id1=-1,id2=-1;//分别记录最小值和次小值对应的城市编号,注意是原编号(不是排序的编号)
if (Hclass[now].pre!=-1)//查找前驱,这里每一次链表跳转都要判断是否存在
{
h=Hclass[Hclass[now].pre].h-Hclass[now].h;//注意这里没有加绝对值,因为根据题目对距离的定义,如果绝对值相等则海拔低的更近,所以我们把这个放在Update里面计算
Update(m1,m2,h,id1,id2,Hclass[now].pre);
int p=Hclass[now].pre;//查找前驱的前驱
if (Hclass[p].pre!=-1)//同样需要判断是否存在
{
h=Hclass[Hclass[p].pre].h-Hclass[now].h;//注意是与now的height而不是p的height
Update(m1,m2,h,id1,id2,Hclass[p].pre);
}
Hclass[p].nex=Hclass[now].nex;//更新前驱的后继,让它指向now的后继
}
if (Hclass[now].nex!=-1)//查找后继
{
h=Hclass[Hclass[now].nex].h-Hclass[now].h;
Update(m1,m2,h,id1,id2,Hclass[now].nex);
int nx=Hclass[now].nex;
if (Hclass[nx].nex!=-1)//查找后继的后继
{
h=Hclass[Hclass[nx].nex].h-Hclass[now].h;
Update(m1,m2,h,id1,id2,Hclass[nx].nex);
}
Hclass[nx].pre=Hclass[now].pre;//更新后继的前驱,让它指向now的前驱。这个操作和上面那个一起就可以达到再链表中删除now的目的。
}
Next_A[i]=Next_B[i]=-1;//因为可能不存在最小或次小,所以先置为不存在
Path_A[i]=Path_B[i]=0;
if (id1==-1)//当最小不存在时直接进行下一次操作
continue;
Next_B[i]=id1;//记录最小,即小B走的路
Path_B[i]=m1;
if (id2==-1)//当次小不存在时直接进行下一次操作
continue;
Next_A[i]=id2;//记录次小,即小A走的路
Path_A[i]=m2;
}
memset(Skip,-1,sizeof(Skip));//开始构造倍增表,-1表示不存在
for (int i=1;i<=n;i++)
{
if (Next_A[i]==-1)//如果小A不能走,则进入下一次计算
continue;
int nxa=Next_A[i];
if (Next_B[nxa]==-1)//注意这里是小B在小A的基础上走
continue;
Skip[0][i]=Next_B[nxa];//记录Skip的初始信息
Skip_A[0][i]=Path_A[i];
Skip_B[0][i]=Path_B[nxa];
}
for (int i=1;i<=maxTwo;i++)//通过上面的信息构造后面的
for (int j=1;j<=n;j++)
if (Skip[i-1][j]==-1)
continue;
else
{
Skip[i][j]=Skip[i-1][Skip[i-1][j]];
Skip_A[i][j]=Skip_A[i-1][j]+Skip_A[i-1][Skip[i-1][j]];
Skip_B[i][j]=Skip_B[i-1][j]+Skip_B[i-1][Skip[i-1][j]];
}
X=read();//开始求解第一问
int id;
double sol=inf;
for (int i=1;i<=n;i++)//枚举每一个城市
{
int pA=0,pB=0;//小A走的距离,小B走的距离
int ii=i;//当前走到哪个城市
for (int j=maxTwo;j>=0;j--)//倍增跳转
if (Skip[j][ii]!=-1)//注意可行时才可以跳
if (Skip_A[j][ii]+Skip_B[j][ii]+pA+pB<=X)
{
pA+=Skip_A[j][ii];//走2^j轮
pB+=Skip_B[j][ii];
ii=Skip[j][ii];
}
if ((Next_A[ii]!=-1)&&(Path_A[ii]+pA+pB<=X))//若小A还可以再走,则让小A单独走一次
{
pA+=Path_A[ii];
ii=Next_A[ii];
}
if (pB==0)//注意这里小B没有走的时候要跳过
continue;
if (1.0*pA/pB<sol)
{
sol=1.0*pA/pB;
id=i;
}
}
printf("%d\n",id);
int M=read();//求解第二问
while (M--)
{
int st=read();
X=read();
int pA=0,pB=0;//小A走的距离,小B走的距离
for (int j=maxTwo;j>=0;j--)
if (Skip[j][st]!=-1)
if (Skip_A[j][st]+Skip_B[j][st]+pA+pB<=X)
{
pA+=Skip_A[j][st];
pB+=Skip_B[j][st];
st=Skip[j][st];
}
if ((Next_A[st]!=-1)&&(Path_A[st]+pA+pB<=X))//让小A再走一次
{
pA+=Path_A[st];
st=Next_A[st];
}
printf("%d %d\n",pA,pB);
}
return 0;
}
int read()//数据比较多,优化读入
{
int x=0,k=1;
char ch=getchar();
while (((ch>'9')||(ch<'0'))&&(ch!='-'))
ch=getchar();
if (ch=='-')
{
k=-1;
ch=getchar();
}
while ((ch>='0')&&(ch<='9'))
{
x=x*10+ch-48;
ch=getchar();
}
return x*k;
}
void Update(int &m1,int &m2,int h,int &id1,int &id2,int city)//更新最小值和次小值
{
city=Hclass[city].num;//注意传进来的city是在排序数组中的编号,要转变成为原来输入的编号
int h2=abs(h);//h2记录绝对值距离
if ((h2<m1)||((h2==m1)&&(h<0)))//注意题目中距离的定义,若距离相等时,海拔小的更近
{
m2=m1;
m1=h2;
id2=id1;
id1=city;
}
else
if ((h2<m2)||((h2==m2)&&(h<0)))//这里同样
{
m2=h2;
id2=city;
}
return;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号