KMP算法（研究总结，字符串）

KMP算法（研究总结，字符串）

前段时间学习KMP算法，感觉有些复杂，不过好歹是弄懂啦，简单地记录一下，方便以后自己回忆。

引入

首先我们来看一个例子，现在有两个字符串A和B，问你在A中是否有B，有几个？为了方便叙述，我们先给定两个字符串的值
A="abcaabababaa"
B="abab"
那么普通的匹配是怎么操作的呢？
当然就是一位一位地比啦。（下面用蓝色表示已经匹配，黑色表示匹配失败）

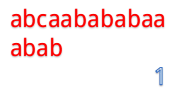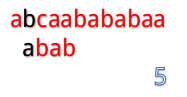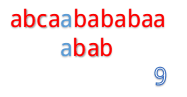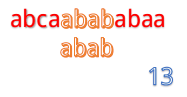
但是我们发现这样匹配很浪费!
为什么这么说呢，我们看到第4步：

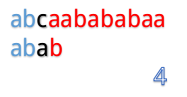
在第4步的时候，我们发现第3位上c与a不匹配，然后第五步的时候我们把B串向后移一位，再从第一个开始匹配。

这里就有一个对已知信息很大的浪费，因为根据前面的匹配结果，我们知道B串的前两位是ab，所以不管怎么移，都是不能和b匹配的,所以应该直接跳过对A串第二位的匹配，对于A串的第三位也是同理。

或许这这个例子还不够经典，我们再举一个。

A="abbaabbbabaa"
B="abbaaba"

在这个例子中，我们依然从第1位开始匹配，直到匹配失败：

abbaabbbabba
abbaaba
我们发现第7位不匹配
那么我们若按照原来的方式继续匹配，则是把B串向后移一位，重新从第一个字符开始匹配
abbaabbbabba
_abbaaba
依然不匹配，那我们就要继续往后移咯。
且住！
既然我们已经匹配了前面的6位，那么我们也就知道了A串这6位和B串的前6位是匹配的，我们能否利用这个信息来优化我们的匹配呢？
也就是说，我们能不能在上面匹配失败后直接跳到：
abbaabbbabba
____abbaaba
这样就可以省去很多不必要的匹配。

KMP算法

KMP算法就是解决上面的问题的，在讲述之前，我们先摆出两个概念：

前缀：指的是字符串的子串中从原串最前面开始的子串，如abcdef的前缀有：a,ab,abc,abcd,abcde
后缀：指的是字符串的子串中在原串结尾处结尾的子串，如abcdef的后缀有：f,ef,def,cdef,bcdef

KMP算法引入了一个F数组（在很多文章中会称为next,但笔者更习惯用F，这更方便表达），F[i]表示的是前i的字符组成的这个子串最长的相同前缀后缀的长度！
怎么理解呢？
例如字符串aababaaba的相同前缀后缀有a和aaba，那么其中最长的就是aaba。

KMP算法的难理解之处与本文叙述的约定

在继续我们的讲述之前，笔者首先讲一下为什么KMP算法不是很好理解。
虽然说网上关于KMP算法的博客、教程很多，但笔者查阅很多资料，详细讲述过程及原理的不多，真正讲得好的文章在定义方面又有细微的不同（当然，真正写得好的文章也有，这里就不一一列举），比如说有些从1开始标号，有些next表示的是前一个而有些是当前的，通读下来，难免会混乱。
那么，为了防止读者在接下来的内容中感到和笔者之前学习时同样的困惑，在这里先对下文做一些说明和约定。

1.本文中，所有的字符串从0开始编号
2.本文中，F数组（即其他文章中的next），F[i]表示0~i的字符串的最长相同前缀后缀的长度。

F数组的运用

那么现在假设我们已经得到了F的所有值，我们如何利用F数组求解呢？
我们还是先给出一个例子（笔者用了好长时间才构造出这一个比较典型的例子啊）：
A="abaabaabbabaaabaabbabaab"
B="abaabbabaab"
当然读者可以通过手动模拟得出只有一个地方匹配
abaabaabbabaaabaabbabaab
那么我们根据手动模拟，同样可以计算出各个F的值

B="a b a a b b a b a a b "
F= 0 0 1 1 2 0 1 2 3 4 5（2017.7.25 Update 这里之前有一个错误，感谢@ 歌古道指正）（2017.7.29 Update 好吧，这里原来还有一个错误，已经更正啦感谢@iwangtst）

我们再用i表示当前A串要匹配的位置（即还未匹配），j表示当前B串匹配的位置（同样也是还未匹配），补充一下，若i>0则说明i-1是已经匹配的啦（j同理）。
首先我们还是从0开始匹配：

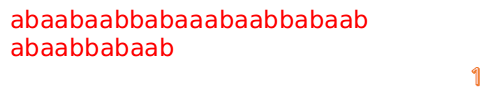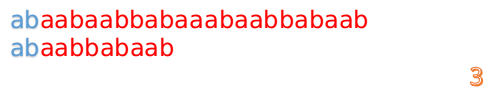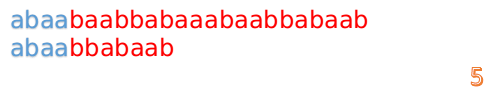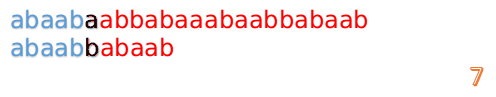
此时，我们发现，A的第5位和B的第5位不匹配（注意从０开始编号），此时i=5,j=5，那么我们看F[j-1]的值：

F[5-1]=2;

这说明我们接下来的匹配只要从B串第２位开始（也就是第３个字符）匹配，因为前两位已经是匹配的啦，具体请看图：

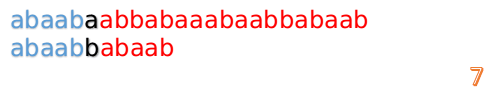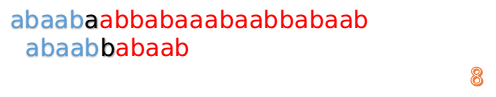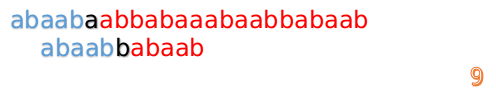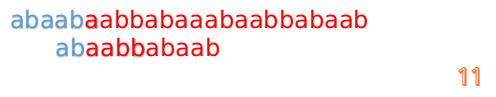
然后再接着匹配：

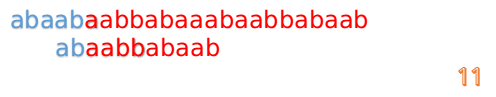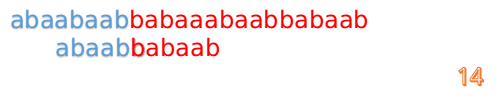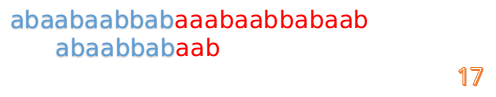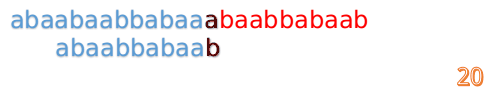
我们又发现，A串的第13位和B串的第10位不匹配，此时i=13,j=10，那么我们看F[j-1]的值：

F[10-1]=4

这说明B串的0_{3位是与当前(i-4)}(i-1)是匹配的，我们就不需要重新再匹配这部分了，把B串向后移，从Ｂ串的第４位开始匹配：

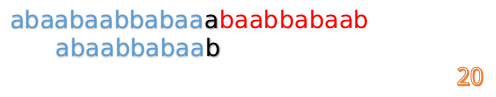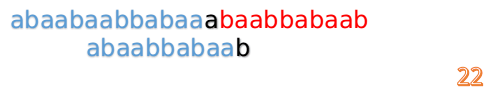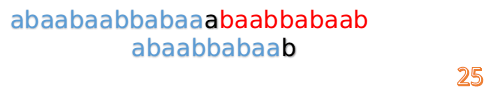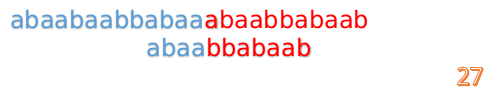
这时我们发现A串的第13位和B串的第4位依然不匹配

此时i=13,j=4，那么我们看F[j-1]的值：

F[4-1]=1

这说明B串的第0位是与当前i-1位匹配的，所以我们直接从B串的第1位继续匹配：

但此时B串的第1位与A串的第13位依然不匹配

此时，i=13,j=1,所以我们看一看F[j-1]的值:

F[1-1]=0

好吧，这说明已经没有相同的前后缀了，直接把B串向后移一位，直到发现B串的第0位与A串的第i位可以匹配（在这个例子中，i=13）

再重复上面的匹配过程，我们发现，匹配成功了！

这就是KMP算法的过程。
另外强调一点，当我们将B串向后移的过程其实就是i++,而当我们不动B，而是匹配的时候，就是i++,j++，这在后面的代码中会出现，这里先做一个说明。

最后来一个完整版的（话说做这些图做了好久啊！！！！）：

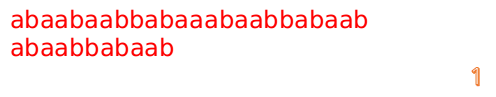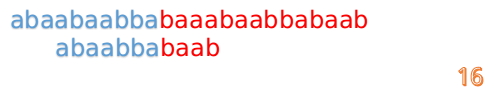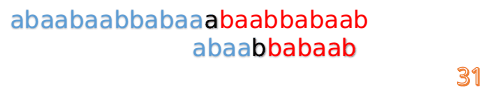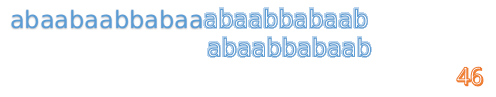
F数组的求解

既然已经用这么多篇幅具体阐述了如何利用F数组求解，那么如何计算出F数组呢？总不能暴力求解吧。

KMP的另外一个巧妙的地方也就在这里，它利用我们上面用B匹配A的方法来计算F数组，简单点来说，就是用B串匹配B串自己！
当然，因为B串==B串，所以如果直接按上面的匹配，那是毫无意义的（自己当然可以完全匹配自己啦），所以这里要变一变。

因为上面已经讲过一部分了，先给出计算F的代码：

for (int i=1;i<m;i++)
{
    int j=F[i-1];
    while ((B[j+1]!=B[i])&&(j>=0))
        j=F[j];
    if (B[j+1]==B[i])
        F[i]=j+1;
    else
        F[i]=-1;
}

首先可以确定的几点是：

1.F[0]=-1　(虽说这里应该是０，但为了方便判越界，同时为了方便判断第０位与第i位，程序中这里置为-1)
2.这是一个从前往后的线性推导，所以在计算F[i]时可以保证F[0]~F[i-1]都是已经计算出来的了
3.若以某一位结尾的子串不存在相同的前缀和后缀，这个位的F置为-1（这里置为-1的原因同第一条一样）

重要！：另外，为了在程序中表示方便，在接下来的说明中，F[i]=0表示最长相同前缀后缀长度为１，即真实的最长相同前缀后缀＝F[i]+1。(重要的内容要放大)
为什么要这样设置呢，因为这时F[i]代表的就不仅仅与前后缀长度有关了，它还代表着这个前缀的最后一个字符在子串B中的位置。

所以，之前上面列出的F值要变一下（这里用'_'辅助对齐）：

B="a _b a a b _b a b a a b "
F= -1 -1 0 0 1 -1 0 1 2 3 4

那么，我们同样可以推出，求解F的思路是：看F[i-1]这个最长相同前缀后缀的后面是否可以接i，若可以，则直接接上，若不可以，下面再说。
举个例子：
还是以B="abaabbabaab"为例，我们看到第2个。

B="a b a a b b a b a a b"
F=-1 -1

此时这个a的前一个b的F值为-1，所以此时a不能接在b的后面（b的相同最长前缀后缀是０啊），此时，j=-1，所以我们判断B[j+1]与B[2]，即B[0]与B[2]是否一样。一样，所以F[2]=j+1=0（代表前0~2字符的最长相同前缀后缀的前缀结束处是B[0],长度为0+1=1）。

再来看到第３个：

B="a b a a b b a b a a b"
F=-1 -1 0

开始时,j=F[3-1]=0，我们发现B[j+1=1]!=B[i=3]，所以j=F[j]=-1,此时B[j+1=0]==B[i=3]，所以F[3]=j+1=0。

最后举个例子，看到第４个

B="a b a a b b a b a a b"
F=-1 -1 0 0

j首先为F[4-1]=0，我们看到B[j+1=1]==B[i]，所以F[i]=j+1=1。

后面的就请读者自己慢慢推导了。再强调一遍，我们这样求出来的F值是该最长相同前缀后缀中的前缀的结束字符的数组位置（从０开始编号），如果要求最长相同前缀后缀的长度，要输出F[i]+1。

代码

求解F数组：

for (int i=1;i<m;i++)
{
    int j=F[i-1];
    while ((B[j+1]!=B[i])&&(j>=0))
        j=F[j];
    if (B[j+1]==B[i])
        F[i]=j+1;
    else
        F[i]=-1;
}

利用F数组寻找匹配，这里我们是每找到一个匹配就输出其开始的位置：

while (i<n)
{
    if (A[i]==B[j])
    {
        i++;
        j++;
        if (j==m)
        {
            printf("%d\n",i-m+1);//注意,这里输出的位置是从1开始标号的,如果你要输出从0开始标号的位置,应该是是i-m.这份代码是我做一道题时写的,那道题要求输出的字符串位置从1开始标号.感谢@Draymonder指出了这个疏漏,更多内容请看评论区
            j=F[j-1]+1;
        }
    }
    else
    {
        if (j==0)
            i++;
        else
            j=F[j-1]+1;
    }
}

以下内容 Update at 2019.4.26

贴一个现在自己的写法，不过这里字符串是从 1 开始标号的，如果上面理解了的话不难转化。

Nxt[0]=Nxt[1]=0;
for (int i=2,j=0;i<=m;i++){//构建 Next
    while (j&&T[j+1]!=T[i]) j=Nxt[j];
    if (T[j+1]==T[i]) ++j;Nxt[i]=j;
}
for (int i=1,j=0;i<=n;i++){//匹配
    while (j&&T[j+1]!=S[i]) j=Nxt[j];
    if (T[j+1]==S[i]) ++j;
    if (j==m) Mch[i]=1,j=Nxt[j];//匹配成功
}