BZOJ 2693 jzptab 【莫比乌斯反演】

Description

Hint

T <= 10000
N, M<=10000000

Solution

和 BZOJ 2154 数字表格 几乎一样，只不过询问变成多组，之前的复杂度又过不了了

依旧写开答案

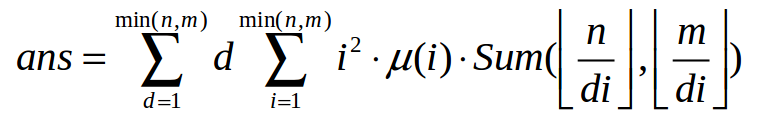
又有两个枚举量

我们尝试改变求和指标+前缀和继续减掉一个枚举量

于是就有了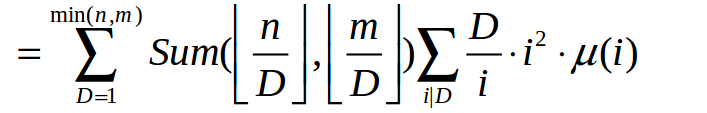

对于这个东西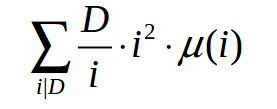我们定义它为 h ( D )

使可以进行前缀和预处理的

考虑枚举 i 和 i 的倍数

然而这样的处理显然也是接受不了的

似乎只有O(n)的复杂度才可能接受

能不能把 h 放到线性筛之中处理出来呢

对于一个素数p，它的新 h 值显然是 p - p^2 的

如果 p 是多个素数的一次项的积

显然 h 是积性的 h( p ) = h( p1 ) * h( p2 ) * h( p3 )……

如果 p 的唯一分解可以写成一部分素数乘积 i 与 另一部分在前一部分中出现过的素数的乘积 j，也就是存在质因子的指数大于1，它新增的每一个因子的 μ 值都是0，没有意义，只有统计时D变成了原来的 j 倍

所以 此时 h( p ) = h( i ) * j

前缀和在之后加一下就可以了

 1 #include<bits/stdc++.h>
 2 
 3 #define mod 100000009
 4 #define maxp 10000000
 5 #define maxn 10000000+5
 6 #define set(a,b) memset(a,(b),sizeof(a))
 7 #define fr(i,a,b) for(ll i=(a),_end_=(b);i<=_end_;i++)
 8 #define rf(i,b,a) for(ll i=(a),_end_=(b);i>=_end_;i--)
 9 #define fe(i,a,b) for(int i=first[(b)],_end_=(a);i!=_end_;i=s[i].next)
10 #define fec(i,a,b) for(int &i=cur[(b)],_end_=(a);i!=_end_;i=s[i].next)
11 
12 using namespace std;
13 
14 typedef long long ll;
15 
16 ll f[maxn],h[maxn];
17 ll ans;
18 int prime[maxn],pri[maxn],tot=0;
19 int n,m,T;
20 
21 void read()
22 {
23 #ifndef ONLINE_JUDGE
24   freopen("2693.in","r",stdin);
25   freopen("2693.out","w",stdout);
26 #endif
27   //cin >> T ;
28   scanf("%d",&T);
29 }
30 
31 void write()
32 {}
33 
34 void print()
35 {
36   //cout << ans << endl ;
37   printf("%lld\n",ans);
38 }
39 
40 void get()
41 {
42   h[1]=1;
43   fr(i,2,maxp){
44     if( !prime[i] ) pri[++tot]=i,h[i]=(i-i*i%mod)%mod;
45     int j=1;
46     while( j<=tot && pri[j]*i<=maxp ){
47       prime[ pri[j]*i ]=1;
48       if( i%pri[j]==0 ){
49     h[pri[j]*i]=pri[j]*h[i]%mod;
50     break;
51       }
52       h[pri[j]*i]=h[pri[j]]*h[i]%mod;
53       j++;
54     }
55   }
56   fr(i,1,maxp)
57     f[i]=(f[i-1]+h[i])%mod;
58 }
59 
60 ll Sum(ll x,ll y)
61 {
62   return ((x+1)*x/2%mod)*((y+1)*y/2%mod)%mod;
63 }
64 
65 
66 ll calc(ll x,ll y)
67 {
68   if( x>y ) swap(x,y);
69   ll res=0,i=1,pos;
70   while( i<=x ){
71     pos=min(x/(x/i),y/(y/i));
72     res=(res+Sum(x/i,y/i)*(f[pos]-f[i-1])%mod)%mod;
73     i=pos+1;
74   }
75   return (res+mod)%mod;
76 }
77 
78 void work()
79 {
80   get();
81   while( T-- ){
82     //cin >> n >> m ;
83     scanf("%d%d",&n,&m);
84     ans=calc(n,m);
85     print();
86   }
87 }
88 
89 int main()
90 {
91   read();
92   work();
93   write();
94   return 0;
95 }

 

posted @ 2015-07-02 21:56  ST_Saint  阅读(1385)  评论(0)  编辑  收藏  举报