CF1467C Three Bags
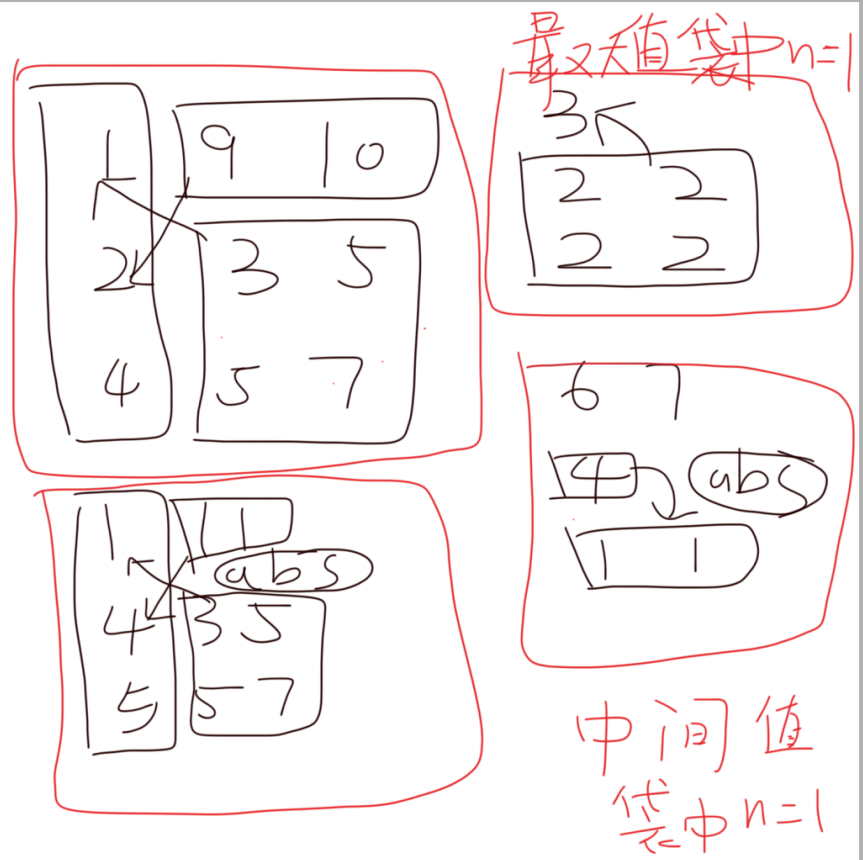
思路：对于一般情况，我们有三个袋子，容易想到把袋子里物品的价值排序。然后贪心，我们想让最后的价值最大，则三个袋子最后都可以剩余一个物品，这三个物品总和需要最大，最好的情况就是三个物品的符号“+”，“-”，“-”,这样总价值直接可以算是每个袋子中物品绝对值的累加和。为了让三个物品价值最大，我们可以容易想到，价值大的物品减去价值小的物品，让可用价值尽可能大，而且最后剩余每个袋子的最后物品符号分别是“+”“-”“-”。这样，我们之前每个袋子的物品都排好了序，容易想到，对于三个袋子中，每个袋子价值最小的物品是关键。因为我们需要让可用价值尽可能大，所以我们可以让三个袋子中，最小值最大的那个物品为“+”,然后让其他两个袋子中的最小物品收集其他价值，这样就满足了三个袋子都只剩下一个物品且满足“+”“-”“-”。我们可以让最小值最大和最小值中间大的袋子中其他物品累加减去和最小值最小的物品让其为“-”，然后让最小值最小的其他物品累加和减去最小值中间大的那个物品让其为“-”就可以了。但最小值最小的其他所有物品和最小值中间大的物品的差值会有特殊情况，例如：最小值的其他物品 1，1；中间值的最小值 4.这样（4-1-1 = 2）,这里需要特判一下，我们发现两者的差值只需要取一个abs就可以了，上面的例子可以转化为：1 - 中间值放入最小值的袋中，变成了abs（-3+1）。
然后就是特殊情况，即三个袋子中任意一个袋子的物品只有一个的情况，需要特殊判断。
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <cmath> 6 #include <queue> 7 #include <vector> 8 #include <cstring> 9 #include <functional> 10 #include <map> 11 #define LL long long 12 #define lson(rt) (rt << 1) 13 #define rson(rt) (rt << 1 | 1) 14 using namespace std; 15 16 const int N = 1e3 + 10; 17 struct node 18 { 19 int v, id; 20 21 bool friend operator<(const node& a, const node& b) 22 { 23 return a.v < b.v; 24 } 25 }; 26 int a[N]; 27 28 void solve () 29 { 30 int n, m, k, x; 31 scanf("%d%d%d", &n, &m, &k); 32 vector<int > a[3]; 33 for(int i = 0; i < n; ++i) { 34 35 scanf("%d", &x); 36 a[0].push_back(x); 37 } 38 for(int i = 0; i < m; ++i) { 39 scanf("%d", &x); 40 a[1].push_back(x); 41 } 42 for(int i = 0; i < k; ++i) { 43 scanf("%d", &x); 44 a[2].push_back(x); 45 } 46 for(int i = 0; i < 3; ++i) sort(a[i].begin(), a[i].end()); 47 48 vector<node > vn; 49 vn.push_back({a[0][0], 0}); 50 vn.push_back({a[1][0], 1}); 51 vn.push_back({a[2][0], 2}); 52 53 sort(vn.begin(), vn.end()); 54 55 56 int maxx = vn[2].id; 57 int midd = vn[1].id; 58 int minn = vn[0].id; 59 60 long long maxv, midv, minv; 61 maxv = midv = minv = 0; 62 for(auto x : a[maxx]) maxv += x; 63 for(auto x : a[midd]) midv += x; 64 for(auto x : a[minn]) minv += x; 65 // printf("(%lld %lld %lld)\n", maxv, midv,minv); 66 midv -= a[midd][0]; 67 minv -= a[minn][0]; 68 maxv -= a[maxx][0]; 69 // printf("(%lld %lld %lld)\n", maxv, midv,minv); 70 // printf("(%d %d %d)\n", a[maxx].size(), a[midd].size(), a[minn].size()); 71 long long ans = 0; 72 if(a[minn].size() == 1) { 73 ans += maxv + midv + a[maxx][0] + a[midd][0] - a[minn][0]; 74 } else if(a[midd].size() == 1) { 75 // cout << "s" << endl; 76 ans += abs(minv + a[minn][0] - a[midd][0]); 77 ans += a[maxx][0] + maxv; 78 } else if(a[maxx].size() == 1 && a[maxx][0] < a[midd][0] + a[minn][0]) { 79 ans += midv + minv + a[midd][0] + a[minn][0] - a[maxx][0]; 80 } else { 81 // cout << "s" << endl; 82 ans += a[maxx][0] + maxv + midv - a[minn][0]; 83 ans += abs(minv - a[midd][0]); 84 } 85 86 printf("%lld\n", ans); 87 } 88 89 int main () 90 { 91 92 solve(); 93 94 return 0; 95 }
1
