反素数解析

反素数的定义：

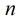
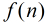
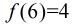
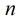
　对于任何正整数，其约数个数记为，例如，如果某个正整数满足：对任意的正整

   数，都有，那么称为反素数。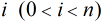

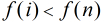
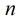
或者：             

    一个[1,n]的连续区间, 约数相同的最小数x，x是反素数。例如：f(6) = 4,f(8) = 4,6是约数为4切最小的数，所以6是约数。

 

反素数性质：

  1. 反素数肯定是从2开始的连续素数的幂次形式的乘积。
  2. 数值小的素数的幂次大于等于数值大的素数，即n = p_{1}^{k_{1}}*p_{2}^{k_{2}}*p_{3}^{k_{3}}*...*p_{n-1}^{k_{n-1}}*p_{n}^{k_{n}}中，有k_{1}\geq k_{2}\geq k_{3}\geq ...\geq k_{n}

 

性质的解析：

　　根据 反素数定义：

　　对于性质二： （5^6）*（7^2）*（11^7） > （5^7）*（7^6）*（11^2）

　　对于性质一：（5^7）*（7^6）*（11^2） > （2^7）*（3^6）*（5^2）

 

例题：反素数模板题

我们先求出这个区间最多由几个素数相乘，即n = p_{1}^{k_{1}}*p_{2}^{k_{2}}*p_{3}^{k_{3}}*...*p_{n-1}^{k_{n-1}}*p_{n}^{k_{n}}，(k1 = k2  = k3 = ... = kn , kn = 1)

我们再求出这个区间的最大数最多是最小素数的几次幂。 2e9 < 2^30。

 1 #include <iostream>
 2 #include <cstdio>
 3 #define ll long long
 4 
 5 using namespace std;
 6 
 7 int p[] = {2,3,5,7,11,13,17,19,23,29};
 8 int Max,ans,n; 
 9 //Max 最大约数个数  ans 反素数
10 
11 // inx 素数下标  v当前数值  cnt 约数个数  pw之前的幂次
12 void dfs(int inx, int v, int cnt, int pw){
13 
14     for(int i = 1; i <= pw; ++i){
15         if((ll)v * p[inx] > (ll)n){
16             if(Max < cnt * i){
17                 Max = cnt * i;
18                 ans = v;
19 
20             }else if(cnt * i == Max) ans = min(ans, v);
21             break;
22         }
23         else dfs(inx + 1, v *= p[inx], cnt * (i + 1), i);
24 
25     }
26 }
27 
28 
29 int main(){
30 
31     while(~scanf("%d", &n)){
32         Max = 1;
33         dfs(0, 1, 1, 30);
34         printf("%d\n", ans);
35     }
36 
37     return 0;
38 }

 

posted @ 2020-03-25 18:17  SummerMingQAQ  阅读(729)  评论(0)  编辑  收藏  举报