卷积

卷积和

理解卷积核心就是要理解自变量变换，卷积和的公式如下：

\[y[n]=\sum_{k=-\infty}^{+\infty}x[k]h[n-k] \\ ~\\ y[n]=x[k]*h[n-k] \]

这里重点是 \(h[n-k]\), 它是 \(h[n]\) 自变量 \(n\) 平移 \(k\) 后的函数。
卷积和定义了一个新的离散函数 \(y[n]\)，\(n, k\)是自变量坐标上不同的点。
当确定函数 \(x\) 的一个点 \(k\), 对应任意一点 \(n\), 有 \(n\) 与 \(k\) 之间的距离为 \(n-k\).
先看卷积和单项式的含义。假定 \(k\) 为定数，即在给定点 \(k\), 有函数:

\[r_k[n]=x[k]h[n-k] \]

函数 \(r_k[n]\) 为函数 \(x\) 在 \(k\) 点的值与函数 \(h[n-k]\)的乘积。重点考察函数 \(h[n-k]\), \(k\) 为常数，\(n\) 为自变量，宗量 \(n-k\) 为自变量 \(n\) 的变换函数。对于 \(x[k]\), 函数\(r_k[n]\)的另一个乘积项为函数\(h\)在宗量 \(n-k\) 上的取值，即 \(h[(n-k)-0]\)的值，即函数 \(h\) 从0偏移\(n\)与\(k\)的距离，这里既不是\(h[n]\)，也不是\(h[k]\),而是取\((n,k)\)的距离\(h[n-k]\)。可以认为，\(x[k]\)的值对函数\(r_k[n]\)在n点的影响与 \(n\) 与 \(k\) 的差值即距离相关，相关的方式是用差值\(n-k\)求得函数\(h[n-k]\)的值作为另一个乘积项。
那么，在给定的 \(k\) 点可得一个 \(n\) 点的函数值 \(r_k[n]\)，对任意 \(k\) 点都可得一个 \(r_k[n]\) 的值，所有k点的\(r_k[n]\) 值的累积和为：

\[\begin{aligned} \\ S[n] &= \sum_{k=-\infty}^{+\infty}r_k[n] \\ &= \sum_{k=-\infty}^{+\infty}x[k]h[n-k] \\ &=y[n] \end{aligned} \]

通过上面的分析，卷积和就是要求得一个函数\(y[n]\)，这个函数要求得在函数 \(x[n]\)及函数\(h[n]\)的定义域上任意一个\(n\)，在这个点映射出来的值，与\(x[n]\)的定义域上全部值域都有关系，也即在\(x[n]\)的定义域上的每个函数值都对函数\(y[n]\)在给定点\(n\)的函数值有关系,这种关系由\(x[n]\)上每个点\(k\)与\(y[n]\)与位于\(n\)点的自变量距离和另外一个给定函数\(h[n-k]\)决定，即取 \(h[n-k]\)值为函数的一个计算因子。
这样，卷积和的结果就是一个以卷积因子的全部值域为变量的函数。一个例子就是如果对一副图进行卷积运算，那么，原图上的每个点可以设置一个新的属性，新属性由原图的所有点运算得到，而这个点的新属性和该点与其他点的属性及距离有关，这个距离作为卷积运算中一个计算因子的因变量。
设\(P\)为图的点集，\(p(i), i \in P\)为点集中的点\(i\)的原属性，定义图上点的新属性\(N(i)\)：

\[N(j) = \sum_{i\in P}p[i]h[j-i] \]

式中函数 \(h\) 将决定新属性的意义，它对点 \(j\) 的新属性受其他点原属性的影响由卷积结果的 \(j\) 点与其他点的距离决定。
举例说明，如果原属性为图上点的亮度值，选择合适的函数\(h[i]\)，可生成锐化或钝化的黑白图像。参见如何通俗易懂地解释卷积。
卷积和的关键是对于每一个\(x[k]\)，确定其对\(y[n]\)贡献的\(h\)函数的宗量，简单的数学表达式就是 \(n-k\) ,其他方法的目的也是一样，只是从不同的角度去求这个值。
事实上，如果把 \(h[n-k]\) 视为 \(h[k]\) 经变换 \(f[j]=h[-(k-n)]\), 即反转后移位\(n\)后，\(x[k]h[n-k]=x[k]f[k]\), 即对 \(h\) 进行反转移位\(n\)后, n处的卷积和的各项因子在坐标上是对齐的，实际上对齐的\(f[k]\)的值就是\(h[n-k]\)的值。

卷积积分

用冲激函数表示连续函数

连续函数 \(x(t)\)可用阶梯函数近似表达：

设阶梯函数表示为 \(\hat{x}(t)\), \(\hat{x}(t)\)的步进为 \(\Delta\)。
定义脉冲函数\(\delta_{\Delta}(t)\)如下式：

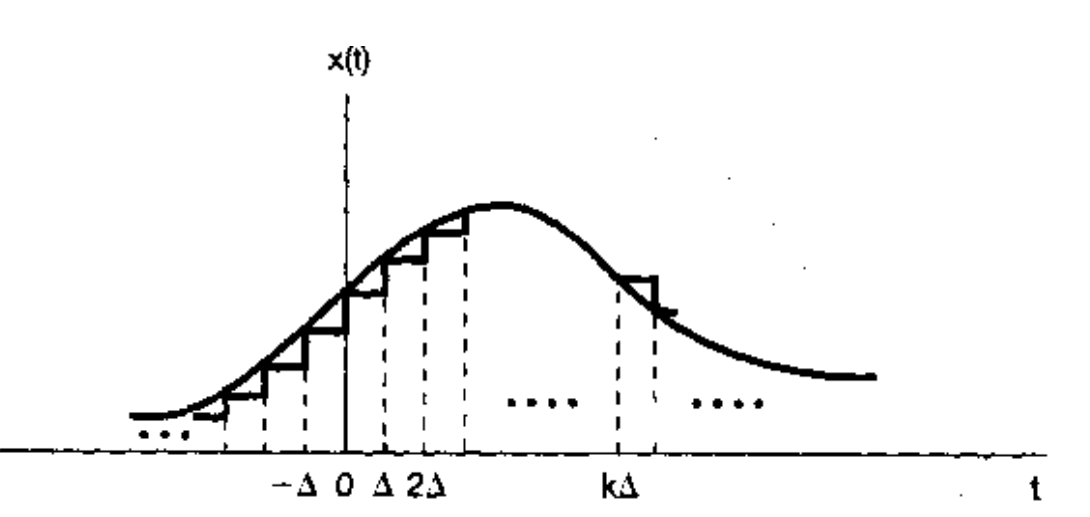
\[\delta_{\Delta}(t)=\left\{\begin{array}{lc} \frac{1}{\Delta}, & 0 \leqslant t \leqslant \Delta \\ 0, & \text { 其余 } t \end{array}\right. \]

这是一个位于\([0,\Delta]\)范围，高度为\(\frac{1}{\Delta}\)的一个脉冲函数。
阶梯函数的某一段\([k\Delta,k\Delta+\Delta]\)的函数\(\hat{x}_k(t)\)可用脉冲函数 \(\delta_{\Delta}(t)\)的移位函数 \(\delta_{\Delta}(t-k\Delta)\) 与\(x(k\Delta)\)及\(\Delta\)的乘积\(x(k\Delta)\delta_{\Delta}(t-k\Delta)\Delta\)来表示:

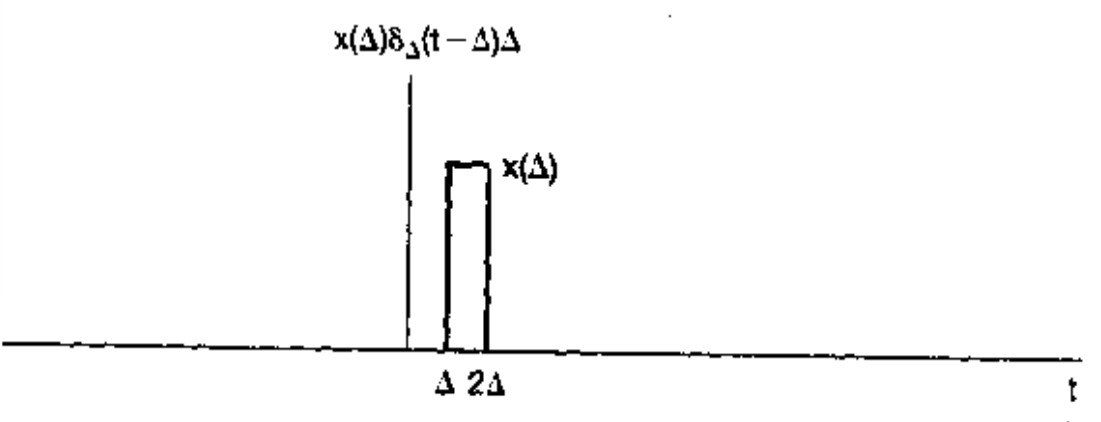
上图这一段为：

\[\hat{x}_k(t)=x(k\Delta)\delta_{\Delta}(t-k\Delta)\Delta \]

因为\(\delta_{\Delta}(t-k\Delta)\)的高度为 \(\frac{1}{\Delta}\), 且仅在 $k\Delta \leqslant t \leqslant k\Delta+\Delta $时不为0，故 \(\delta_{\Delta}(t-k\Delta)\Delta\) 在$k\Delta \leqslant t \leqslant k\Delta + \Delta $时为1，其余为0。

\[\delta_{\Delta}(t-k\Delta)\Delta=\left\{\begin{array}{lc} 1, & k\Delta \leqslant t \leqslant (k+1)\Delta \\ 0, & \text { 其余 } t \end{array}\right. \]

那么有：

\[\hat{x}_k(t)=x(k\Delta)\delta_{\Delta}(t-k\Delta)\Delta=\left\{\begin{array}{lc} x(k\Delta), & k\Delta \leqslant t \leqslant (k+1)\Delta \\ 0, & \text { 其余 } t \end{array}\right. \]

\(\hat{x}(t)\)就是所有段的组合，用 \(x(t)\)和\(\delta_{\Delta}(t)\)表示\(\hat{x}(t)\):

\[\begin{aligned} \hat{x}(t)&=\sum_{k=-\infty}^{+\infty}\hat{x}_k(t) \\ &=\sum_{k=-\infty}^{+\infty}x(k\Delta)\delta_{\Delta}(t-k\Delta)\Delta \\ \end{aligned} \tag{1} \]

这里有一个关键点，就是 \(\delta_{\Delta}(t)\)的高度取值是 \(\frac{1}{\Delta}\)而不是1！。单就表示阶梯函数而言，脉冲函数的高度也是可以取1的，如定义脉冲函数\(\delta_1(t)\):

\[\delta_1(t)=\left\{\begin{array}{lc} 1, & 0 \leqslant t \leqslant \Delta \\ 0, & \text { 其余 } t \end{array}\right. \]

那么阶梯函数可以表示为：

\[\begin{aligned} \hat{x}(t)&=\sum_{k=-\infty}^{+\infty}x(k\Delta)\delta_1(t-k\Delta) \\ \end{aligned} \tag{2} \]

注意式（1）与（2）之间的区别在于式（1）的乘积项多一个因子 \(\Delta\)。
这两个式子都说明，阶梯函数可以表示为一串移位脉冲的加权和, 其中式（1）的加权因子为\(x(k\Delta)\Delta\)。
随着\(\Delta\)逐渐变小，\(\hat{x}(t)\)就逐渐趋近于\(x(t)\), 当\(\Delta\)趋向于0，则有：

\[x(t)=\lim_{\Delta \to 0}\hat{x}(t)=\lim_{\Delta \to 0}\sum_{k=-\infty}^{+\infty}x(k\Delta)\delta_{\Delta}(t-k\Delta)\Delta \tag{3} \]

这样，连续函数\(x(t)\)也可以理解为表示成了移位脉冲加权和的线性组合。
因为有：

\[\delta(t)=\lim_{\Delta \to 0}\delta_\Delta(t) \]

即宽度为\(\Delta\)高度为 \(\frac{1}{\Delta}\)的脉冲, 面积始终为1，在 \(\Delta\to0\) 时就变为单位冲激函数 \(\delta(t)\)，而式（3）实际上表示的是阶梯函数在 \(\Delta \to 0\)时的面积（如果不取极限，也就是阶梯函数的面积），根据面积与积分的关系，所以有:

\[x(t)=\int_{-\infty}^{\infty} x(\tau)\delta(t-\tau) \mathrm{d}\tau \tag{4} \]

这样，\(x(t)\)就表示成一个加权的移位冲激函数的和（即积分）。
式（4）为连续时间冲激函数的筛选性质。

卷积积分

一个线性时不变系统对单位冲激函数 \(\delta(t)\)的响应函数为 \(h(t)\), 那么，对移位的单位冲激函数 \(\delta(t-\tau)\)的响应就是 \(h(t-\tau)\)。
由于信号 \(x(t)\)可表示为一组单位移位冲激 \(\delta(t-\tau)\)的加权和，这里对冲激 \(\delta(t-\tau)\)的权是 \(x(\tau)\mathrm{d}\tau\), 因此 \(x(t)\)的响应\(y(t)\)可表示为一组移位冲激的响应 \(h(t-\tau)\)的加权和，其权也就是 \(x(\tau)\mathrm{d}\tau\)，因此，有：

\[y(t) = \int_{-\infty}^{\infty} x(\tau)h(t-\tau) \mathrm{d}\tau \tag{5} \]

式（5）称为卷积积分或叠加积分,记为信号 \(x(t)\)与信号 \(h(t)\)的卷积：

\[y(t)=x(t)*h(t) \]

与离散信号一样，卷积本质是\(y\)在时刻\(t\)的响应\(y(t)\)为信号 \(x(t)\) 的所有时刻信号的响应在时刻\(t\)的分量的叠加，也就是全部的\(x(t)\)对时刻 \(t\) 响应的贡献。

卷积的性质

卷积运算满足交换律、结合律和分配律：

交换律

\[x(t)*h(t)=h(t)*x(t) \]

分配律

\[x(t)*[h_1(t)+h_2(t)]=x(t)*h_1(t)+x(t)*h_2(t) \]

结合律

\[x(t)*[h_1(t)*h_2(t)]=[x(t)*h_1(t)]*h_2(t) \]