自变量变换
自变量变换
简单自变量变换的形式为 $ x(t)\implies x(at+b)$其中a,b是常实数. 这里包含了三种自变量变换：伸缩、反转和平移。变换的实质是在函数 \(x(t)\) 的基础上，对自变量进行变换，形成一个新函数，新函数为复合函数 \(x(t'), t'=at+b\)，这里函数符号使用相同的函数名 \(x\)， 意思是他们的值域是一样的，而且如果\(t'=t\)时，函数的值也一样。但是实际上，函数的自变量名称是可以随便换的，并不影响函数的实质，因此，实际上经过自变量变换的函数\(x(t')=x(at+b)\)和\((t)\)是t的两个不同的函数，它们的关系由变换式\(at+b\)的系数决定.
平移（时移）
变换式 \(at+b\) 中 \(a=1\) 时,变换式变为 \(t+b\), 变换后的函数记为 \(x(t+b), b \in \mathbf{R}\),这种变换叫平移，如果自变量为时间\(t\)，也称时移。
左移（超前）
对于函数 \(x(t)\)进行自变量平移变换后的函数 \(x(t+b), b\in \mathbf{R}, b>0\), 实质上是当 \(x(t)\) 取 \(t=t_0\) 时 \(x(t_0)\) 的值对应于 \(x(t+b)\) 而言为 \(t+b=t_0\) 时 \(t=t_0-b\)的值,也就是 \(x(t+b)\) 的自变量\(t\)要比\(x(t)\)的\(t\)小一个\(b\)值，相当于\(t\)向坐标轴左移\(b\)的大小，从曲线的图上看就是图左移了\(b\)的大小。由此可见，对 \(x(t)\) 进行自变量的平移变换一个正数形如 \(x(t+b), b>0\)为左移或超前平移。
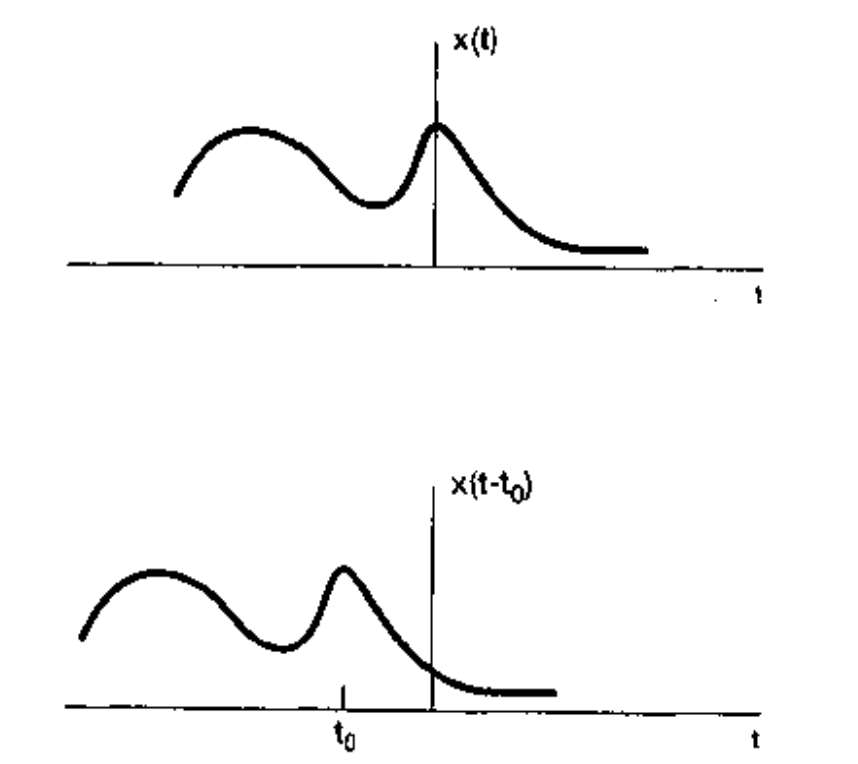
右移（滞后）
如果\(b<0\),可改写为\(x(t-b)，b\in \mathbf{R}, b>0\),则移动方向与\(x(t+b)，b\in \mathbf{R}, b>0\)相反，为曲线右移 \(b\) 的大小。对于时间为自变量的信号而言，左移称为超前，右移称为滞后。 由此可见，对 \(x(t)\) 进行自变量的平移变换一个负数形如 \(x(t-b), b>0\)为右移或滞后平移。
反转
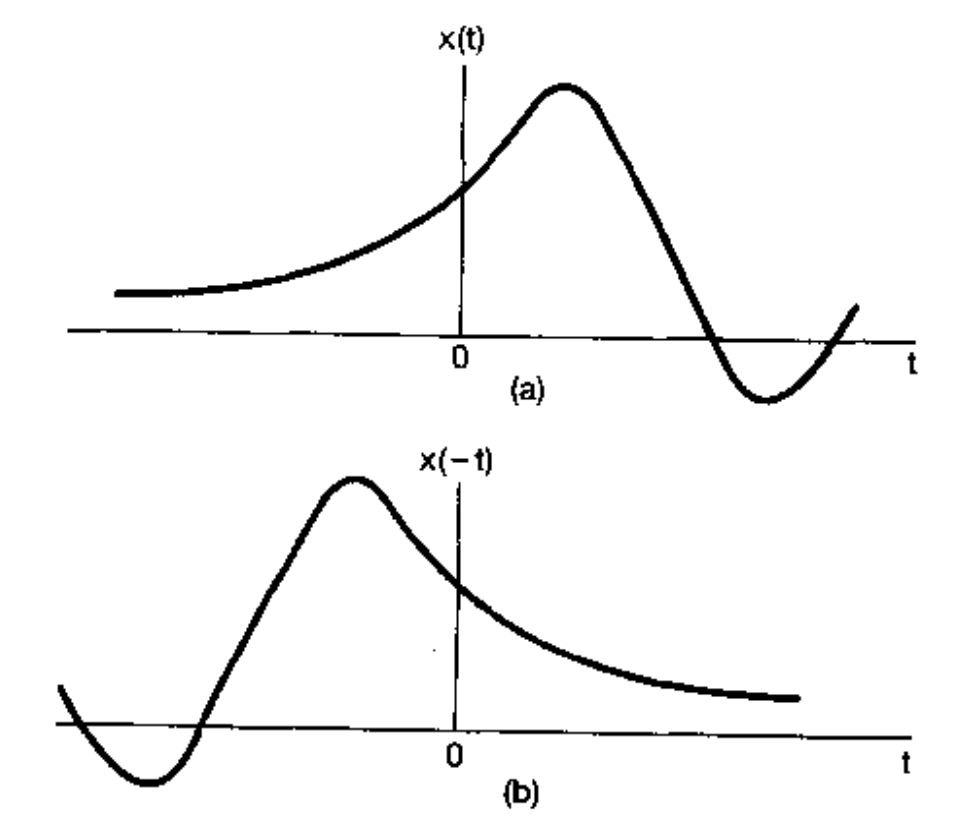
变换式 \(at+b\) 中 \(a=-1, b=0\) 时,变换式变为 \(-t\), 变换后的函数记为 \(x(-t)\),这种变换叫反转。反转的实质是 \(x(t)\)取 \(t_0\)时的值对应于\(x(-t)\)的自变量 \(t=-t_0\) 的函数值，也就是说变换前和变换后的函数当自变量为原点的对称点时函数值相同，图形上就是它们为因变量坐标轴的对称图形，\(x(t)\)的图形被\(x(-t)\) 沿因变量的轴反转了。
伸缩（尺度变换）
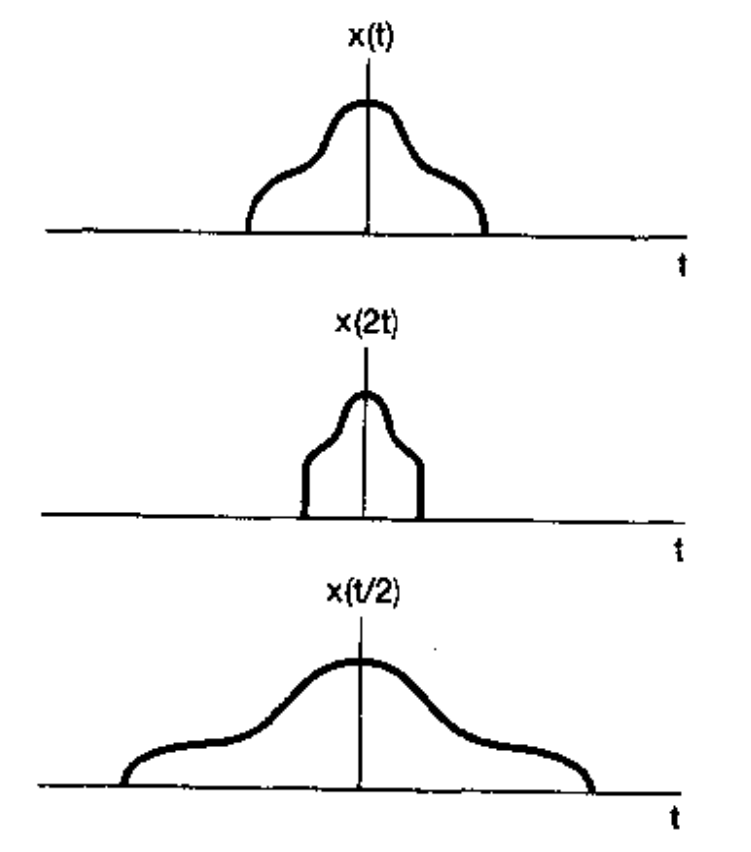
变换式 \(at+b\) 中 \(b=0\) 时,变换式变为 \(at\), 变换后的函数记为 \(x(at)\)，当\(a>0\)时，这种变换叫伸缩变换或尺度变换。伸缩变换的实质时当 \(x(t)\) 取 \(t=t_0\) 时的值对应于 \(x(at)\) 取\(t=\frac{t_0}{a}\)时的值，即相对于 \(x(t)\)的自变量，\(x(at)\) 的自变量在两个函数对应相同值时，\(x(at)\)的自变量被压缩了 \(a\)倍，对应的图形就是基于因变量轴为对称轴压缩了\(a\)倍，如果\(a>1\)， 图形被缩小到\(\frac{1}{a}\)，反之，\(a<1\) 时，图形被放大到 \(\frac{1}{a}\)倍。或者换种写法，设 \(a>1\), 那么\(x(at)\)是将\(x(t)\)的图形缩小\(a\)倍，\(x(\frac{t}{a})\)是将\(x(t)\)的图形放大\(a\)倍。注意，他们都是基于\(t=0\)的轴线伸缩的。
组合变换
变换式 \(at+b\) 可改写为 \(a(t+\frac{b}{a}),a\ne0\), \(x(t)\) 当 \(t=t_0\)时的值对应\(x(at+b)\)相同值的\(t\)如下式所得：
由上式可见，按步骤先伸缩和反转，再平移即得。\(at+b\)，先伸缩和反转后再平移，平移的量要缩放 \(\frac{1}{|a|}\)倍，而平移的方向与\(a\)的符号也相关，即与是否反转是相关的。
反转和伸缩的先后顺序无关紧要，哪个先变换，其结果是一样的。
如变换式 \(at+b，a<0\) 可改写为 \(-a(t-\frac{b}{a}),a>0\), 这时缩放反转后，平移的方向就要反向。
变换也可先平移再伸缩反转，结果是一样的。
参考https://www.kxting.com/article/20221019/355864.html
两种方法：可变对称抽和固定对称抽。
1、可变对称抽：
在三种基本变换中， 反转是相对于对称轴 \(t = 0\) 进行的， 而尺度变换中无论\(a\)为何值，\(t = 0\) 的信号 \(x(0)\) 也是不变的。然而对于时移变换，相当于所有的时间变量所对应的信号值发生了一个依时间的位移，这时原来 \(t = 0\) 对应的信号 \(x(0)\) 发生了一个位移。这时可以以原来 \(t = 0\) 为轴，考虑信号的变换。该方法的关键点如下：
a. 找到伸缩、反转的对称轴，经过自变量为零的\(t\)值点作垂线，该垂线为对称轴。
b. 存在时移变换时，对于\(x(-at-b)=x(-a(t+\frac{b}{a}))\)，则应将自变量换成 \(t'=t+\frac{b}{a}\) 。也即变成\(x(-at-b)=x(-at')\) 。 由于变换过程都是只针对时间自变量\(t\)本身， 因此对称轴为使得 \(t'=0\) 的\(t\)，也即 \(t=-\frac{b}{a}\)。
2、固定对称抽：
该方法对于时移变换并不考虑作时间变量\(t\)的代换，也因此其对称轴不发生任何的改变。平移时需要提取 \(t\) 前面的系数，反转和伸缩变换时直接以 \(t = 0\) 轴进行变换。两种方法的本质是一致的，不同在于对待时移变换时，参考的变量不同。
