论文笔记二：《A Tutoral on Spectral Clustering》

首先谱聚类是非常流行的一种聚类，比一般的k_means效果要好，不仅如此，谱聚类里包含很多很有用的知识值得学习，比如拉普拉斯图和一些很好的思想，下面简单记录一下对于这篇论文的笔记。

对于这篇论文基础的一些讲解，包括相似图的定义，度矩阵的定义，还有不同类型的相似图等都在这篇博客里有很好的体现，所以在这里就仅仅写一些自己的理解。

https://www.cnblogs.com/pinard/p/6221564.html

一、想特别记录一下拉普拉斯图的一些性质，因为感觉虽然这个算法可能已经过时了，但是Laplacian graph现在仍然有很多应用场景。

拉普拉斯图是度矩阵和权重矩阵的相减得来的，所以他有一下这几种性质。：

1、他是实对称阵。这一点很重要，意味着他可以做特征分解。

2、他满足： 

 

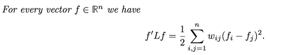
这一点满足了他是半正定的，而且最小特征值等于0，很好证明，把特征等式式子变换一下就得到。

3、既然是半正定的那么一定有所有n个特征值大于0.

4、他的重复最小特征向量的（也就是0）个数等于图的连通分量的个数。并且对应的特征向量为指示向量（证明分为一个连通分量和多个连通分量来证明，其中主要思想是把多个连通分量的情况转化成了由多个单连通分量图的分块对角阵）

5、Laplacians图分为标准化和非标准化的图，其中在实际应用中三者都可以用，但是在论文8.5中说明了一般标准化的图要比非标准化的图要好一些，而且那里给出了一些条件。

二、之后说了两种图割算法 RatioCut和Ncut这部分有如下部分想要记录：

1、首先说图割的思想，就是一种图算法的分割，使分割间的权重和最小，割内的权重和最大。将这个任务形式化的表述可以得到： 

 

如果直接最小化这个式子做优化当然也是可以的，但是会出现很糟糕的效果， 

 

 

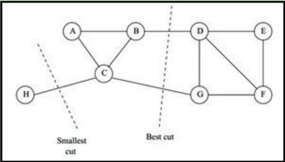
比如上图，他只考虑了图权重的大小关系，没有考虑到分割点数量或者度的关系，由此思想延伸除了两种著名的图割：

 

 

 

 

 

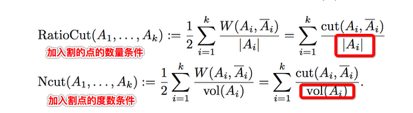
2、在证明两种图割的时候思想差不多都是定义了f向量的形式，之后转化成一个带约束的最小化问题，再根据一个神奇的理论证明出这个解的结果就是图的k个最小特征值对应的特征向量对应的指示函数。（其中有一些数学地方没太懂，比如：不过先忽略吧。。） 

 

 

 

 

 

三、之后论文介绍除了图割方法还介绍了两种证明方式，包括随机过程和微扰动理论，这两个部分没仔细看，先mark一下，以后要是用到了再回来仔细研究。

四、第四部分说了如何使用谱聚类，包括参数选择，图的选择，簇个数的选择、相似性矩阵的选择等等，但大部分是一些经验性的内容，并没有严格的推到，我这部分大致看了一遍，同样以后用到了再回来仔细研究。

五、最后想说说对这个算法的理解：

先上算法本身： 

 

这是Ncut版本的，其他版本的都差不多，就是用不同的拉普拉斯图的问题。

我感觉这个算法的实质就也是一种降维，我们用PCA做比较。

PCA想要的是找到高维度在低纬度投影保持数据方差尽可能大并且线性无关的一组基并且映射过去，那么这个映射的版本就大限度保持了数据在原始空间的性质。

而对于Spectral Clustering来说首先明确一点：

图割是一种降维

相当于理解成每一个子图都是抛弃掉了其他子图后得到的降维后的结果，只不过保留条件从PCA的『直接减掉（感觉相当于割掉一些离中心远的点）』变成了『割掉类间相似度小的点，使得类内的点尽可能相似』，从这个角度来说对拉普拉斯矩阵的特征分解可以看成是降维的另一种形式，只不过降维的条件变了。

而从图的重构角度来看，拉普拉斯矩阵分解后的特征向量能够尽可能恢复原来的graph信息。