最大子段和的DP算法设计及其效率测试

表情包形象取自番剧《猫咪日常》
那我也整一个
曾几何时,笔者是个对算法这个概念漠不关心的人,由衷地感觉它就是一种和奥数一样华而不实的存在,即便不使用任何算法的思想我一样能写出能跑的程序
直到一年前帮同学做了个手机游戏demo才发现了一个严峻的问题
为啥*一样的画面能跑出ppt的质感?
虽然发现当时的问题主要出现在使用了一个有bug的API,它导致了低性能的循环调用,但是从那时便开始就重新审视算法了,仅仅一个函数就能大幅地改变程序带给用户的体验这个观念根植心底
后来多多少少也学习了一些算法的知识,这回一看到这次要解决的问题有点来头,叫 最大子段和 ,多亏笔者知识面狭隘,未曾了解过前人的解决方案,于是就萌生了“整一个算法解决吧”的想法,可设计的算法直到写这篇blog为止,结果还不甚理想,可后来笔者发现了原因居然是MStest中一个微妙的缺陷,这种经验值得分享,就想着把这次的设计经过也写进来吧,于是便催生了本文
本文原意在于分享一次算法设计的经历,如果有概念上的错误和纰漏劳请各位指正,笔者在叙述中会尽可能的避免涉及到算法的一些名词概念,尽量保证所有读者都能无障碍的阅读,篇幅较长,但是希望读者能从中得到一些感悟,本文最终实现了一种比较优雅的算法,时间复杂度近似O(N)
整个项目的代码都在 腾讯云 中,根据需要可以自行下载,注意:笔者使用语言为C#
那没得说了,开干

有想法就要去做,首先,我们得分析最大子段和这个问题的域
子段数组
这样是不是就好理解了?最大子段问题如果不进行推广,狭义地定义在数组中就是本文要解决的问题了,或者应该说这次的问题就是如何得到最大子数组和
连续
这其实是隐含的条件,实际上没必要单拎出来说,只是为了确保思路的连续性,而在得知了这两项要求的情况下,我们很容易找到这个问题的第一个解决方案:
- 找到当前数组的所有子数组
- 找出其中数组和最大的
这就是最容易理解的穷举的方法,在后来上网查阅相关代码时,该算法的实现也是被列在第一个,可既然要设计算法,就自然要尽量寻找它的更优解,算法出现的本意也是找到更高效的方式解决同一问题,可即便如此,理解这种方法也对我们接下来理解笔者蹩脚的设计大有帮助,因为看到最后大家会察觉到这种算法设计的思路其实是一种更高效的穷举,或者说是一种穷举搜索模式
两个简单的设计
我们理解了要找出数组和最大的子数组是问题的最终解,而解域则是原本数组的幂集,也就是需要穷举的解数量多达2^n,这显然不是我们乐于见到的问题规模,由此,笔者断定解决问题的关键在压缩原问题的“尺寸”
压缩
对于这个问题,我们要看到它的本质,无论什么样的子数组都是由连续的原数组内元素组成的,而元素可以分成三类:
- 正数
- 负数
- 0
这三类元素对子数组的影响也能分成三类:
- 增大
- 减小
- 不变
而分散在数组里的各种元素的分布只有两种状态:
- 连续
- 穿插
连续的任一元素造成的影响都不会改变,比如连续的正数依旧会增大子数组,于是笔者就写出了该算法的第一个函数Compress()
public ArrayList Compress(ArrayList arr)
{
int previousSum = 0;
if (arr.Count >= 2) //在获取值之前判断该容器是否需要判定
{
previousSum = (int)arr[0];
}
for(int i=1;i<arr.Count;i++) //合法数组长度大于等于2
{
if(previousSum>=0)
{
if((int)arr[i]>=0)
{
previousSum += (int)arr[i];
arr.RemoveAt(i);
i--;
arr[i] = previousSum;
}
else
{
previousSum = (int)arr[i];
}
}
else
{
if ((int)arr[i] < 0)
{
previousSum += (int)arr[i];
arr.RemoveAt(i);
i--;
arr[i] = previousSum;
}
else
{
previousSum = (int)arr[i];
}
}
}
return arr;
}
虽然用到了C#中的ArrayList(),但是它在C++11标准后有Array这种类似实现方式,在别的语言中相当于一个容器类的实现
这个函数的功能是整合目前数组里连续的正数和负数,具体的逻辑操作是根据判断当前的连续和与下一个元素的符号是否相同
找到那个最大的家伙

接下来看看这个被我们压缩打包的数组,里面(应该)整整齐齐地排好了我们想要的元素,有正有负,相互交叉,很好,准备工作做完了,我们接下来要用简单的方式处理这个整齐的元素队伍
算法设计的重点:
我们无法确定现在究竟有多少个元素在我们的手里,但我们可以处理至少有一个元素的情况,我们的算法最后也会处理至少一个元素以上的情况
而当我们手里只有一个元素时,我们只需要判断它是否是负数,如果不是负数,那么最大子数组的值就一定是它了,那么当我们手里有两个元素的时候呢?我们按照顺序的方法处理:
如果第二个元素是负数,我们绝对不会考虑把它和第一个元素加和
这个原则就是该算法设计的核心思路,思维敏捷的读者应该能从这些叙述中感觉到一些眉目了,我们就继续往下处理三个元素的情况
三个元素或许只是增加了一个元素,但不免让人想的更加复杂长远,比如考虑这些元素的值的正负,是否会出现特殊情况等,但是我们先不去这么想,因为我们虽然不太清楚三个元素的处理方式,但我们已经很了解两个元素要如何处理了,那么先处理后两个元素,这个操作我们刚刚做过
如果第二个元素是负数,我们绝对不会考虑把它和第一个元素加和
眼熟吧?这里可以再补充一下这个逻辑:
如果第二个元素是正数,我们一定要把它和第一个元素加和
“这也太简单了吧?”
没错!就是这么简单,分析到这一步我们要解决的问题的本质已经清晰可见了,当我们把这后面的两个元素处理完就会得到它们组成的“数组”的“最大子数组和”,此时我们需要把这个值储存下来,那么这个存下来的值要作为以后出现的新的“最大子数组和”的参考,如果新值大于它,则要进行更新,而我们的元素也会因此进行整合,它们的“最大子数组和”的值就会变成新的元素
这里笔者用双引号括上了最大子数组和的原因是因为它其实并不是一个严格意义上的最大子数组和,我们接下来继续解释
第二个重点:
注意前文中所说的方法,全都在优先处理第二个元素,没错,这就是本算法的另一个核心要点,我们不论第一个元素的正负,这使得最终到达算法边界时,会得到一个使第一个元素尽可能的大的连续数组和
重新递推我们上文的公式,我们会发现每次得到的“最大子数组和”都是有可能为负值的,因为它实际上并不是最大子数组和,而是为当前元素提供一个更大的可能的取值,使得当前处理的元素尽可能的变为更大的值,而就是经过这样一轮处理,在递归结束时我们的整个数组每一个元素都会获得自己尽可能大的连续数组和的结果,到最后,这其中最大的并且大于0的那个就是我们要求的最大子数组和
其实不难发现,我们的算法最终实现也是基于一种穷举的思想,我们将当前状态的最优值穷举出来,并每次都与当前存储的最大和进行判断,但比起前文提到的穷举法,我们将穷举每一种数组和变成了穷举每一个元素的最大连续数组和,这就是最终提高了效率的原因,也是 动态规划法 被普遍视作穷举算法的优化形式的原因
动态规划(Dynamic Programming,DP),这里是行文至此第一个对初学算法或者不太了解算法的读者而言比较陌生的词汇,但是多少都有听说过,它有个近亲叫分治(Divide and Conquer,D&C),而两者的区别用三言两语很难说清,给感兴趣的读者的建议是去看对应问题的实现代码和编写者的解释,很容易找到区分二者的感觉
这里给出第二个函数SearchForLargest()的代码,代码有一些细节的优化,但大体上的思路是一致的
public int SearchForLargest(ref ArrayList arr,int start)
{
if (start < arr.Count)
{
largestSum = Math.Max((int)arr[start], (int)arr[start] + SearchForLargest(ref arr, start + 1));
}
if (largest < largestSum)
{
largest = largestSum;
}
return largestSum;
}
public int largestSum = 0;
public int largest=0;
其实还有一点,笔者就算不提,很多人也看出来了,没错,该算法的代码依旧有优化的空间,比如第一个函数Compress()完全可以不要,可笔者觉得算法本身要联系到应用,Compress()函数可以作为在初始化阶段压缩数组的手段,在需要时进行最大子段和的计算,因此没有删除Compress()函数以及有关它的叙述
那是真的牛啤这也太酷了吧

“这难道就是最大子段和的最优算法了吗?”
你好,不是的,这里给出比较酷的,O(N)级别算法的代码
static public int EasyGetLargestSub(ArrayList arr)
{
int largest = 0;
int largestThisSub = 0;
foreach(int i in arr)
{
largestThisSub = Math.Max(largestThisSub + i, 0);
largest = Math.Max(largestThisSub, largest);
}
return largest;
}
是不是看到如此简单的代码实现感觉自己像是被泼了一盆冷水?刚刚看了笔者一顿分析猛如虎到头来更优化的算法仅仅是一个单循环?
当然了,刚刚上文提到过笔者设计的DP方案也可以精简到类似的厚度,虽然时间复杂度可能不如这种算法低,可本文的主要意义也不在于比较算法的优劣,而是为了分享设计的思路,笔者的初衷是让任何一个用心看完本文的人都能在面对类似简单的DP算法时能露出会心一笑,进而能够开始理性地分析算法的用意
虽然理论上讲,任谁花几个小时去设计算法最后发现还不如一个单循环心态都不会很好,可笔者亲眼看到这种实现的时候却前所未有的释然,因为确实学习到了它抽象的理念,也多亏如此才会继续完善自己的算法,才会有本文的出现,这种体验也是笔者想传达出去的,希望大家可以去尝试设计算法并能有所收获
顺带一提,这种算法师出有名,叫Kadane算法,运用的是数学归纳的思想,笔者仅仅是用微不足道的思考和应用一些设计理念去做该算法的设计的,数学应用一直是笔者的弱项,毕竟笔者的一项知名记录是高数(上)连挂三年
相关算法的一些后话
这里再简单地讲一下动态规划(DP)和分治法(D&C)两者的异同,可以选择性阅读
两者的共同点都在用把大问题划分为小问题的思想解决复杂的难题,众所周知,量变会引起质变,解域的扩张也是这样,所以只要收缩问题的规模,解决问题的效率就会几何级的提升,这就是两者优化穷举的核心理念
网上有总结二者的区别是动态规划法在各个子问题间存在联系,而分治法是子问题相互独立,其实这要看对联系的定义了,笔者觉得不甚明了,所以这里给出两个例子:
快速排序 —— DP
0-1背包问题 —— D&C
这两个例子是笔者在读《算法图解》的时候书中介绍的典型例子,这本书是很优秀的入门书,学有余力的朋友更建议配合算法实例进行阅读,同时也能巩固对算法的理解。
使用MStest进行单元测试
好的,那么刚刚的算法设计的篇章告一段落了,整理一下心情,我们开始进入另一个环节,利用MStest进行单元测试,上一篇blog中有提到如何使用MStest,想要了解的读者可以点击这里
那么题外话到此为止,这里测试的代码我们直接选择了上文提到过的O(N)级别(Kadane)算法的代码,因为不得不承认,它的代码逻辑很好整理...
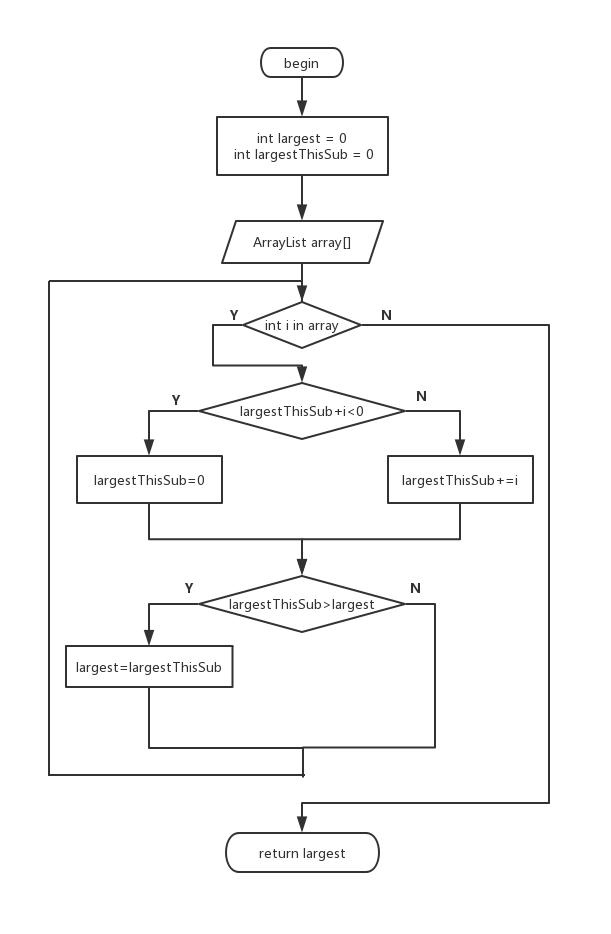
tadang~笔者应该不用解释为什么这里会有一张流程图吧,既然要进行白盒测试几乎必需一个程序流程图,好让我们直观的明白在各种情况下程序会到达一个什么样的状态,但我们仍需要手工记录自己用例能覆盖的条件和路径,这里强力推荐黑科技——PS,可以用不同的图层表示这是第几个用例,或是用例中的第几个状态,使用得当你会得到类似下面的效果
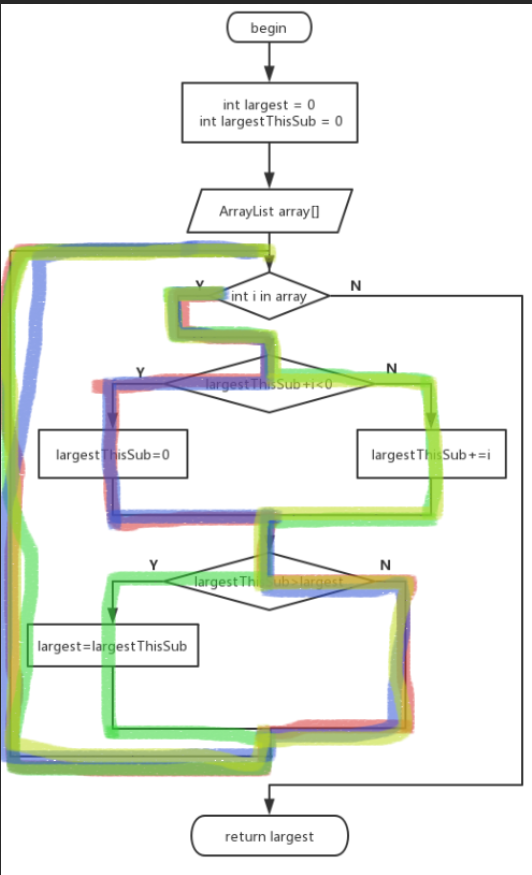
这里的初值选择了1,然后逐渐改变数组的值,到达上图状态是覆盖的极限,那么由此分析可知该段代码有不可达的一条路径,原本两个串连条件判断可以得到四个路径,因此只剩下了三种不同路径,如图所示其实一个用例就可以完成这个测试了,但是还有一条退出路径,我们也尽可能地向路径覆盖的级别去做这个简单的测试,那么就要编写三个测试用例使得每一个路径最终都能接上一次该退出路径
测试用例最后的选择需要我们将刚才选择的条件值整形化,最后得出三个测试用例分别为:
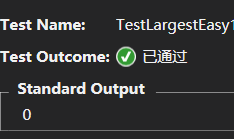
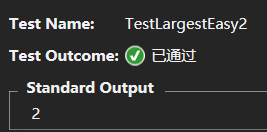
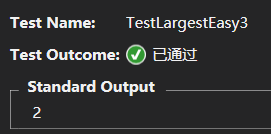
告一段落?
怎么可能这么轻易地放过测试自己算法的一次机会?自己的孩子再孬也得让他试试!
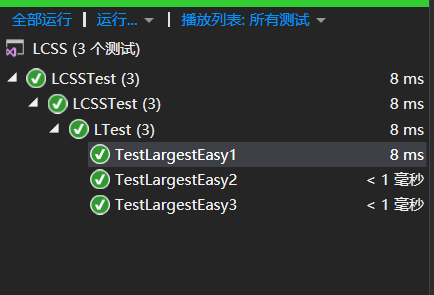
测试样例,全部运行!
这里引入了一些白盒测试的用例,但是默认输入合法(输入一个合法的数组),因此引入的用例均为边界测试,主要是防止自己的程序出现无法处理的合法内容,其中包括:
- 全正值输入 TestAllPositiveArrayInput()
- 全负值输入 TestAllNegativeArrayInput()
- 全0输入 TestAllZeroArrayInput()
- 空数组输入 TestEmptyArrayInput()
接下来就是主角们...
- 测试压缩寻找最大子段的算法(本文dp算法) TestCompressAndLargest()
- 测试Kadane算法 TestLargestEasy()
测试用例不出所料的都通过了,可...

???

这执行效率的差距也太过分了!!!
究其原因,这原来是个...
大扑棱蛾子

笔者这里分析过函数本身的问题,比如传值使用引用传递,或者压缩函数有缺陷,或是用例选择特殊,同时使用Stopwatch(C#的运行时间计时器)来进行监控,但都不是,最终得到的结论是:
这是目前MStest的一个bug
它的第一个测试用例永远会是一个超长的时间,最差的一次甚至达到了40ms,只要将你一个后面的测试用例复制粘贴到第一个用例的前面就可以得到正常的结果了,最好粘贴两个以上才能保证后续用例基本正确,这是后来进一步测试的结果
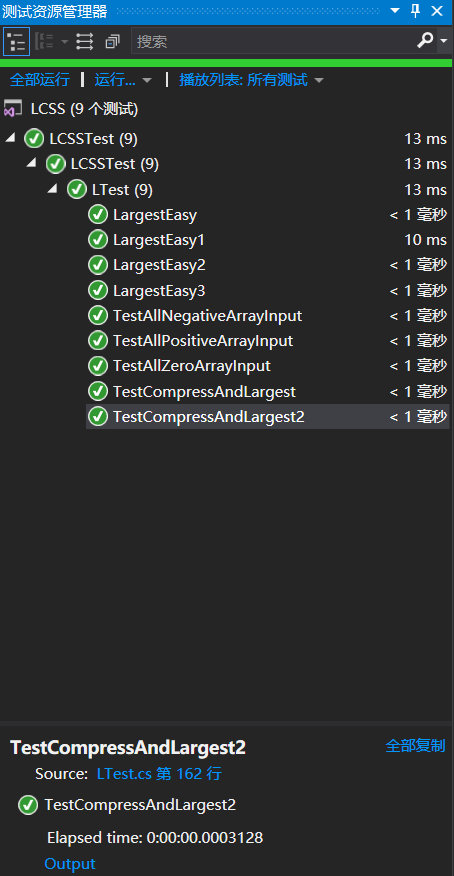
笔者不太了解其它的测试框架,所以不敢随意猜测是否是框架的特点,目前只能认为它在测试框架启动时第一个用例的运行时间计时器就开始计时了,而第一个用例此时还没有运行,从而产生了错误计时
最后在测试用例中本算法最终仍比Kadane算法慢大约logN倍的时间,根据网上的一些资料从而得出本算法属于O(NlogN)级别算法的结论(但是这递归看着挺好看的)
总的来说
笔者这次收获很多,在写blog的过程中也在不停地理顺着思路,优化着代码,这是一个很劳费心神却又很快乐的过程,希望各位同样劳神读到现在的朋友一样有所收获,感谢您的阅读。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号