n阶贝塞尔曲线

新博客：https://yinl.fun
欢迎关注，同步更新

贝塞尔曲线

本文章借鉴自Unity中的曲线绘制.

贝塞尔曲线(Bézier curve)是由法国数学家Pierre Bézier所提出,类似于Photoshop软件中的钢笔工具,不过钢笔工具仅仅只是用了二阶贝塞尔曲线.

原理

在我们写代码之前还是了解一下原理为好,所以贝塞尔曲线的原理就是利用经过所有直线上的点的差值来进行绘制,如图为二阶曲线

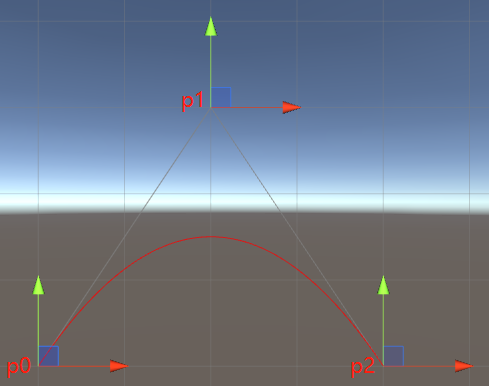
下面给出二阶曲线的公式,P0,P1,P2为示例图上三点,t为差值数据:

$$ B(t) = (1 - t)^2P_0 + 2t(1 - t)P_1 + t^2P_2 , t\epsilon[0,1] $$

而一阶曲线自然就是一个直线,公式为:

$$ B(t) = P_0 + (P_1 - P_0)t = (1 - t)P_0 + tP_1 , t\epsilon[0,1]$$

从中我们可以发现规律从而推导到n阶的公式:

$$ B(t) = \sum_{i=0}^nPi(1 -t)^{n-i}t^i , t\epsilon[0,1]$$

而我们要在Scene窗口绘制出贝塞尔曲线,所以这里用到Editor类下的OnInspectorGUI函数绘制Inspector窗口中的贝塞尔曲线配置,OnSceneGUI函数中绘制真正的贝塞尔曲线,绘制方式我们利用Handles函数进行直线模拟曲线方式的绘制.

代码

首先我们需要一个数据类Curve,存储简单的Vector3数组

// 贝塞尔曲线数据
public Vector3[] points;

然后我们需要一个Editor类这里我们起名为CurveTool,继承自Editor并重写刚才说的两个函数,此处代码不懂可以看我之前写过的文章: Unity编辑器

public override void OnInspectorGUI()
{
    serializedObject.Update();
    EditorGUILayout.BeginVertical();
    EditorGUILayout.PropertyField(points, new GUIContent("坐标组"), true);
    EditorGUILayout.EndVertical();
    serializedObject.ApplyModifiedProperties();
}

然后接下来时重写OnSceneGUI函数了,不过在之前我们要看看具体怎么用代码来实现刚才的N阶曲线.
因为我们要利用直线来绘制,所以需要一个for循环来执行绘制,利用GetPoint函数来获取具体每个精度点的位置然后绘制直线就好了.

Vector3 lineStart = GetPoint(0f); // GetPoint函数为获取当前点的位置
for (int i = 1; i <= curve.lineSteps; i++) // lineSteps为绘制精度
{
    Vector3 lineEnd = GetPoint(i / (float)curve.lineSteps);
    Handles.DrawLine(lineStart, lineEnd);
    lineStart = lineEnd;
}

每次取差值就能减少一阶,所以利用递归从n阶到最后的一阶然后的返回值就是最终点的位置.

public Vector3 GetPoint(float t)
{
    Vector3[] pos = new Vector3[curve.points.Length];
    pos = (Vector3[])curve.points.Clone();
    return curve.transform.TransformPoint(GetLerpPoint(pos, t));
}

public Vector3 GetLerpPoint(Vector3[] pos, float t)
{
    if (pos.Length == 2)
    {
        return Vector3.Lerp(pos[0], pos[1], t);
    }
    Vector3[] newPos = new Vector3[pos.Length - 1];
    for (int i = 0; i < pos.Length - 1; i++)
    {
        newPos[i] = Vector3.Lerp(pos[i], pos[i + 1], t);
    }

    return GetLerpPoint(newPos, t);
}