判断点在多边形内部
点在多边形内部的判断有很多种方法,性能最好也准确的算法应属射线法。
射线法思想
射线法是由从点出发向一个方向发送射线,判断与边相交的次数,如果为奇数则为多边形的内部,如果为偶数则为外部。
首先是数据类,存储多边形的点和最大最小的XY,用来做快速判断
// 多边形点的数据存储
class PolygonConfig
{
public float maxX;
public float maxY;
public float minX;
public float minY;
public List<Vector2> points = new List<Vector2>();
public void SetMaxAndMinXY()
{
if (points.Count > 0)
{
maxX = points[0].x;
maxY = points[0].y;
minX = points[0].x;
minY = points[0].y;
}
for (int i = 1; i < points.Count; i++)
{
maxX = Mathf.Max(maxX, points[i].x);
maxY = Mathf.Max(maxY, points[i].y);
}
}
}
下面是判断的核心方法
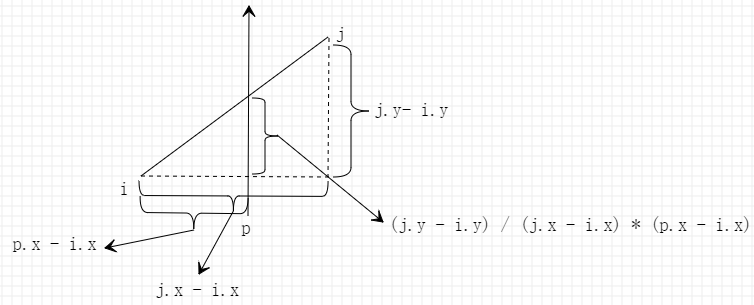
- 首先是通过最大最小的XY来快速筛选点是否在四边形中
- 核心代码部分
- 这里我们做向上的射线(射线方向随意,这里我们向上做)
- 第一组判断(points[i].x <= point.x && points[j].x > point.x) || (points[j].x <= point.x && points[i].x > point.x) 这里主要的意思就是点的x坐标是否在多边形的一个边的x轴坐标内。(可理解成: i.x < p.x < j.x)
- 第二组判断(points[j].y - points[i].y) / (points[j].x - points[i].x) * (point.x - points[i].x) + points[i].y > point.y 让我们分开来理解,首先是(points[j].y - points[i].y) / (points[j].x - points[i].x)是x轴差值和y轴差值的比值,(point.x - points[i].x)是点与边中一点的x轴差值,两者的相乘就确定了一个y,y值再加上那边中一点的y值,如果大于点的y则穿过,否则没穿过。
- 进过所有边的判断完成后,奇数为在中心,所以小技巧就是inPolygon的取反。
private bool IsPointInPolygon(PolygonConfig polygon, Vector2 point)
{
// 构建矩形,进行快速筛选
if (point.x > polygon.maxX || point.x < polygon.minX || point.y > polygon.maxY || point.y < polygon.minY)
{
return false;
}
bool inPolygon = false;
var points = polygon.points;
for (int i = 0, j = points.Count - 1; i < points.Count; j = i++)
{
if (((points[i].x <= point.x && points[j].x > point.x) || (points[j].x <= point.x && points[i].x > point.x))
&& ((points[j].y - points[i].y) / (points[j].x - points[i].x) * (point.x - points[i].x) + points[i].y > point.y))
{
inPolygon = !inPolygon;
}
}
return inPolygon;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号