证明正弦定理的多种方法

证明正弦定理的方法

方法汇总

第一种 最简单的方法

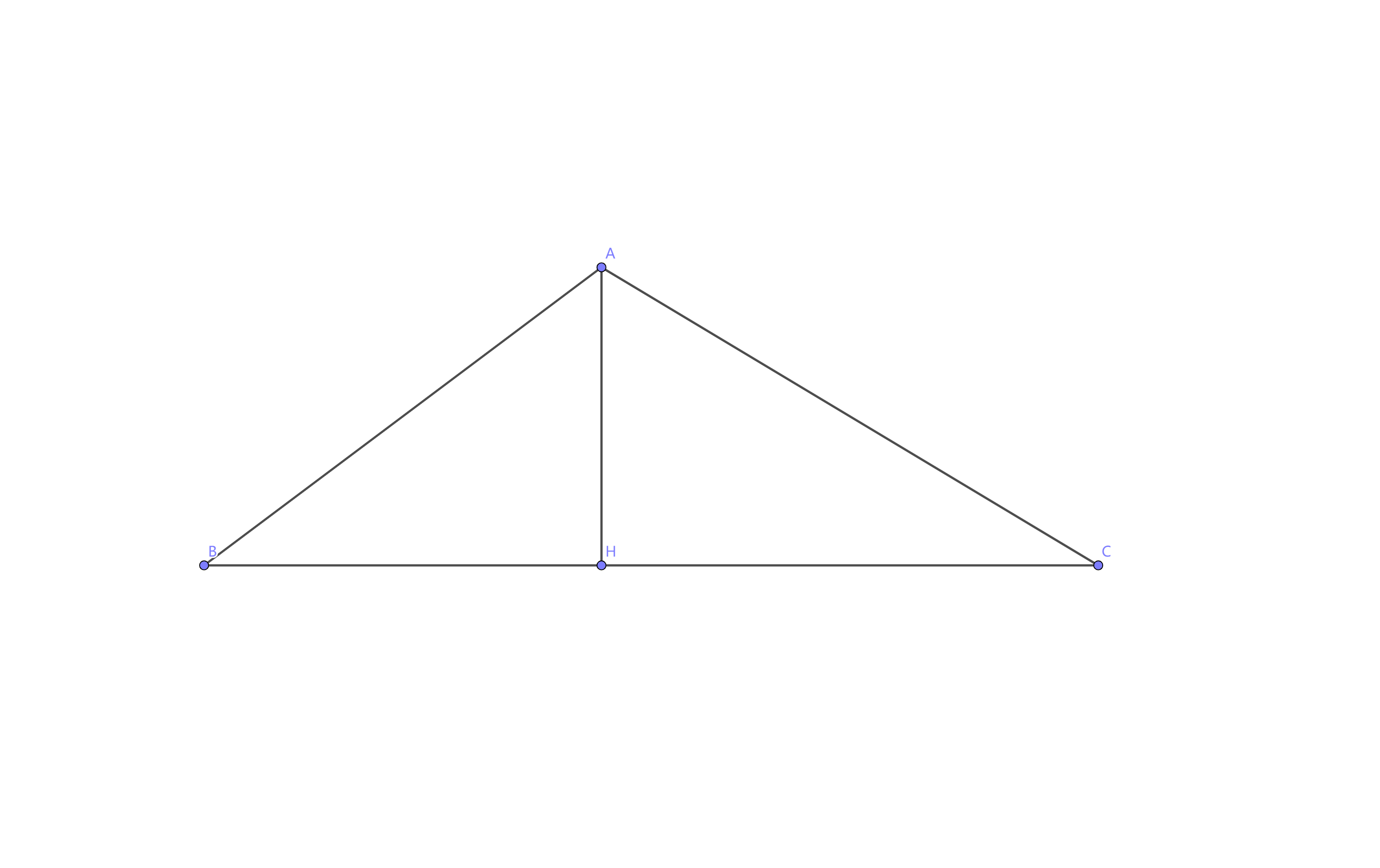
过点 $A$ 作 $AH\perp BC$ 交 $BC$ 于点 $H$ ， 易得：

$$\begin{gathered} AH=c\sin B=b\sin C \\ \Downarrow \\ {\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{b}{\sin B}} \end{gathered}$$

同理可得：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}$$

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{a}{\sin A}}$$

综上：

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{a}{\sin A}}$$

补充：

我们也可以借此得到 $S\mathrm{△}ABC={\displaystyle \frac{1}{2}}ab\sin C={\displaystyle \frac{1}{2}}ac\sin B={\displaystyle \frac{1}{2}}bc\sin A$

第二种 勾股定理法

过点 $A$ 作 $AH\perp BC$ 交 $BC$ 于点 $H$ ，可得 $AH=b\sin C,BH=c\cos B$

由勾股定理可得：

$$A{B}^2+A{H}^2+B{H}^2$$

即

$$\begin{gathered} c^2=b^2{\sin }^{2}C+c^2{\cos }^{2}B \\ \Downarrow \\ {c}^2(1-{\cos }^{2}B)=b^2{\sin }^{2}C \\ \Downarrow \\ {\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{b}{\sin B}} \end{gathered}$$

同理可得：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}$$

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{a}{\sin A}}$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

第三种 余弦定理证明正弦定理

前言：暴力出奇迹 打表出省一

$$\cos A={\displaystyle \frac{c^2+b^2-a^2}{2bc}}\Rightarrow {\cos }^{2}A={\displaystyle \frac{c^4+b^4+a^4+2c^2{b}^2-2a^2{b}^2-2a^2{c}^2}{4b^2{c}^2}}$$

由 ${\cos }^{2}A+{\sin }^{2}A=1$ 可得：

$${\sin }^{2}A={\displaystyle \frac{-c^4-b^4-a^4+2c^2{b}^2+2a^2{b}^2+2a^2{c}^2}{4b^2{c}^2}}$$

同理可得 ${\sin }^{2}B$ 和 ${\sin }^{2}C$ 的值，笔者不在此赘述此证明过程。

所以：

$$({\displaystyle \frac{a}{\sin A}}{)}^2={\displaystyle \frac{4a^2{b}^2{c}^2}{-b^2-c^2-a^2+2a^2{b}^2+2a^2{c}^2{b}^2{c}^2}}=({\displaystyle \frac{b}{\sin B}}{)}^2=({\displaystyle \frac{c}{\sin C}}{)}^2$$

所以：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

第四种 建立平面直角坐标系

不妨设 $A(0,0),C(x,y),B(c,0)$ ，过点 $C$ 作 $CH\perp AB$ 交 $AB$ 于点 $H$ ，易得：

$$\begin{gathered} C{H}^2=y^2 \\ A{C}^2=x^2+y^2 \\ B{C}^2=(x-c{)}^2+y^2 \end{gathered}$$

所以：

$$a=BC,\sin A={\displaystyle \frac{CH}{AC}},b=AC,\sin B={\displaystyle \frac{CH}{CB}}$$

可得：

$$({\displaystyle \frac{a}{\sin A}}{)}^2={\displaystyle \frac{[(x-c{)}^2+y^2](x^2+y^2)}{y^2}}=({\displaystyle \frac{b}{\sin B}}{)}^2$$

所以：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}$$

同理可得：

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{a}{\sin A}}$$

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{b}{\sin B}}$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

第五种 外接圆法一

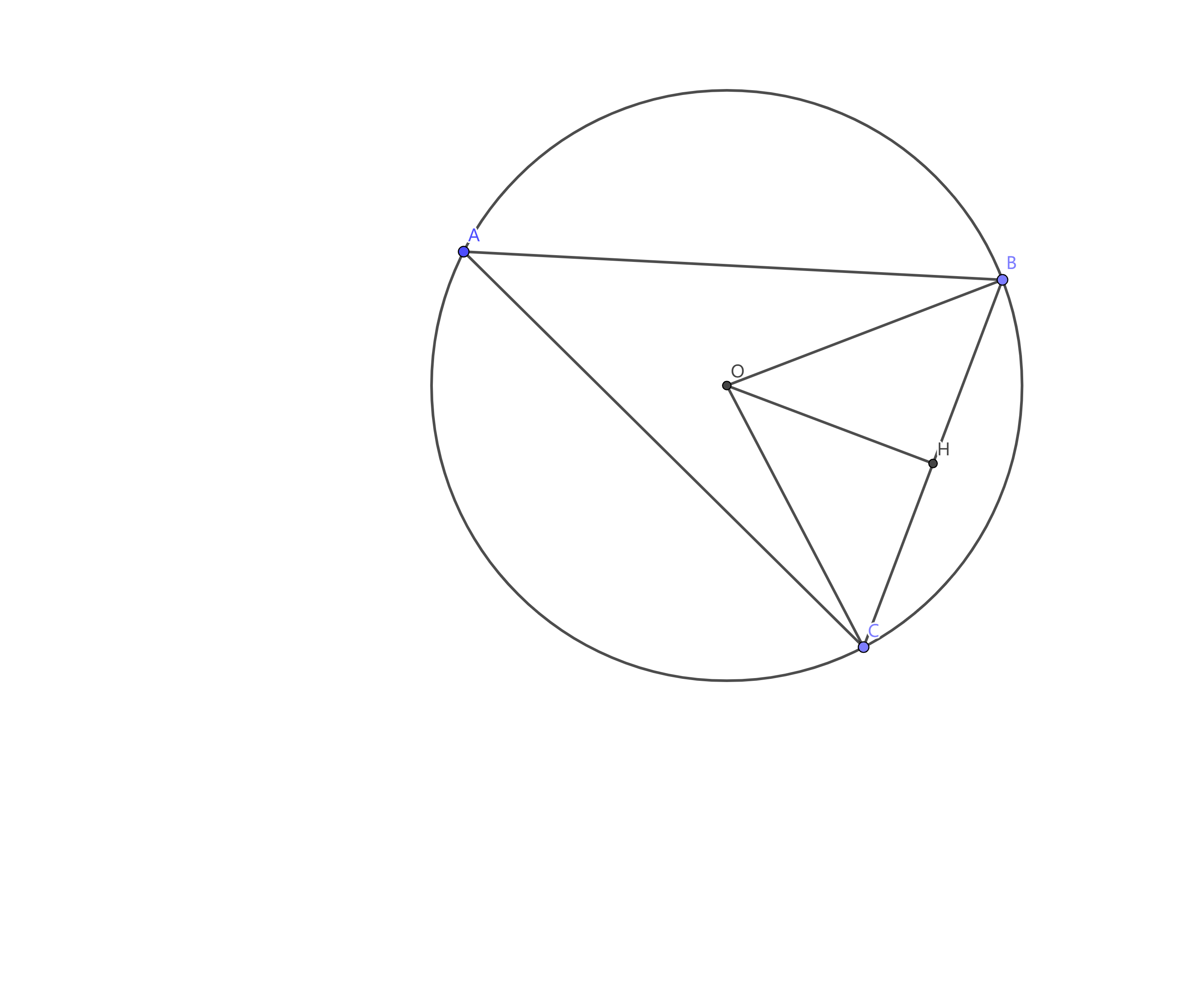
过点 $O$ 作线段 $OH\perp BC$ 交 $BC$ 于点 $H$ ，易得： $BC=a,BD={\displaystyle \frac{a}{2}}$

所以

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{a}{\sin \mathrm{\angle }BOD}}={\displaystyle \frac{a}{\frac{a}{2r}}}=2r$$

同理可得：

$${\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}=2r$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}=2r$$

第六种 外接圆法二

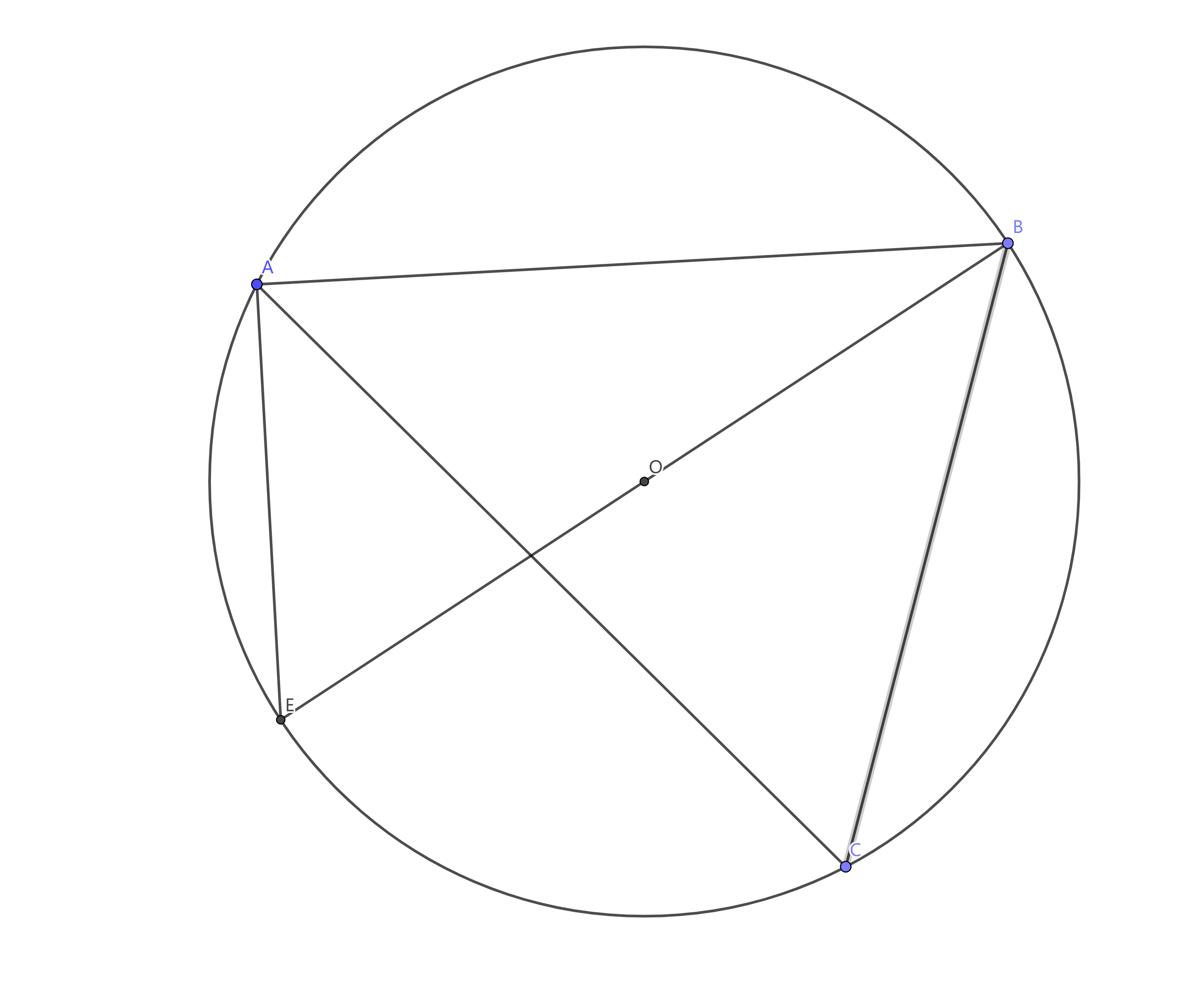
由题： $\mathrm{\angle }ACB=\mathrm{\angle }AEB$ ，所以 $\sin C=\sin \mathrm{\angle }AEB={\displaystyle \frac{AB}{EB}}={\displaystyle \frac{c}{2r}}$

所以

$${\displaystyle \frac{c}{\sin C}}=2r$$

同理可得：

$${\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{a}{\sin A}}=2r$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}=2r$$

第七种 相似法

这种正法好无聊，相当复杂，纯属拓宽思路

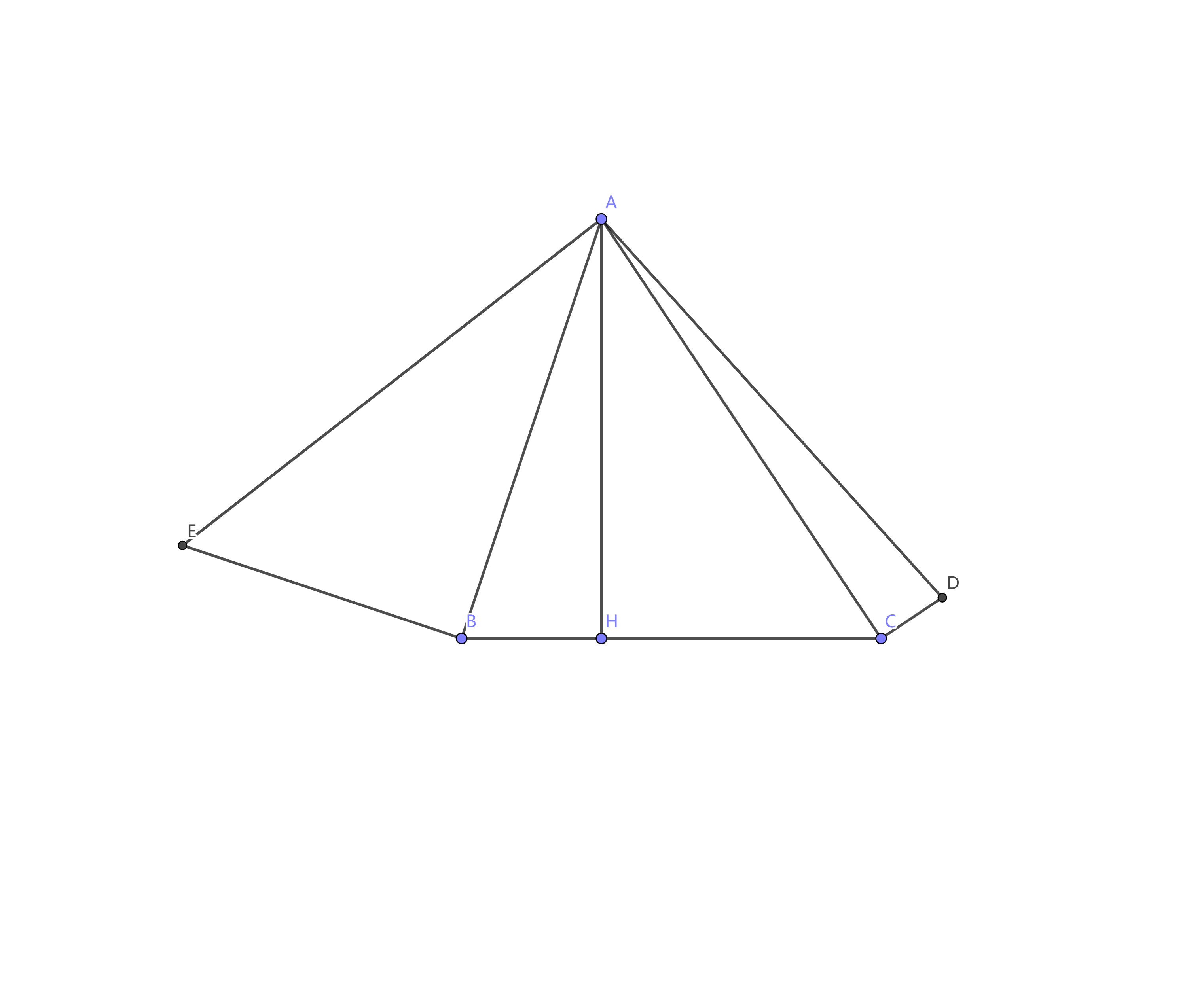
过点 $A$ 作 $AH\perp BC$ 交 $BC$ 于点 $H$.

作 $\mathrm{△}ACD\sim \mathrm{△}AHB，\mathrm{△}AHC\sim \mathrm{△}ABE$ ，可得： $\mathrm{\angle }HAC=\mathrm{\angle }EAB,\mathrm{\angle }HEB=\mathrm{\angle }CAD$ .

所以：

$${\displaystyle \frac{AE}{AC}}={\displaystyle \frac{AB}{AH}},{\displaystyle \frac{AD}{AB}}={\displaystyle \frac{AC}{AH}}\Rightarrow {\displaystyle \frac{AD}{AC}}={\displaystyle \frac{AE}{AC}}$$

所以 $AD=AE$

又因为：

$${\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{AC}{\sin \mathrm{\angle }ADC}}=AD,{\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{AB}{\sin \mathrm{\angle }AEB}}=AE$$

所以：

$${\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

同理可得：

$${\displaystyle \frac{c}{\sin C}}={\displaystyle \frac{a}{\sin A}}$$

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

第八种 向量法

这个比我发明的第七种证法还无聊，但这是教科书上的

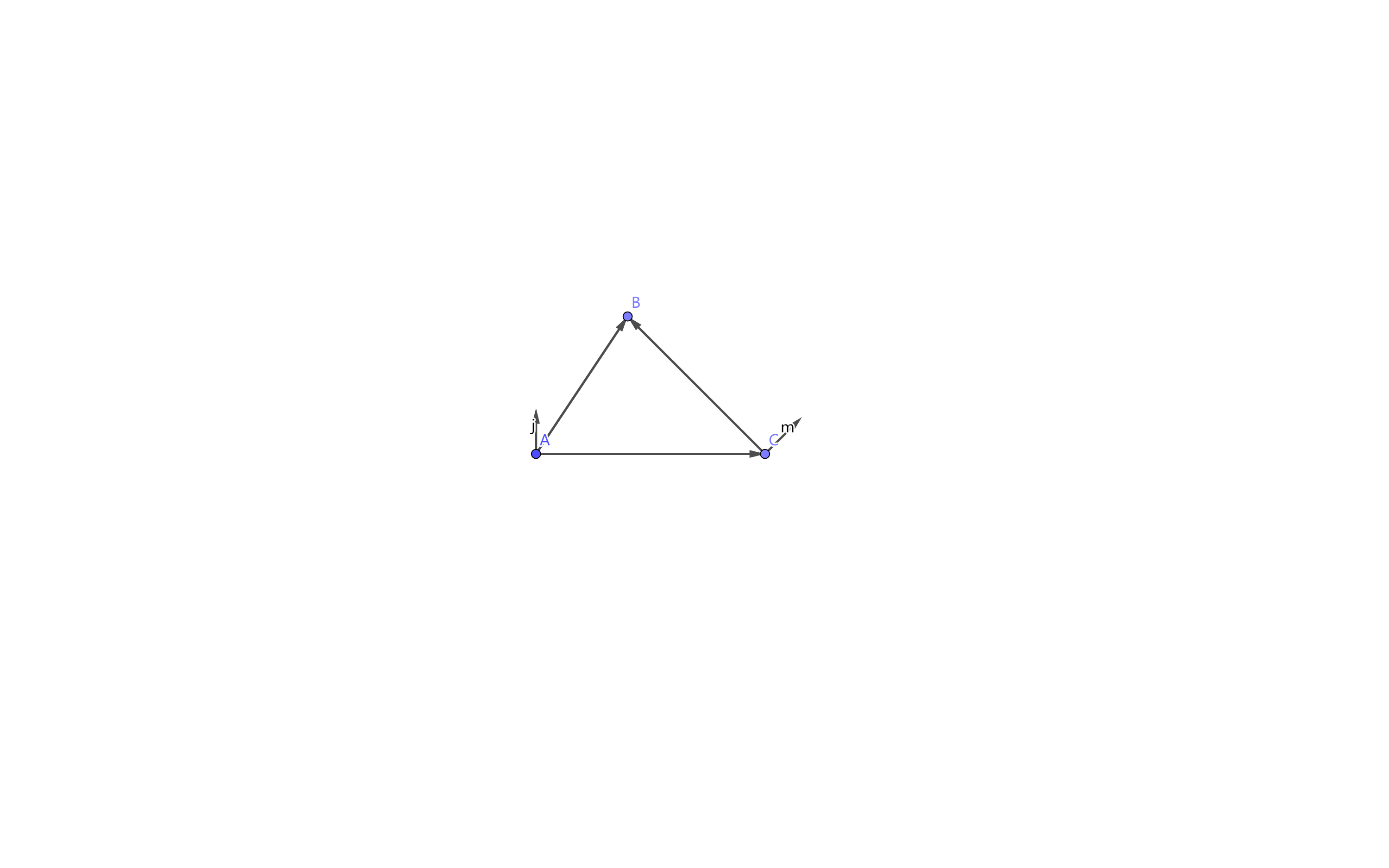
过点 $A$ 作与 $\overrightarrow{AC}$ 垂直的单位向量 $\mathit{j}$ ，则 $\mathit{j}$ 与 $\overrightarrow{AB}$ 的夹角为 ${\displaystyle \frac{\pi }{2}}-A$ ， $\mathit{j}$ 与 $\overrightarrow{CB}$ 的夹角为 ${\displaystyle \frac{\pi }{2}}-C.$
因为 $\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$ ，所以：

$$\mathit{j}\cdot (\overrightarrow{AC}+\overrightarrow{CB})=\mathit{j}\cdot \overrightarrow{AB}$$

由分配律得：

$$\mathit{j}\cdot \overrightarrow{AC}+\mathit{j}\cdot \overrightarrow{CB}=\mathit{j}\cdot \overrightarrow{AB}$$

即

$$|\mathit{j}||\overrightarrow{AC}|\cos {\displaystyle \frac{\pi }{2}}+|\mathit{j}||\overrightarrow{CB}|\cos ({\displaystyle \frac{\pi }{2}}-C)=|\mathit{j}||\overrightarrow{AB}|\cos ({\displaystyle \frac{\pi }{2}}-A)$$

也即

$$a\sin C=c\sin A\Rightarrow {\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{c}{\sin C}}$$

同理可得：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}$$

$${\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$

综上：

$${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}$$