[ APIO 2015 ] 雅加达的摩天楼

\(\\\)

\(Description\)

---

有\(N\)栋楼和\(M\)条狗，每条狗都有自己的初始地点\(p_i\)和跳跃距离\(k_i\)，每条狗每次移动只能移动到当前坐标\(\pm k_i\)的地方。

现在\(0\)号狗处有一条信息，它要传给\(1\)号狗。只有当前掌握信息的狗可以移动，在楼处狗之间可以交接，求将信息传给\(1\)号总共最少需要跳跃多少次。

• \(N,M\in [1,3\times 10^4]\)

\(\\\)

\(Solution\)

---

洛谷数据有毒

考虑暴力，直接通过每一个狗将其起点连接上所有通过该狗可以到达的地点，代价就是跳的次数，然后最短路。

好了现在你在洛谷能过了 而且这比所谓正解快的不止两倍......

显然边数是爆炸的，所以考虑优化建边。注意到如果给出的每一栋楼处都有一个\(k_i=1\)的狗，那边数就是\(N^2\)的。

注意到这样的边每一条都重建了很多次，我们不妨直接拆点，把一张符合限制的"完全图建出来"。

把每个点拆成\(k\)个点，第\(i\times k+j\)个点就代表第\(i\)个点一只\(k_i=j\)的狗处。那么如果把一个点拆出的点排在一列，那么同一行的点之间移动是自由的，如下图(发现一个生动的说法，相同层数的狗可以在高空乱JB走)边为双向：

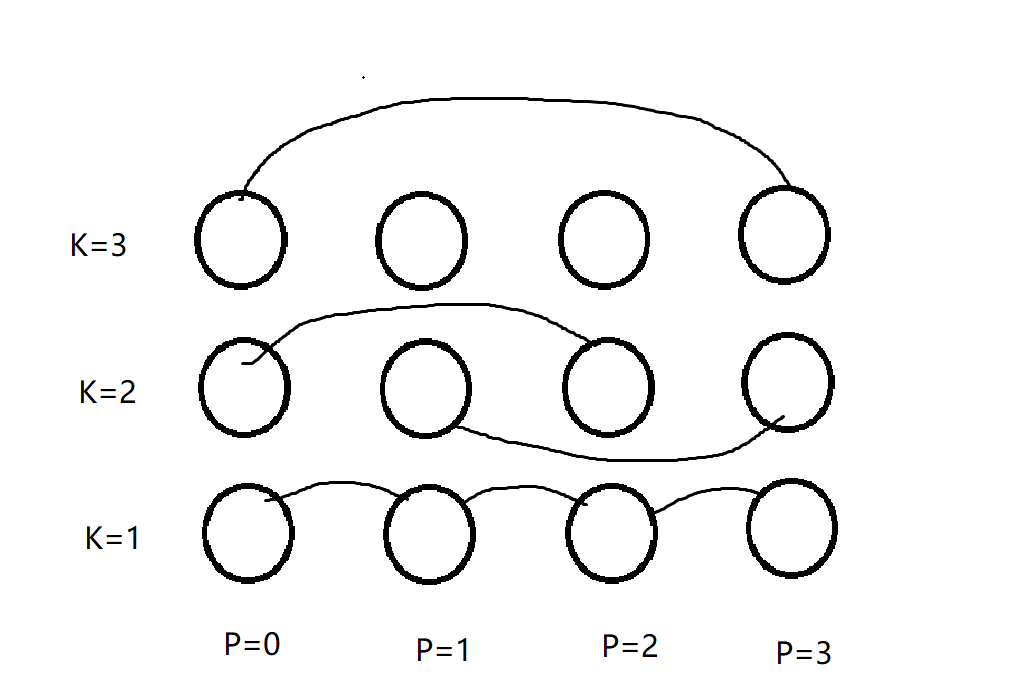
同时为了保证可以在任意处换狗，从高层下来到原始节点也连一条边，边权为\(0\)。

然后考虑狗的出现，有一条狗在\(p_i\)代表从\(p_i\)的原始节点可以上到高度为\(k_i\)层的位置，也直接连一条\(0\)边。

再考虑\(k_i\)特别大的情况，会无意义的建立了很大的一个图。

运用均值不等式的思想，进行阈值优化。只对\(\le \sqrt N\)的高度部分暴力建立新图，剩下的部分暴力建边，根据经典的分析边的级别都是\(N\sqrt N\)的，于是可以愉快的最短路了。

\(\\\)

\(Code\)

---

这题洛谷数据有毒......根号作为上界一直过不了，看了题解发现可以通过取\(min\)的方式控制上限，一路试过来发现上限为\(1\)的时候竟然最快......这不就是暴力吗......

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 30010
#define M 7000010
#define R register
#define gc getchar
#define inf 1000000000
using namespace std;

bool vis[M];

int n,m,lim=170,s,t,tot,hd[M],dis[M];

struct edge{int w,to,nxt;}e[M<<1];

inline void add(int u,int v,int w){
  e[++tot].to=v; e[tot].w=w;
  e[tot].nxt=hd[u]; hd[u]=tot;
}

inline int pos(int p,int h){return p*(lim+1)+h;}

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

queue<int> q;

inline void spfa(){
  int totp=pos(n,lim);
  for(R int i=0;i<=totp;++i) dis[i]=inf;
  dis[s]=0; q.push(s);
  while(!q.empty()){
    int u=q.front();
    q.pop(); vis[u]=0;
    for(R int i=hd[u],v;i;i=e[i].nxt)
      if(dis[v=e[i].to]>dis[u]+e[i].w){
        dis[v]=dis[u]+e[i].w;
        if(!vis[v]) q.push(v),vis[v]=1;
      }
  }
}

int main(){
  n=rd(); m=rd();
  for(R int i=0;i<n;++i)
    for(R int j=1;j<=lim;++j) add(pos(i,j),pos(i,0),0);
  for(R int i=0;i<n;++i)
    for(R int j=1;j<=lim;++j)
      if(i+j<n){add(pos(i,j),pos(i+j,j),1);add(pos(i+j,j),pos(i,j),1);}
  for(R int i=1,p,k;i<=m;++i){
    p=rd(); k=rd();
    if(i==1) s=pos(p,0);
    if(i==2) t=pos(p,0);
    if(k<=lim) add(pos(p,0),pos(p,k),0);
    else{
      for(R int j=1;p+j*k<n;++j) add(pos(p,0),pos(p+j*k,0),j);
      for(R int j=1;p-j*k>=0;++j) add(pos(p,0),pos(p-j*k,0),j);
    }
  }
  spfa(); printf("%d",(dis[t]<inf)?dis[t]:-1);
  return 0;
}