[ USACO 2007 FEB ] Lilypad Pond (Gold)
\(\\\)
\(Description\)
一张\(N\times M\)的网格，已知起点和终点，其中有一些地方是落脚点，有一些地方是空地，还有一些地方是坏点。
现在要从起点到终点，每次移动走日字\((\)横一纵二或横二纵一\()\)，其中只能经过起点、终点、落脚点。
现在可以开发任意个数的空地变为落脚点，问找到合法路径最少需要开发多少个空地，以及最少开发的方案数。
注意，只要有一个被开发的空地不同即视为不同的方案。
- \(N,M\in [1,30]\)
\(\\\)
\(Solution\)
不得不说建图相当妙。
先考虑一种直接的建图方式，落脚点和起点向可以直接到达的空地或落脚点连\(0\)边，空地向可以直接到达的空地或落脚点连\(1\)边，最短路计数。我们发现这样的最短路长度是没有问题的，但是最短路方案数是有问题的。
因为像这样，在两个空地之间可以有多个可以用于转移的原有落脚点时，方案数就会多算好几倍。
\(\\\)
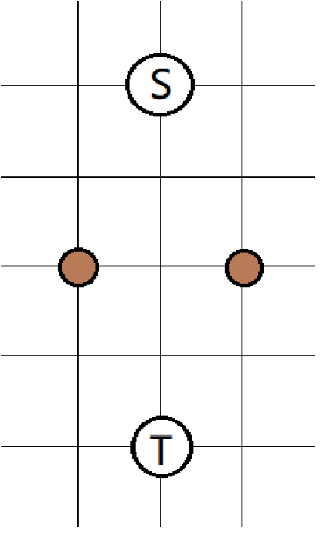
然后发现，貌似中间经过已有的落脚点不同并不会影响两点间的最短路长度和计数，所以不妨直接忽略掉所有原有的落脚点以及坏点，只考虑包含起点、终点、空地的图，以下将起点终点视为空地。
建图可以对每一个合法的点\(BFS\)一遍，统计出该点在经过若干个\((\)可以不经过\()\)原有落脚点可以到达的空地，显然中间经过落脚点是没有代价的，而在开始\(BFS\)的点处需要花费代价建造落脚点，所以边权为\(1\)。特殊的，起点并不需要代价，所以起点连出去的边边权为\(0\)。此时最短路条数显然就是方案数了。
\(\\\)
\(Code\)
最短路计数又傻了....注意不是加一而是累加，以及重置的时候不是\(1\)，而是直接继承
注意边表的大小需要开 long long 差评
#include<cmath>
#include<queue>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 50
#define M 60010
#define R register
#define gc getchar
#define inf 200000000
using namespace std;
typedef long long ll;
inline int rd(){
int x=0; bool f=0; char c=gc();
while(!isdigit(c)){if(c=='-')f=1;c=gc();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return f?-x:x;
}
bool vis[N*N];
const int dx[8]={1,1,-1,-1,2,2,-2,-2};
const int dy[8]={2,-2,2,-2,1,-1,1,-1};
ll ts[N*N];
int n,m,s,t,tot,dis[N*N];
int cnt,num[N][N],mp[N][N],hd[N*N];
struct edge{int w,to,nxt;}e[M<<1];
inline void add(int u,int v,int w){
e[++tot].to=v; e[tot].w=w;
e[tot].nxt=hd[u]; hd[u]=tot;
}
queue<pair<int,int> > q;
inline void bfs(int ux,int uy,int w){
memset(vis,0,sizeof(vis));
q.push(make_pair(ux,uy)); vis[num[ux][uy]]=1;
while(!q.empty()){
int x=q.front().first;
int y=q.front().second; q.pop();
for(R int i=0,nx,ny;i<8;++i){
nx=x+dx[i]; ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m||vis[num[nx][ny]]) continue;
vis[num[nx][ny]]=1;
if(mp[nx][ny]!=1&&mp[nx][ny]!=2) add(num[ux][uy],num[nx][ny],w);
else if(mp[nx][ny]==1) q.push(make_pair(nx,ny));
}
}
}
queue<int> qs;
inline void SPFA(){
memset(vis,0,sizeof(vis));
for(R int i=1;i<=cnt;++i) dis[i]=inf;
qs.push(s); dis[s]=0; ts[s]=1ll;
while(!qs.empty()){
int u=qs.front();
qs.pop(); vis[u]=0;
for(R int i=hd[u],v;i;i=e[i].nxt)
if(dis[v=e[i].to]>dis[u]+e[i].w){
dis[v]=dis[u]+e[i].w; ts[v]=ts[u];
if(!vis[v]) vis[v]=1,qs.push(v);
}
else if(dis[v]==dis[u]+e[i].w) ts[v]+=ts[u];
}
}
int main(){
n=rd(); m=rd();
for(R int i=1;i<=n;++i)
for(R int j=1;j<=m;++j){
mp[i][j]=rd();
num[i][j]=++cnt;
if(mp[i][j]==3) s=cnt;
if(mp[i][j]==4) t=cnt;
}
for(R int i=1;i<=n;++i)
for(R int j=1;j<=m;++j)
if(mp[i][j]==0||mp[i][j]>1) bfs(i,j,(mp[i][j]!=3));
SPFA();
if(dis[t]<inf) printf("%d\n%lld",dis[t],ts[t]);
else puts("-1");
return 0;
}
