[ USACO 2007 OPEN ] Dining
\(\\\)
\(Description\)
有\(N\)头牛,\(F\)种食物,\(D\)种饮料,每种食物和饮料只有一份。
现在已知每头牛可以吃哪些食物,可以喝哪些饮料,问最多可以让多少头牛可以同时得到喜欢的食物和饮料。
- \(N,F,D\in [1,100]\)
\(\\\)
\(Solution@\)二分图
这是一个最大匹配问题,但是需要两侧同时满足可以增广,有一侧不合法就不计入答案。
直接两侧分别做一次匈牙利是有问题的。如果一侧匹配上了,另一侧没有,那么其实在\(DFS\)的过程中已经将某一侧的匹配对象改变了,进而可能会导致下一步其他元素在匹配的时候匹配不上。
于是我们在每次增广之前先备份一份\(match\)数组,如果出现了一侧匹配一侧不匹配的情况就将\(match\)数组还原。
\(\\\)
\(Code\)
出锅了...\(Luogu\)上一道几乎一样的题交了就过了,但是这道题一直\(80\)。
下了一波数据发现好像是有的牛没有喜欢的食物和饮料的锅....
然后把这种情况算成合法又有一个点跪了...那个点里好像这种情况又不算做合法了...
还是没有想懂网络流为啥过了...网络流做似乎并没有将这种特殊点算作合法...大爷们找到原因麻烦告诉我一声...
#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 110
#define R register
#define gc getchar
using namespace std;
inline int rd(){
int x=0; bool f=0; char c=gc();
while(!isdigit(c)){if(c=='-')f=1;c=gc();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return f?-x:x;
}
int n,f,d,ans,tot1,hd1[N],tot2,hd2[N];
int m1[N],m2[N],vis1[N],vis2[N],tmp1[N],tmp2[N];
struct edge{int to,nxt;}e1[N*N],e2[N*N];
inline void add1(int u,int v){
e1[++tot1].to=v; e1[tot1].nxt=hd1[u]; hd1[u]=tot1;
}
inline void add2(int u,int v){
e2[++tot2].to=v; e2[tot2].nxt=hd2[u]; hd2[u]=tot2;
}
inline bool dfs1(int u,int t){
for(R int i=hd1[u],v;i;i=e1[i].nxt)
if(vis1[v=e1[i].to]!=t){
vis1[v]=t;
if(!m1[v]||dfs1(m1[v],t)){m1[v]=u;return 1;}
}
return 0;
}
inline bool dfs2(int u,int t){
for(R int i=hd2[u],v;i;i=e2[i].nxt)
if(vis2[v=e2[i].to]!=t){
vis2[v]=t;
if(!m2[v]||dfs2(m2[v],t)){m2[v]=u;return 1;}
}
return 0;
}
int main(){
n=rd(); f=rd(); d=rd();
for(R int i=1,x,y;i<=n;++i){
x=rd(); y=rd();
for(R int j=1,v;j<=x;++j){v=rd();add1(i,v);}
for(R int j=1,v;j<=y;++j){v=rd();add2(i,v);}
}
for(R int i=1;i<=n;++i){
for(R int j=1;j<=f;++j) tmp1[j]=m1[j];
for(R int j=1;j<=d;++j) tmp2[j]=m2[j];
if(dfs1(i,i)&&dfs2(i,i)) ++ans;
else{
for(R int j=1;j<=f;++j) m1[j]=tmp1[j];
for(R int j=1;j<=d;++j) m2[j]=tmp2[j];
}
}
printf("%d\n",ans);
return 0;
}
\(\\\)
\(Solution@\)网络流
这是一个最大流问题,考虑有两个限制同时满足才可以将一个点视为合法,所以建图考虑将限制分别放在牛的两侧,容量都为\(1\),这样答案就转化成了最大流。
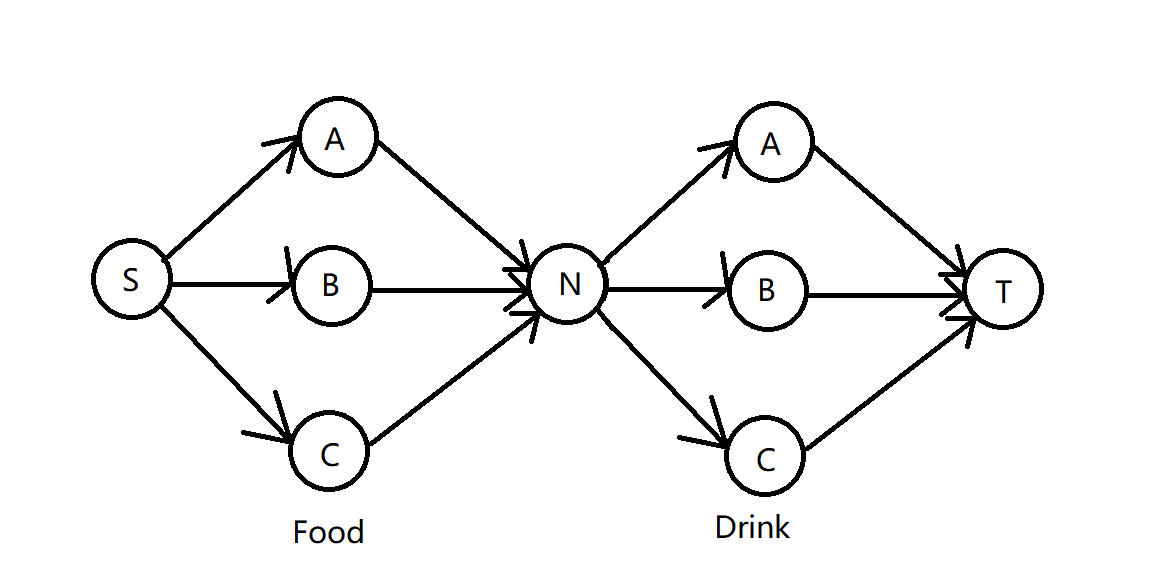
有一种情况需要特殊考虑,如下图,最大流是\(3\),实际上答案是\(1\),因为忽视了每头牛的贡献最多为\(1\)的限制。
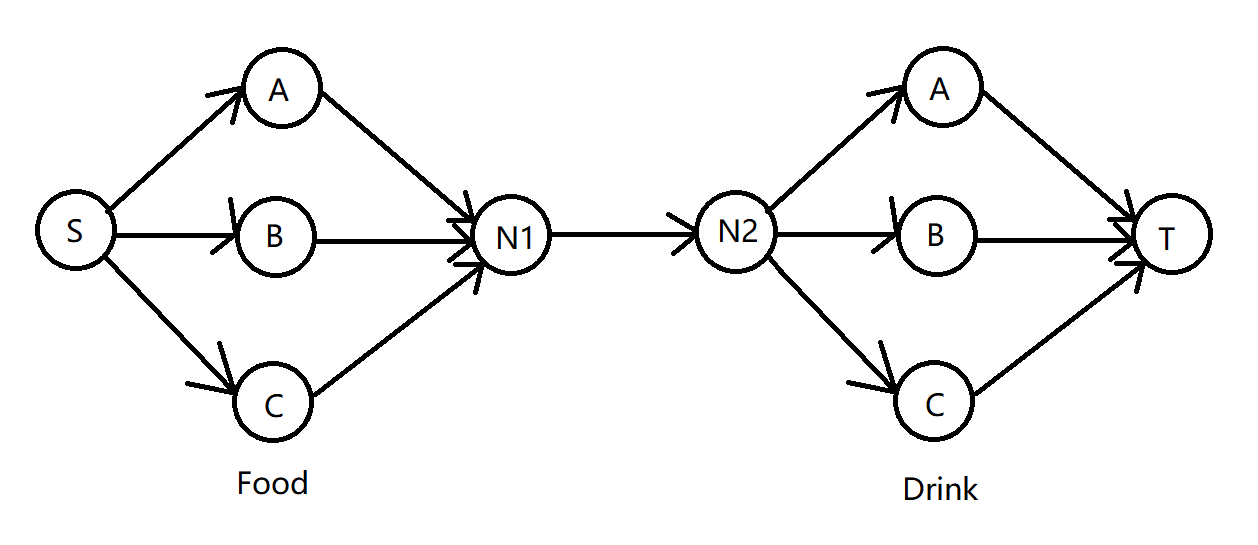
于是有一个机智的做法,将每一个牛都拆成两个点,连一条容量为\(1\)的边,这样每个牛最多只会允许一支流通过。
\(\\\)
\(Code\)
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10100
#define R register
#define gc getchar
#define inf 200000000
using namespace std;
inline int rd(){
int x=0; bool f=0; char c=gc();
while(!isdigit(c)){if(c=='-')f=1;c=gc();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return f?-x:x;
}
int n,m1,m2,cnt,f[N],l[N],r[N],c[N];
int s,t,tot=1,hd[N],h[N],dp[N];
struct edge{int w,to,nxt;}e[N*100];
inline void add(int u,int v,int w){
e[++tot].to=v; e[tot].w=w;
e[tot].nxt=hd[u]; hd[u]=tot;
}
queue<int> q;
inline bool bfs(){
for(R int i=0;i<=cnt;++i) dp[i]=0;
dp[s]=1; q.push(s);
while(!q.empty()){
int u=q.front(); q.pop();
for(R int i=hd[u],v;i;i=e[i].nxt)
if(e[i].w&&(!dp[v=e[i].to])){
dp[v]=dp[u]+1; q.push(v);
}
}
return dp[t]>0;
}
inline int dfs(int u,int flow){
if(u==t||!flow) return flow;
int res=0,tmp;
for(R int &i=h[u];i;i=e[i].nxt)
if(e[i].w&&(dp[e[i].to]==dp[u]+1)){
tmp=dfs(e[i].to,min(e[i].w,flow-res));
e[i].w-=tmp; e[i^1].w+=tmp; res+=tmp;
if(res==flow) return res;
}
return res;
}
inline int dinic(){
int res=0;
while(bfs()){
for(R int i=0;i<=cnt;++i) h[i]=hd[i];
res+=dfs(s,inf);
}
return res;
}
int main(){
n=rd(); m1=rd(); m2=rd();
for(R int i=1;i<=m1;++i) f[i]=++cnt;
for(R int i=1;i<=n;++i) l[i]=++cnt,r[i]=++cnt;
for(R int i=1;i<=m2;++i) c[i]=++cnt;
s=0; t=++cnt;
for(R int i=1;i<=m1;++i){add(s,f[i],1);add(f[i],s,0);}
for(R int i=1;i<=n;++i){add(l[i],r[i],1);add(r[i],l[i],0);}
for(R int i=1;i<=m2;++i){add(c[i],t,1);add(t,c[i],0);}
for(R int i=1,a,b,x;i<=n;++i){
a=rd(); b=rd();
for(R int j=1;j<=a;++j){
x=rd(); add(f[x],l[i],1); add(l[i],f[x],0);
}
for(R int j=1;j<=b;++j){
x=rd(); add(r[i],c[x],1); add(c[x],r[i],0);
}
}
printf("%d\n",dinic());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号