[ Luogu 3398 ] 仓鼠找sugar

\(\\\)

\(Description\)

---

给出一棵\(N\)个节点的树，\(K\)次询问从\(A_i\)到\(B_i\)的最短路径，与从\(C_i\)到\(D_i\)的最短路径是否有交。

• \(N,K\in [1,10^5]\)

\(\\\)

\(Solution\)

---

• 倍增\(Lca\)板子。注意到树形结构不会出现环，所以如果有交必然有一个\(Lca\)在另一个\(Lca\)到产生它的两个节点的路径之一上。用画图形象化的表示：

  

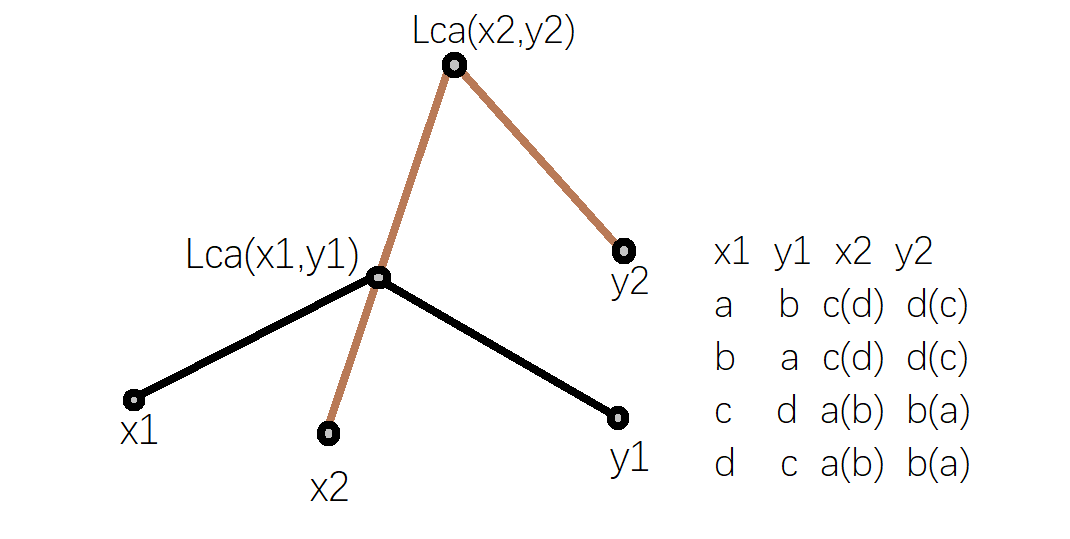
  图上已经标出了四种\((\)八种\()\)可能的情况。

• 然后就判一波\(Lca\)之间的关系就好，假设要判断点\(m\)是否在从\(l\)到\(r\)的路径上，其中\(r\)是\(l\)的祖先，则成立条件就是\(Lca(l,m)=m\)并且\(deep_m>deep_r\)。

\(\\\)

\(Code\)

---

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 100010
#define R register
#define gc getchar
using namespace std;

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

int n,m,t,tot,d[N],hd[N],f[N][20];
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v){
  e[++tot].to=v; e[tot].nxt=hd[u]; hd[u]=tot;
}

queue<int> q;
inline void bfs(){
  q.push(1); d[1]=1;
  while(!q.empty()){
    int u=q.front(); q.pop();
    for(R int i=hd[u],v;i;i=e[i].nxt)
      if(!d[v=e[i].to]){
        d[v]=d[u]+1; f[v][0]=u;
        for(R int j=1;j<=t;++j) f[v][j]=f[f[v][j-1]][j-1];
        q.push(v);
      }
  }
}

inline int lca(int u,int v){
  if(d[u]>d[v]) u^=v^=u^=v;
  for(R int i=t;~i;--i) if(d[f[v][i]]>=d[u]) v=f[v][i];
  if(u==v) return u;
  for(R int i=t;~i;--i) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
  return f[u][0];
}

inline bool valid(int m,int l,int r){return (lca(m,l)==m&&d[m]>=d[r]);}

inline bool check(int a,int b,int c,int d){
  int l1=lca(a,b),l2=lca(c,d);
  return (valid(l2,a,l1)||valid(l2,b,l1)||valid(l1,c,l2)||valid(l1,d,l2));
}

int main(){
  t=log2(n=rd())+1; m=rd();
  for(R int i=1,u,v;i<n;++i){
    u=rd(); v=rd(); add(u,v); add(v,u);
  }
  bfs();
  for(R int i=1,a,b,c,d;i<=m;++i){
    a=rd(); b=rd(); c=rd(); d=rd();
    puts(check(a,b,c,d)?"Y":"N");
  }
  return 0;
}