曼哈顿距离与切比雪夫距离的互化

\(\\\)

曼哈顿距离

---

对于两个点\((x_1,y_1),(x_2,y_2)\)，定义他们的曼哈顿距离为\(|x_1-x_2|+|y_1-y_2|\)，即两坐标轴分别讨论差值再求和。

对于曼哈顿距离相同的点，他们分布在同一横纵截距且截距相同的直线上。

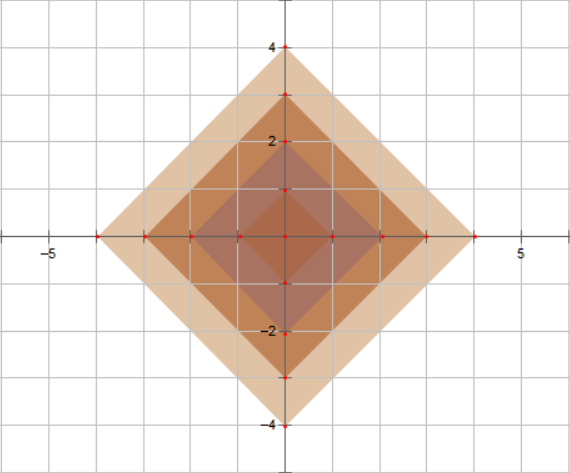
图中每一个正方形边界上的整点到原点的曼哈顿距离相同。

\(\\\)

切比雪夫距离

---

对于两个点\((x_1,y_1),(x_2,y_2)\)，定义他们的曼哈顿距离为\(max\{|x_1-x_2|,|y_1-y_2|\}\)，即两坐标轴分别讨论差值取最大。

对于切比雪夫距离相同的点，他们分布在以原点为中心的正方形边界上。

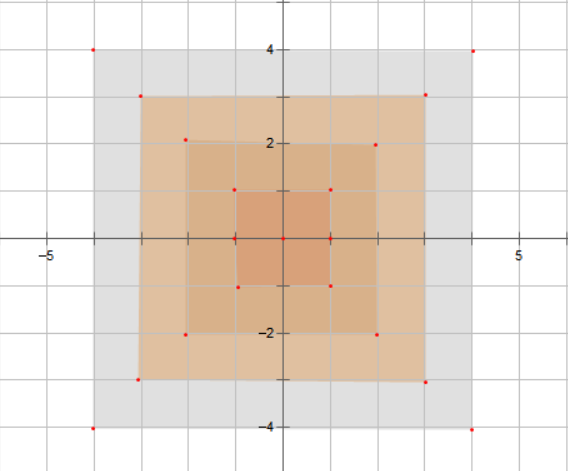
图中每一个正方形边界上的整点到原点的曼哈顿距离相同。

\(\\\)

曼哈顿距离转切比雪夫距离

---

考虑曼哈顿距离的表达式：\(|x_1-x_2|+|y_1-y_2|\)，其实可以表示成：

\(\begin{align}max\{x_1-x_2+y_1-y_2,x_1-x_2+y_2-y_1,x_2-x_1+y_1-y_2,x_2-x_1+y_2-y_1\}\end{align}\)

考虑将两个点变化为\((x_1+y_1,x_1-y_1),(x_2+y_2,x_2-y_2)\)

那么变化后两点的切比雪夫距离为\(max((|(x_1+y_1)-(x_2+y_2)|,|(x_1-y_1)-(x_2-y_2)|)\)

若原来两点曼哈顿距离为\(x_1-x_2+y_1-y_2\)或\(x_2-x_1+y_2-y_1\)时，都可以表示为\(|(x_1+y_2)-(x_2+y_2)|\)

若原来两点曼哈顿距离为\(x_1-x_2+y_2-y_1\)或\(x_2-x_1+y_1-y_2\)时，都可以表示为\(|(x_1-y_1)-(x_2-y_2)|\)

将每一个点\((x,y)\)转化为\((x+y,x-y)\)，新坐标系下的切比雪夫距离即为原坐标系下曼哈顿距离。

\(\\\)

切比雪夫距离转曼哈顿距离

---

按照刚才的思路再还原回去即可。

将每一个点\((x,y)\)转化为\((\frac{x+y}{2},\frac{x-y}{2})\)，新坐标系下的曼哈顿距离即为原坐标系下切比雪夫距离。

这个转化一般比较常用，曼哈顿距离一般可以通过排序前缀和的方式降低计算复杂度。

注意到除法如果向下取整可能会使答案不正确，所以考虑先不除以\(2\)，最后求完答案再除以\(2\)也是一样的，形象的理解可以说成，曼哈顿坐标系是通过切比雪夫坐标系旋转\(45^{\circ}\)后，再缩小到原来的一半得到的。

\(\\\)

一道例题

---

有\(N\)个二位平面上的点，定义每一个点到其八连通的点的距离为\(1\)。

选一个点，使得剩下所有点到该点的距离之和最小，求出这个距离之和。

• \(N\in [0,10^5]\)

\(\\\)

题意即为求切比雪夫距离之和最小，暴力的做法是\(N^2\)的。

考虑将切比雪夫距离转化为曼哈顿距离，我们将横纵坐标分开排序求前缀和，这样既可快速求出，以一个点为中心，其他点到这个点的曼哈顿距离之和。

具体的做法是将两个坐标分开讨论，每次找到当前点在排序后数组的位置\(p\)。

那么它前面的点坐标都小于当前点，累加的答案为\(p\times x[i]-sum_p\)。

后面的点的坐标都大于当前点，反过来累加答案，为\((sum_n-sum_p)-(n-p)\times x[i]\)

对所有的点都求一遍，取最小值即可，复杂度\(\text O(NlogN)\)。

\(\\\)

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 100010
#define R register
#define gc getchar
#define inf 900000000000000000
using namespace std;
typedef long long ll;

inline ll rd(){
  ll x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

ll n,ans=inf,x[N],y[N],sx[N],sy[N],sumx[N],sumy[N];

int main(){
  n=rd();
  for(R ll i=1,xx,yy;i<=n;++i){
    xx=rd(); yy=rd();
    sx[i]=x[i]=xx+yy; sy[i]=y[i]=xx-yy;
  }
  sort(sx+1,sx+1+n);
  sort(sy+1,sy+1+n);
  for(R ll i=1;i<=n;++i){
    sumx[i]=sumx[i-1]+sx[i];
    sumy[i]=sumy[i-1]+sy[i];
  }
  for(R ll i=1,res;i<=n;++i){
    ll px=lower_bound(sx+1,sx+1+n,x[i])-sx;
    ll py=lower_bound(sy+1,sy+1+n,y[i])-sy;
    res=px*x[i]-sumx[px]+sumx[n]-sumx[px]-(n-px)*x[i];
    res+=py*y[i]-sumy[py]+sumy[n]-sumy[py]-(n-py)*y[i];
    ans=min(ans,res>>1);
  }
  printf("%lld\n",ans);
  return 0;
}