『联合省选2025集训』『图的连通性进阶』Day3 略解

前言

我们趋行在人生这个亘古的旅途，在坎河中奔跑，在挫折里涅槃，忧愁缠满全身，痛苦飘洒一地。我们累，却无从止歇；我们苦，却无法回避。

今天是连通性的进阶题目，重点是耳分解，双极定向，以及边三连通分量。

因为调题速度过慢，导致被硬控，所以第二天晚上补的差不多了再来写的。

感觉知识点方面也需要写个东西稍微总结一下，看周末有没有时间和心情吧。

A

简单来说，就是选择边权最小的边让原图满足点双连通。

可以发现，这个边权最小的点双连通实际上就是从最开始一个单独的点，一直加相对于当前的点集的开耳，直到整个图上的点都被加进去，然后保证边权和最小。

显然有一个状压 \(\texttt{DP}\)，定义 \(dp_S\) 表示当前点集 \(S\)，构成一个点双所需要的最小边权。转移的话就是一直向点集 \(S\) 里加相对于它的开耳，直接枚举这个开耳的点集，然后预处理出这个点集形成开耳所需要的最小边权即可，时间复杂度应该是 \(\mathcal{O}(3^n\times \text{polylog}(n))\)。

其实可以考虑稍微优化一下，即不是每次一次性的将整个开耳加进去，而是一个点一个点的加。

即定义 \(dp_{S,i,j}\) 表示上一个加入开耳的点是 \(i\)，这个开耳的最后一个点是 \(j\)，现在加入开耳的点的集合是 \(S\)。直接枚举 \((i,k)\) 转移，然后当你又一次回到点 \(j\) 的时候，稍微处理一下下一个新开耳的信息就可以了。时间复杂度 \(\mathcal{O}(2^n\times \text{polylog}(n))\)。

需要非常注意重边的情况，比如 \(x\to y\to x\) 这种开耳，你就需要在第二次加入 \(y\to x\) 这条边的时候，边权和计算的应该是 \((x,y)\) 之间所有的重边次小的那一个，因为最小的在 \(x\to y\) 已经被使用了。

我的实现是 \(\mathcal{O}(2^n\times n^3)\) 的。

\(\texttt{Code}\)

B

以前应该做过，但是我再看一遍之后貌似还是不会。

首先，不妨设 \(a\le b\le c\)，找一下数量关系，那么显然有：\(c\ge \frac{n}{3},a\le b\le \frac{n}{2}\)。

另外，我们只需要考虑联通的导出子图点集大小分别为 \(a,b\) 的情况，因为如果你凑出了是 \(c\) 的，那么你可以删点得到 \(a/b\)。

观察特殊性质，发现有一档 \(m=n-1\)，所以我们先来思考一些树的情况怎么解决。

本质上就是找到一条边 \((x,y)\) 满足 \(x\) 那边的点的个数 \(\ge a\)，\(y\) 那边的点的个数 \(\ge b\)。

显然可以通过遍历一次树来判断。

但是其实进一步的，我们可以通过更精确的方式来描述这个合法。

我们其实只需要考虑这个树的重心，如果它能找到一个子树的 \(a\le \text{siz} \le \frac{n}{2}\)，那么由于 \(n-\text{siz}\ge \frac{n}{2}\)，于是合法。

可以发现只要合法，就必然会存在一个方案跟重心有关，所以我们只需要关注这个重心。

考虑如何扩展到一般图。

显然，为了往树上我们刚刚的方法靠近，我们考虑弄出这个图的搜索树，并求出这个搜索树的重心。

如果这个重心已经可以做到存在一个儿子的大小 \(\ge a\) 了，那么就显然合法，按照刚刚的办法做就可以了。

考虑枚举这个重心的儿子，显然在上面的合法情况排除掉之后，有 \(\text{siz}< a\)，看从这个儿子的子树里面，经过非树边能到的其他子树。假设当前儿子是 \(x\)，可以到达 \(y_1,...y_m\) 这么多颗其他子树。（我们用重心的儿子来表示这些子树，其实就是这个子树的根）我们一直 \(\text{siz}_x+\text{siz}_{y_1}+...+\text{siz}_{y_{M}}\)，找到最小的 \(M\) 满足当前的 \(\text{siz}_x+\text{siz}_{y_1}+...+\text{siz}_{y_{M}}\ge a\)，就不加了，因为当前的显然已经够满足 \(A\) 了。可以发现，我们最多只会花费 \(2\times a\) 去满足 \(A\)，因为 \(a\le x+y_1+..y_M\le 2\times a\) 本质上还是因为 \(x,y_1,...y_M\le a\)。可以发现，\(2\times a+b\le a+b+c=n\)，故显然可以在剩下的子树中弄出 \(B\)。于是合法。

当然，如果找不到 \(M\) 能够让所有的子树能到的子树的大小之和都到不了 \(a\) 那么就显然是无解的。

注意一下输出方案的细节。

感觉思路很自然，但是我就是想不到啊啊啊。

\(\texttt{Code}\)

C

真恶心题，待会再来写。

D

边三模板题，但是当我看见我的点双和边双模板在洛谷上都没有过的时候，我的心就已经凉了半截了。

警示后人，本人试图通过类似点双的删边的方式来求边三，即我把要删的边一个一个删掉，剩下的连通块就对应一个边三，但是他是不对的！！！

简单来说就是，为了让其他的连通块分开，我们就需要删掉一些边，但这就会导致你需要的一个连通块内部联通的边被删掉，然后怎么也够不成这个连通块，具体可以看我同学知道我花费半天得出这个自然做法是错误而写的帖子。

总之，下次我做板子题一定去看别人的实现方法，我再也不乱搞了！！！

首先，先看怎样的大小为 \(\le 2\) 的割集会发挥作用。

首先是一条单独的树边，满足其是割边（也就是没有包含这条边的非树边）。
非树边+树边的组合，即包含这条树边的非树边只有当前这一条非树边。
树边+树边的组合，满足分别包含这两条树边的非树边的集合相同。

第三种情况不一定好理解，所以盗一张图片过来：

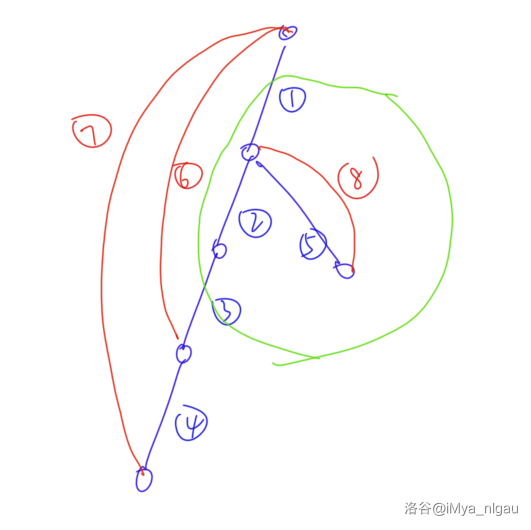
其中，蓝色是树边，红色是非树边。

然后我们发现我们需要快速计算一条树边被包含的非树边的集合，貌似不是一件很容易的时间。

这里需要用到一个 \(\text{Trick}\)。

考虑对于每条非树边随机赋一个 \([0,2^{64}-1]\) 的权值，然后定义每个点的权值表示从这个点出发的非树边的权值的异或和。

发现，若我们定义树边的权值表示一条树边被包含的非树边的权值异或和，其就是这条树边在搜索树上深度更深的端点，其子树内（包括他自己）所有的点的权值的异或和。这一步应该还是比较好理解的。

故，对于没有被非树边包含的树边，这条树边的边权显然就是 \(0\)，如果这条树边是被仅一条非树边包含，那么显然这条边的权值在非树边中也会出现。如果两条树边被包含的非树边的集合相同，等价于这两条树边的权值相同。

接下来考虑怎么求连通分量。

首先可以考虑把第一二种割集所涵盖的所有树边从搜索树上删掉（至于是哪些树边，就使用刚刚的异或哈希的技巧判断即可。），然后就会剩下若干个连通块，然后在这些连通块中分别考虑第三种割集的情况。

观察到对于所有第三种割集所对应的两条树边，我们其实只需要考虑相邻的树边，因为对于同种的配对的所有树边都在一条祖孙链上。

破防了，我要摘抄题解。

具体的，我们在 dfs 回溯的过程中维护一个 Hash 表，这样对于每条树边，我们能快速求出它下方与它配对的另一条树边，然后直接删掉两条边之间的连通块，这个连通块中一定不存在可以配对的边了，因为如果存在，也在之前的过程中删完了。这也就是说，删掉的这个连通块就是一个边三连通分量。删掉所有配对边之间部分之后，剩下的部分也是一个边三连通分量。

然后就过了。

\(\texttt{Code}\)