数学之概率题目总结
前言
如有错误，欢迎各位 dalao 指出。
前置芝士：
- 概率
T1
可以看见，标签是入门，一定非常水。
显然，要让小D获胜，我们只需要选出 \(max(v,w)\rightarrow 6\) 这一段的任意一个值即可获胜，注意特判一下 \(max(v,w)>6\) 的情况就行了。
还是比较水。
T2
老师抽我起来讲，我差点就不会讲了。。。
首先，如果当前的卡牌的红色数值大于蓝色数值，就说明以他为第一个两面数字不同的卡牌所构成的所有方案都应该算进红色的概率。而对于其他每一张卡牌来说，都是这样，所以，我们只需要将红色数值大的卡牌记录下来，为 \(red\)，再将蓝色大的卡牌记录下来，为 \(blue\) ，相同的其实完全不用考虑。（自己思考。）
红色概率就是 \(\dfrac{red}{blue+red}\)，蓝色概率就是 \(\dfrac{blue}{red+blue}\)。
可能解释的不清楚
T3
口胡结论，一遍过。
首先，先看你选中的那扇门，由于你是任意选的，所以，它背后有车的概率显然为 \(\dfrac{1}{n}\)。
而至于留下来的另一扇门，只要选中的门，背后没车，它背后就一定有车，显然概率为 \(\dfrac{n-1}{n}\)
T4
爆搜水题。
首先根据第一个字符串找出终点，然后第二个字符串直接搜索，如果遇到问号就让他先 + 一次，再 - 一次，其余的直接跟题意来。最后把能够到终点的方案除以总方案就是概率。
T5
直接暴力。
我们一次一次看。
首先是第一次它就射中了，概率为 \(\dfrac{a}{b}\)。
然后看第三次如果他射中了，首先要保证第三次以前都没有射中，然后让第三次射中，就是 \(\dfrac{b-a}{b}\times \dfrac{d-c}{d} \times \dfrac{a}{b}\)。
以此类推，只需要保证在第 $2\times n+1 $ 次时，算出来的概率时大于 \(10^{-6}\) 就算可行方案，否则就没有必要在算下去了。（精度）
所以我们可以直接定义一个 \(n=10^6\) 的常数来方便我们实现。
T6
特判烦死了。
显然，要让这个方程有实根，就要保证 \(\Delta\ge 0\)，及 \(p\ge 4\times q\)
我们可以考虑面积法。
先根据样例1来解释一下。
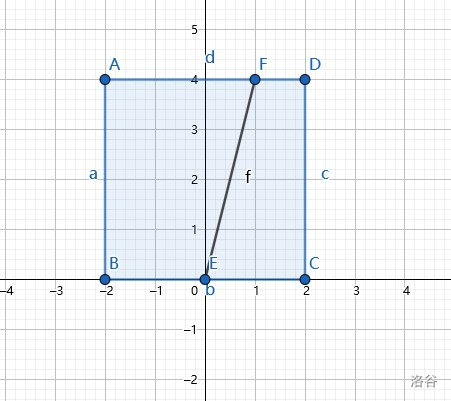
根据上图，对于我们将 \(q\) 看作 \(x\)，\(p\) 看作 \(y\) 建立平面直角坐标系。首先，全集就是整个画出的长方形面积。显然，对于左半部分 \(x<0\) 的，都能满足有实根。然后对于所有在直线 \(y=4x\) 直线及以上部分的区域也都可以保证 \(y\ge 4x\)，及存在实根。
然后我们用存在实根的面积去除以总面积就是概率了。
要注意的就是看 \(y=4x\) 是与长方形的上面交，还是与长方形的侧面交，一边来算面积。
对于 \(a,b=0\) 的情况也需要特判。（比较简单，自己思考答案。）
T7
交了 n 次的 CE 代码。。
首先，我们考虑选出的两张牌中，如果我们选的是同一位置上的，就是 \(\dfrac {1}{n}\) 的概率。然后在考虑选的不同位置上的，首先第二次选时，我们考虑先选任意一个，然后选完这个之后，要选出另一个相同的概率就是从剩下的 \(n\times m-1\) 个数中选出的于其相同的 \(m-1\) 个。
所以总概率就是将两个加起来，也就是 \(\dfrac{1}{n}+\dfrac{n-1}{n}\times \dfrac{m-1}{n\times m -1}\)。
T8
双倍经验。
首先，考虑随机转的概率，能转到没子弹概率显然是序列中 \(0\) 的个数除以总个数。
在考虑直接开枪，由于没有告诉你当前是哪一个档，所以要枚举所有的 0，并记录下一发为 0 的个数。然后用这个数除以序列中 0 的个数，就是直接 shoot 不会有子弹的概率。
最后看两个的大小就可以了。（由于可能存在精度问题，考虑除法改为乘法。）
T9
爆搜水题看半天没看出来。
首先总概率就是将 \(n\) 个中任意选出 \(r\) 个，然后将选出的 \(r\) 个能买东西的概率和没有被选出来的 \(n-r\) 个不能买东西的概率乘起来然后加和。
对于每一个的概率，先算出所有选出的包含它的概率之和再除以总概率就能得到答案。
