FFT简单概述

概念

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

用处

在这里只讨论将adc采集的离散时域信号转换为频率信号的用处
时域：描述数学函数或物理信号对时间的关系。
比如下面这个函数图像，y=0.5sinx+1*cos2x

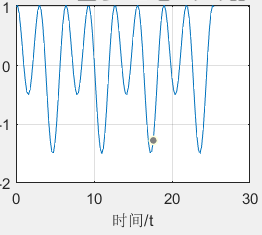
如果描述为电压随着时间的变化，这就是一个时域图
而根据傅里叶变换，任意一个这样的信号我们都可以将其分解为不同频率不同幅值不同相位叠加的正余弦信号的叠加。也就是这样

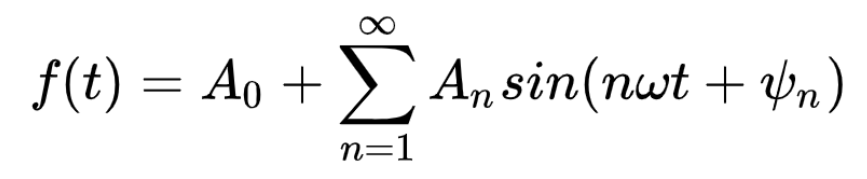
如果我们横坐标为频率，纵坐标为信号的幅值，就可以得到信号的幅频曲线（这里暂时不讨论相位）

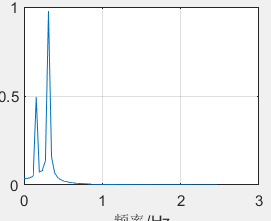
这个图就是上面函数的幅频曲线，我们可以通过表达式看出原本信号由频率为1/pi与1/2pi的正余弦信号构成，且1/pi幅度为1，故幅频曲线中有两个尖峰，且幅值为1:2
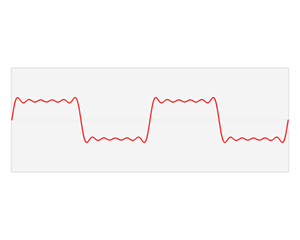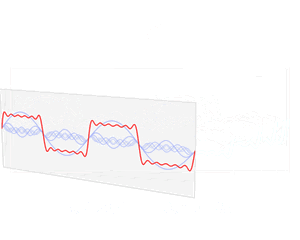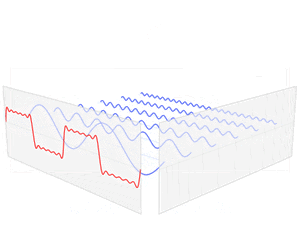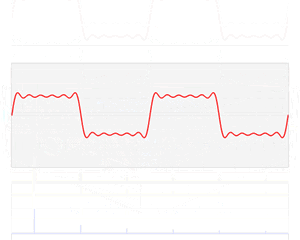
这是一个频率为1/2pi的方波，占空比为50%

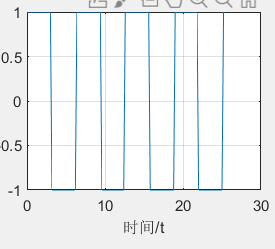
而根据我们上面学习的知识，对它进行傅里叶变换得到的幅频曲线就是这样的

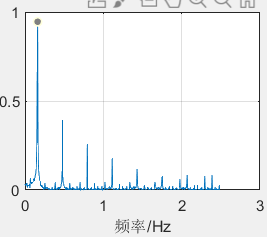
这就是方波的幅频特性，它是由不同相位的奇次谐波构成的
这是wiki上的一个动图，可以根据这个理解一下

在单片机上

这里可以参考https://blog.csdn.net/qq_34022877/article/details/123190943
步骤提供详细，不做赘述