manacher

$\mathrm{manacher}$ 算法可以在线性时间内求出一个串中的最长回文子串。

为了解决偶回文串的中心点非整数，在每个字符之间添加一个字符 #。

为防止越界问题再在串的前后加上奇怪的符号。

记 $mx$ 为当前最长回文串的右端，$id$ 为串中心的位置，$le{n}_{id}$ 为以 $id$ 为中心最多能向右扩展的长度。

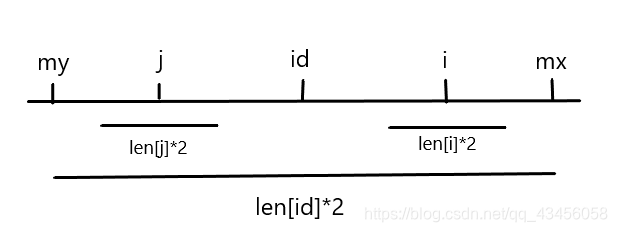
此处 $mx,my$ 与 $i,j$ 关于 $id$ 对称。

• $i\ge mx$，令 $le{n}_i=1$。

• $i<mx$

  • $le{n}_j\le mx-i$

    如上图，此时 $i$ 的最右端还在 $mx$ 内，令 $le{n}_i=le{n}_j$ 即可。

  • $le{n}_j>mx-i$

    

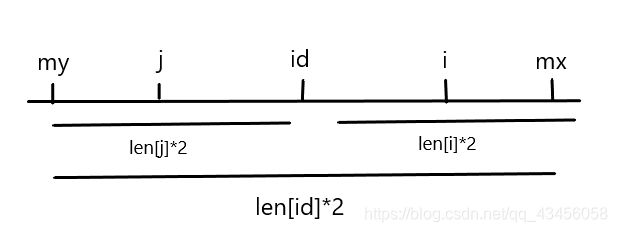
​ 此时 $i$ 超过 $mx$，对 $mx$ 进行更新，将中间点 $id$ 换为 $i$，更新回文串长度。

---

P3805 【模板】manacher

求最长回文串长度。

int n;char t[N],s[N<<1];
int len[N<<1];
void getstr(){
	int m=0;s[m++]='@';
	for(int i=1;i<=n;i++)
		s[m++]='#',s[m++]=t[i];
	s[m++]='#',s[n=m]=0;
}
int manacher(){
	int mx=0,id,mxlen=0;
	for(int i=1;i<n;i++){
		if(mx>i)len[i]=min(mx-i,len[2*id-i]);
		else len[i]=1;
		while(s[i+len[i]]==s[i-len[i]])len[i]++;
		if(len[i]+i>mx){
			mx=len[i]+i,id=i;
			mxlen=max(mxlen,len[i]);
		}
	}
	return mxlen-1;
}
int main(){
	scanf("%s",t+1),n=strlen(t+1);
	getstr();
	printf("%d\n",manacher());
	
	return 0;
}

---

P6216 回文匹配

给出长为 $n$ 的串 $s$ 和长为 $m$ 的串 $t$，问有多少四元组 $(l,r,i,j)$ 满足：

• $1\le l\le i\le j\le r\le n$。

• $s[l:r]$ 是奇回文串。

• $s[i:j]=t$。

答案对 $2^{32}$ 取模。

---

用 $\mathrm{kmp}$ 跑出每对 $(i,j)$，$\mathrm{manacher}$ 跑出所有中心的最长回文串（不需要在中间加特殊字符，因为只要求奇回文串）。

对于 $t$ 在 $s$ 中的每个出现，将其下标的值设为 $1$ 并作前缀和。查询 $t$ 在 $[l,r]$ 中的出现次数即 $su{m}_{r-m+1}-su{m}_{l-1}$。

每个回文串都是区间查，所以作二阶前缀和即可。

record

---

P5446 [THUPC2018] 绿绿和串串

定义 $\mathrm{flip}(S)$ 表示将 $S$ 的长为 $|S|-1$ 的后缀翻转并拼接到 $S$ 后的操作。

对于 $i\in [1,|S|]$，记 $R$ 为前缀 $i$，不断执行 $R\leftarrow \mathrm{flip}(R)$，问 $S$ 是否为 $R$ 的前缀。输出这些 $i$。

多测。$|S|\le {10}^6$，$\sum |S|\le 5\times {10}^6$。

---

特判 $|R|=|S|$ 的情况，那么 $\mathrm{flip}(R)$ 一定为奇回文串。

跑 $\mathrm{manacher}$ 后暴力判回文长度即可。特别地，当 $|\mathrm{flip}(R)|\ge |S|$ 时特判。

时间复杂度 $O(n\log n)$。

record

---

P9606 [CERC2019] ABB

问在串末尾添加若干字符使其成为回文串的最小数量。

---

对于中心点 $i$，若最长回文子串到达串尾，更新答案即可。

record

---