黄金点第三次博客

上周回顾：经过结对编程的实际体验以及目前掌握的知识来看，我们将加入 AI 预测（玩家作弊）功能以及多轮结果可视化作为项目后续的方向。下面是针对后续发展方向的相关分析与测试：

一. 可视化部分

　　1. 实现思路及模块框架

　　我们小组希望通过可视化模块对所有玩家在游戏进行中以及游戏结束后展示每位玩家的历史选择（0 ~ 100 整数）、历史得分情况（每局游戏只有一位赢家会得到 N 分，其中 N 为当前玩家的总数；只有一位输家会扣除 -2 分）、最后总分情况、每局游戏的黄金点变化情况。针对以上需求，我们计划采用 java 调用 MySQL 数据库并在前端渲染的思路，在游戏结束后玩家可以选择查看。

　2. 效果示例图

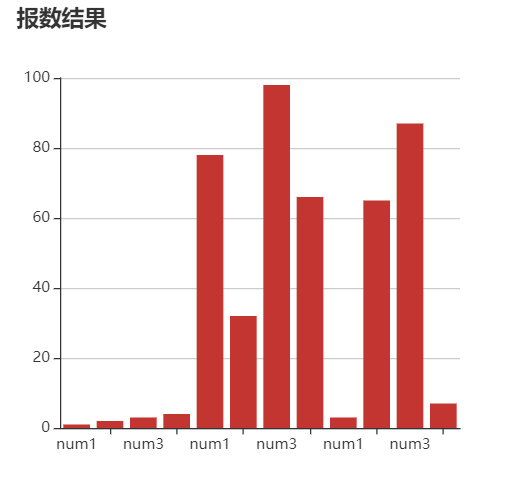
　　　　2.1 玩家历史选择情况

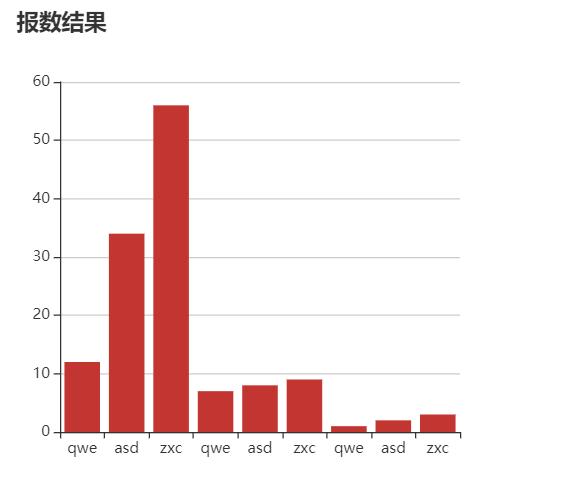
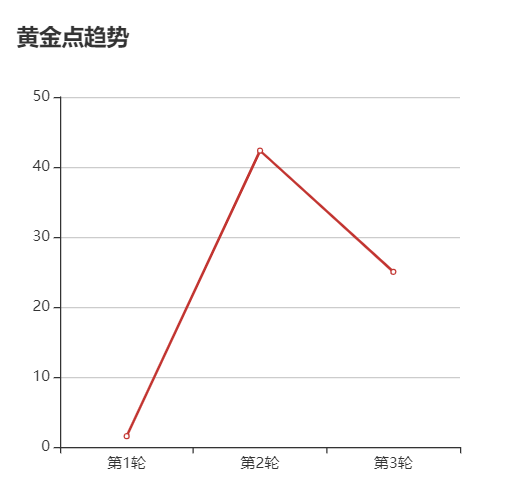
　　　　2.2 黄金点历史趋势折线图

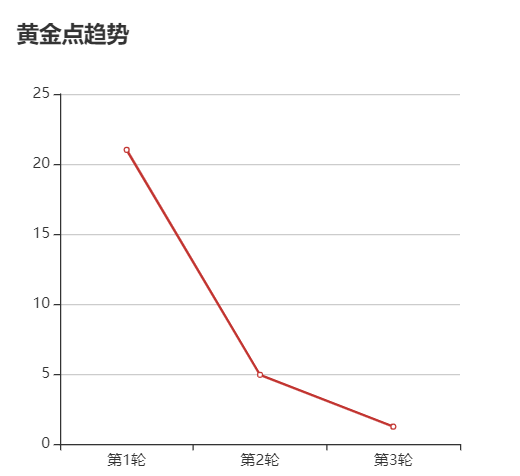
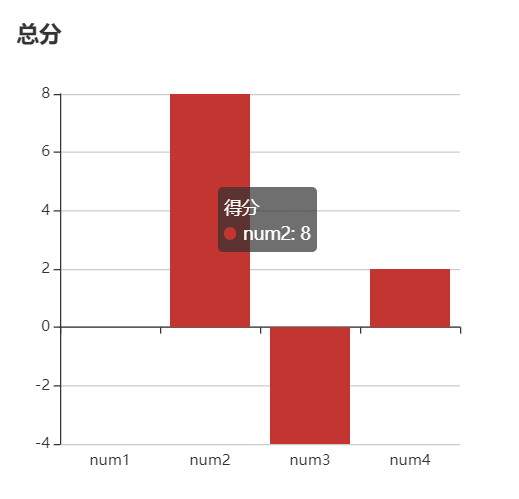
　　　　2.3 玩家总分瀑布图

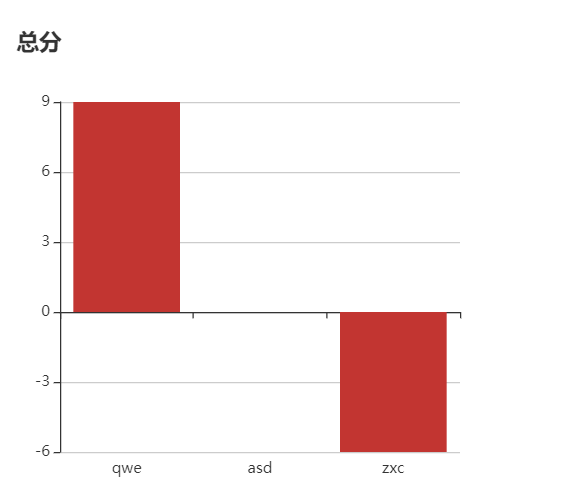
　　3. 一个完整游戏过程（带可视化结果图）

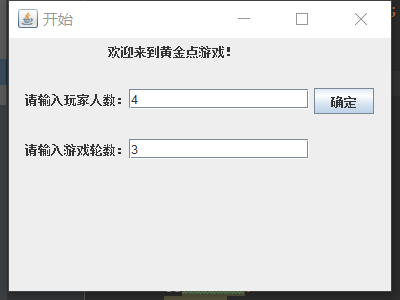
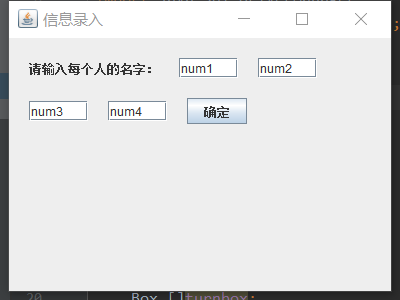
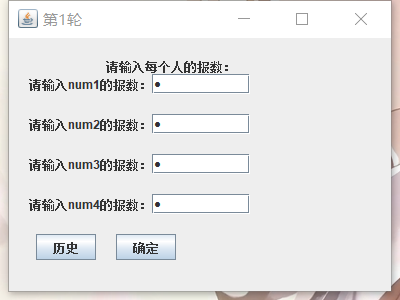
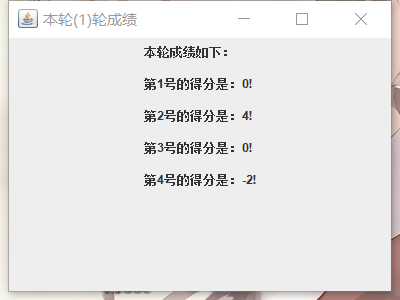
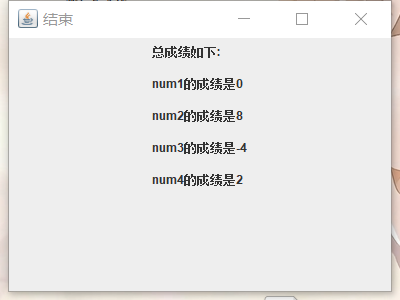
　　4. 代码实现

　　　　4.1 html 前端渲染

  1 <!DOCTYPE html>
  2 <html lang="en">
  3 <head>
  4     <meta charset="UTF-8">
  5     <title>统计</title>
  6     <script src="jquery-2.1.4.min.js" type="text/javascript"></script>
  7     <style>
  8     </style>
  9     
 10 </head>
 11 <body>
 12 <div id="d1" style="height: 400px;width:400px"></div>
 13 <div id="d2" style="height: 400px;width:400px"></div>
 14 <div id="d3" style="height: 400px;width:400px"></div>
 15 <script src="echarts.min.js"></script>
 16 <script src="jquery-2.1.4.min.js" type="text/javascript"></script>
 17 <script>
 18     var option1={
 19         title:{
 20             text:"报数结果"
 21         },
 22         tooltip:{},
 23         lengend:{
 24             data:[]
 25         },
 26         xAxis:{
 27             data:[]
 28         },
 29         yAxis:{
 30             type:'value'
 31         },
 32         series:[
 33             {
 34                 name:"报数",
 35                 type:"bar",
 36                 data:[]
 37             }
 38         ]
 39     };
 40 
 41     var option2={
 42         title:{
 43             text:"黄金点趋势"
 44         },
 45         tooltip:{},
 46         lengend:{
 47             data:[]
 48         },
 49         xAxis:{
 50             data:[]
 51         },
 52         yAxis:{
 53             type:'value'
 54         },
 55         series:[
 56             {
 57                 name:"黄金点",
 58                 type:"line",
 59                 data:[]
 60             }
 61         ]
 62     };
 63 
 64     var option3={
 65         title:{
 66             text:"总分"
 67         },
 68         tooltip:{},
 69         lengend:{
 70             data:[]
 71         },
 72         xAxis:{
 73             data:[]
 74         },
 75         yAxis:{
 76             type:'value'
 77         },
 78         series:[
 79             {
 80                 name:"得分",
 81                 type:"bar",
 82                 data:[]
 83             }
 84         ]
 85     };
 86 
 87     var myChart1 = echarts.init(document.getElementById('d1'));
 88     var myChart2 = echarts.init(document.getElementById('d2'));
 89     var myChart3 = echarts.init(document.getElementById('d3'));
 90 
 91 
 92     function drawEcharts1() {
 93         var url="all";
 94         $.post(url,function (result) {
 95             for(var i=0;i<result.length;i++){
 96                 option1.xAxis.data.push(result[i].name);
 97             }
 98             for(var i=0;i<result.length;i++){
 99                 option1.series[0].data.push(result[i].num);
100             }
101             myChart1.setOption(option1);
102         })
103     }
104     drawEcharts1();
105     function drawEcharts2() {
106         var url="gold";
107         $.post(url,function (result) {
108             for(var i=0;i<result.length;i++){
109                 option2.xAxis.data.push("第"+(i+1)+"轮");
110             }
111             for(var i=0;i<result.length;i++){
112                 option2.series[0].data.push(result[i].gold);
113             }
114             myChart2.setOption(option2);
115         })
116     }
117     drawEcharts2()
118 
119     function drawEcharts3() {
120         var url="score";
121         $.post(url,function (result) {
122             for(var i=0;i<result.length;i++){
123                 option3.xAxis.data.push(result[i].name);
124             }
125             for(var i=0;i<result.length;i++){
126                 option3.series[0].data.push(result[i].score);
127             }
128             myChart3.setOption(option3);
129         })
130     }
131     drawEcharts3()
132     function del() {
133         url="del";
134         $.post(url)
135     }
136 </script>
137 <button onclick="del()">清除缓存</button>
138 </body>
139 
140 </html>

　　　　4.2 MySQL 后端调用

 1 package com.example.demo.lzl.Controller;
 2 
 3 
 4 import javafx.beans.binding.IntegerBinding;
 5 import org.springframework.beans.factory.annotation.Autowired;
 6 import org.springframework.jdbc.core.JdbcTemplate;
 7 import org.springframework.web.bind.annotation.CrossOrigin;
 8 import org.springframework.web.bind.annotation.RequestMapping;
 9 import org.springframework.web.bind.annotation.ResponseBody;
10 import org.springframework.web.bind.annotation.RestController;
11 
12 import java.util.ArrayList;
13 import java.util.HashMap;
14 import java.util.List;
15 import java.util.Map;
16 
17 @RestController
18 public class FormController {
19     @Autowired
20     private JdbcTemplate jdbcTemplate;
21 
22     @CrossOrigin
23     @RequestMapping("/all")
24     @ResponseBody
25     public List<Map<String,Object>> all(){
26         String sql1="select * from gold_point";
27         List<Map<String,Object>>list=jdbcTemplate.queryForList(sql1);
28         System.out.println(list);
29         return list;
30     }
31 
32     @CrossOrigin
33     @RequestMapping("/gold")
34     @ResponseBody
35     public List<Map<String,Object>> gold(){
36         String sql1="select * from gold_point";
37         List<Map<String,Object>>list=jdbcTemplate.queryForList(sql1);
38         String name=(String) list.get(0).get("name");
39         String sql2="select * from gold_point where name=?";
40         Object args[]={name};
41         List<Map<String,Object>>list2=jdbcTemplate.queryForList(sql2,args);
42         return list2;
43     }
44 
45     @CrossOrigin
46     @RequestMapping("/score")
47     @ResponseBody
48     public List<Map<String,Object>> score(){
49         String sql1="select * from gold_point where turn=1";//取得第一轮所有数据
50         List<Map<String,Object>>list1=jdbcTemplate.queryForList(sql1);
51         List<String>list2=new ArrayList<>();//用来存储所有名字
52         for (int i=0;i<list1.size();i++){
53             list2.add((String) list1.get(i).get("name"));
54         }
55         List<Map<String,Object>>list3=new ArrayList<>();//记录每个人的总分
56         for (int j=0;j<list2.size();j++){//查询每个人
57             String sql2="select * from gold_point where name=?";
58             Object args2[]={list2.get(j)};
59             List<Map<String,Object>>list4=jdbcTemplate.queryForList(sql2,args2);//存储一个人的所有记录
60             Map<String,Object>map=new HashMap<String,Object>();
61             map.put("name",list4.get(0).get("name"));
62             map.put("score",list4.get(0).get("score"));
63             for (int k=1;k<list4.size();k++){
64                 map.replace("score",(Integer)map.get("score")+(Integer)list4.get(k).get("score"));
65             }
66             list3.add(map);
67         }
68         System.out.println(list3);
69         return list3;
70     }
71     @CrossOrigin
72     @RequestMapping("/del")
73     @ResponseBody
74     public void del(){
75         String sql="delete from gold_point";
76         jdbcTemplate.update(sql);
77     }
78 }

　　在 MySQL 后端调用时，我们利用 java util 类中的 Map 哈希表查找算法，一个属性对应一个键值，这样可以实现 O(1) 的时间复杂度，相比传统的 list 和 vector 容器有效提高了查找速率，使前端能更快地渲染出可视化模块的图形。

二. AI 部分初见

　　1. 初步猜想及验证

　　在这一部分中，我们预计体现 “AI” 的思路是：在第一局结束后的每一局中，每位玩家都会总共有三次 “作弊”机会，如果选择作弊，那么系统将会根据算法给出可能在后续游戏中获得更高分数的当前选择。　

　　结合游戏规则我们发现，每一轮玩家所确定的黄金点都会乘上0.618，那么这个值是否会越来越小呢，以至于最终趋近于 0 呢？我们设想“聪明的”玩家会这样想：第一轮根据正态分布规律，最后的黄金点很有可能在 (0 + 100) / 2 * 0.618 = 30.9 附近；第二轮如果大家都想赢，那么以上一轮的黄金点作为这一轮大家的平均数，玩家就可能会选择上一轮黄金点的0.618倍附近的数作为这一轮自己的输入;...我们选择 “附近”的范围为 +-5。我们小组用计算算计模拟出了这一过程，想观察黄金点分布的规律。

　　我们假设玩家人数是在 0-100 中的随机数，游戏的总局数也是 0-100 中的随机数，我们按照上述规则模拟了十次：（这里仅展示每次模拟的前20局游戏）

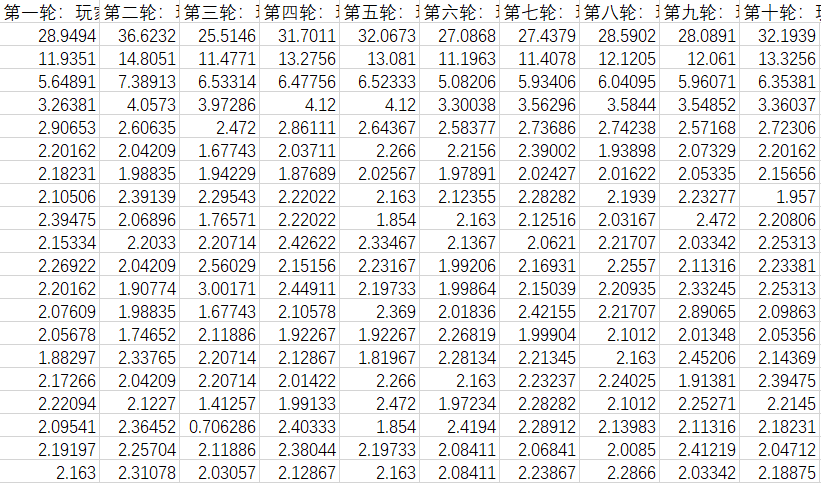
　　我们的模拟的人数与局数数据如下：

模拟次数	随机玩家人数	随机游戏局数
第一次	64	54
第二次	23	98
第三次	7	81
第四次	27	70
第五次	18	50
第六次	94	86
第七次	98	69
第八次	80	61
第九次	31	64
第十次	96	39

　　在如此大的样本下，我们得出了黄金点的分布曲线：

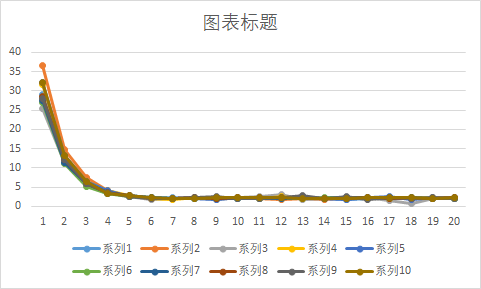
　　（1）十次模拟中的前20局曲线黄金点分布图：

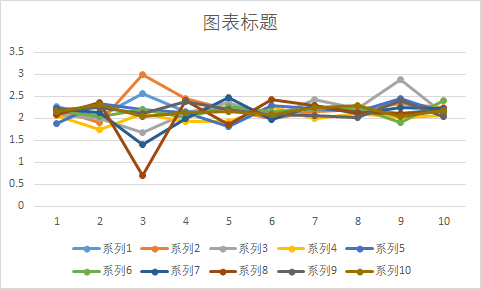
　　（2）十次模拟中每次的第 11-20 局黄金点分布图：

　　代码如下：

 1 for(now_round_num = 1; now_round_num <= round_num; now_round_num++){
 2             double now_round_sum = 0;
 3             if(now_round_num == 1){
 4                 now_round_sum = 0;
 5                 for(int i = 0; i < player_num; i++){
 6                     double temp_rand_num = 0;
 7                     while(temp_rand_num == 0)    temp_rand_num = rand() % 100;  // 随机数范围为[0, 100)，如果得到0则重新产生随机数直到不为0 
 8                     point_choice[i] = temp_rand_num;
 9                     now_round_sum += point_choice[i];
10                 }
11                 double gold_result = (now_round_sum / player_num) * gold_point;
12                 history_GoldPoint.push_back(gold_result);
13                 now_round_sum = 0;
14                 continue;
15             }
16             now_round_sum = 0;
17             int Size = history_GoldPoint.size();
18             double predict_num = history_GoldPoint[Size - 1] * gold_point;
19             for(int i = 0; i < player_num; i++){
20                 int type = rand() % 1;
21                 if(type == 0)    point_choice[i] = (predict_num + rand() % 6);
22                 else if(type == 1){
23                     if(predict_num > rand() % 6)    point_choice[i] = predict_num - rand() % 6;
24                     else    point_choice[i] = predict_num + rand() % 6; 
25                 } 
26                 now_round_sum += point_choice[i];
27             }
28             double gold_result = (now_round_sum / player_num) * gold_point;
29             history_GoldPoint.push_back(gold_result);
30             now_round_sum = 0;
31             
32         }

　　观察发现，在条件 ①每位玩家每局仅输入一个数据，不存在干扰；②只以上一局的黄金点作为当前局的参考的情况下，黄金点最后并没有降至 0（因为要求输入恒大于0），1-5 局迅速减小，之后在 0.5-3 单位内波动。

　　我们发现，如果只是这样单纯地以上一局黄金点作为参考，比较简单，受随机扰动的可能较大。特别是在玩家的输入每次变成了2后，其局限性更为显著。经查阅资料后，我们打算使用强化学习中的 Q-Learning算法，描述出当前预测的所有状态，取奖励得分最高的状态作为给出预测黄金点的依据。

　　2. 强化学习及Q-Learning 算法简介

　　强化学习和遗传算法优胜劣汰的思想类似，通过奖惩机制不断强化好的行为（action），弱化坏的行为。至于什么是好的行为，什么是坏的行为，跟你要解决的具体问题有关，比如路径规划问题，走距离目标点较近的路线就是好的行为，走距离目标点较远的路线就是坏的行为。

　　强化学习包含四要素：agent、环境状态、动作和奖励，目标是获得最多的累计奖励。

　　Q learning 融合了马尔科夫过程和动态规划，使用贝尔曼方程求解马尔科夫过程。今天我们不展开讲马尔科夫过程和贝尔曼方程，因为那样入门起来就不简单了，今天仅从算法过程的角度理解并入门，马尔科夫过程和贝尔曼方程是入门后再去深入研究的原理性部分。

　　Q learning 最重要的数据结构为 Q 表，Q 是 quality 的缩写。算法最终就是要学习到一张好的 Q 表，这样我们就可以根据 Q 表对环境中的任何情况（状态）都能给出一个好的反应（动作）。具体的，就是每次都选择 Q 表中对应状态下具有最大 Q 值的动作。

　　Q 表一般用二维数组表示，每一行表示一个状态，每一列表示一个动作。参考已有的资料，我们将黄金点游戏在 Q 表中设置为共有7个动作：

Action	Number
0	前一轮黄金点（从第二局开始）
1	前两轮黄金点的均值（如果有的话）
2	前三轮黄金点的均值（如果有的话）
3	前十轮中每隔1轮进行采样后的GN的均值
4	前十轮中每隔2轮进行采样后的GN的均值
5	前十轮中最大的三个的GN的均值
6	前十轮中最小的三个的GN的均值

　　算法流程图如下：

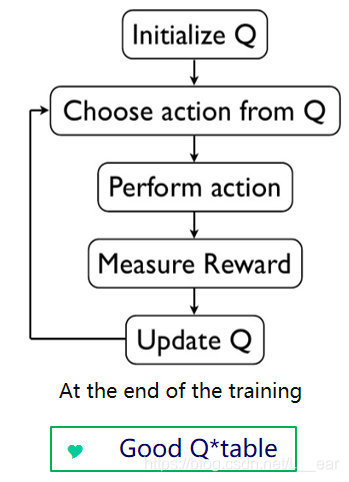
　　用伪代码可以这样表示：

1 初始化Q表
2 while Q表未收敛:
3     初始化状态s，开始新一轮训练
4     while s != 目标状态
5         使用策略（E-greedy）获得动作a
6         执行动作转换到下一个状态s1，并获得奖励r(s,a)
7         Q[s,a] = (1-alpha)*Q[s,a]+alpha*(r(s,a)+gamma*max(Q[s1])) // update Q
8         s = s1

　　其中，关于 Q 表的更新公式为：

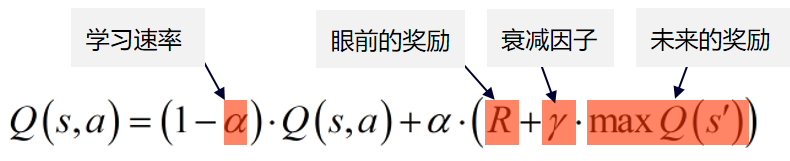
　　眼前的奖励定义为：参照马尔科夫过程，当前状态值的变化仅与上一次状态有关，这里一共有7个 action，那么如果先初始化 R（奖励）表：
　　

R = {
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
　　[0, 0, 0, 0, 0, 0, 0];
}

　　初始，每一个状态做出的每一个 action 得到的奖励都是零。如果我们定义上一个状态的结果是 _R, 那么当前动作（选择的分数）离上一次黄金点最远的奖励设为玩家人数 N ，离上一次黄金点距离最近的奖励设置为 -2, 其他奖励为 0（不得分）。

　　目前，这一部分仍在开发过程中。

[0, 0, 0, 0, 0, 0, 0];

posted @ 2020-11-15 22:32 软工课设第29组阅读(95) 评论(0) 收藏举报

刷新页面返回顶部

软工课设第29组-软工课设黄金点项目