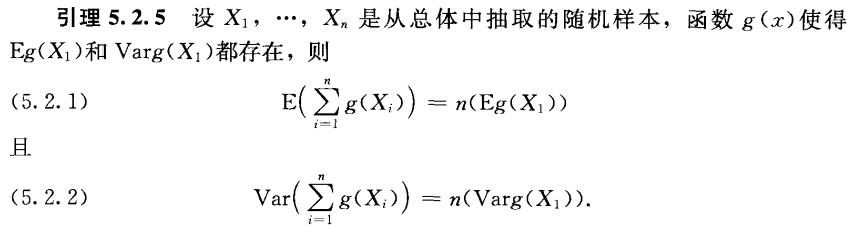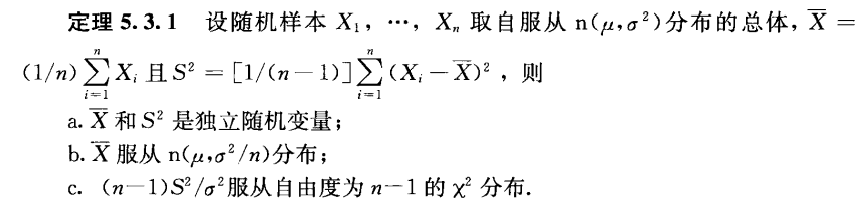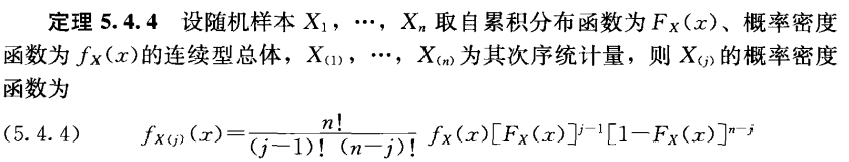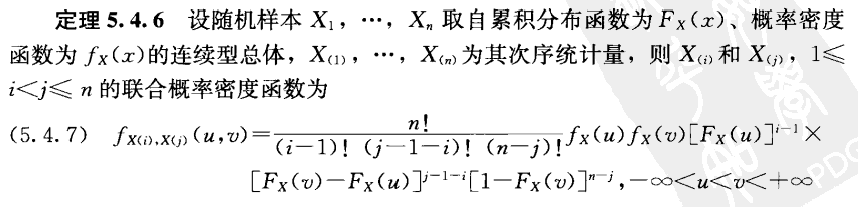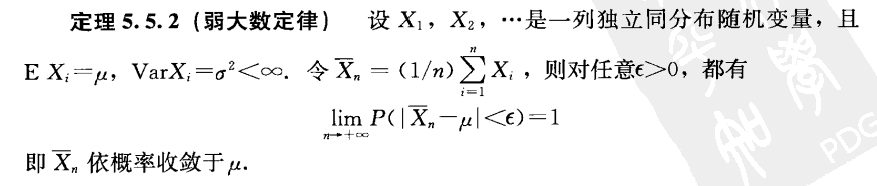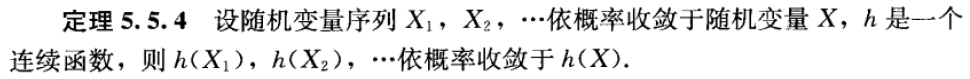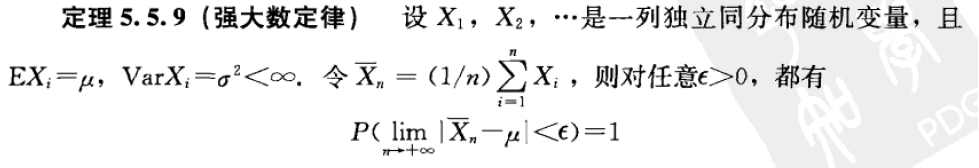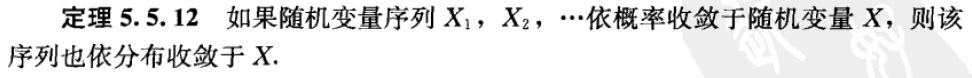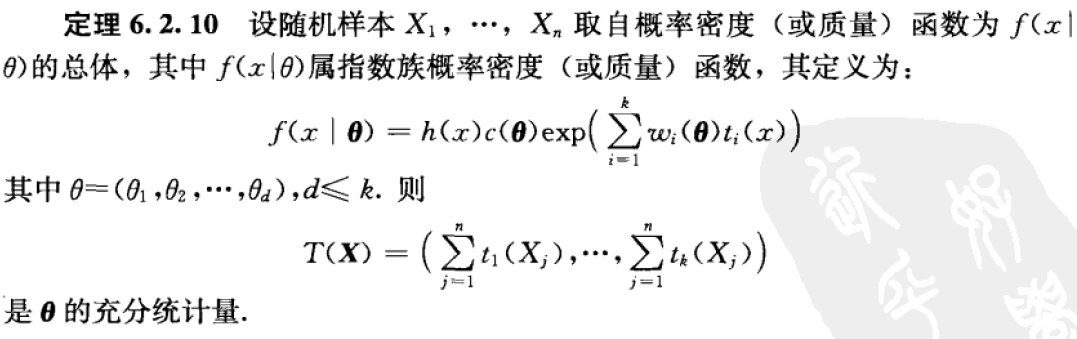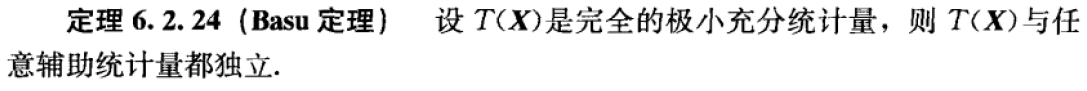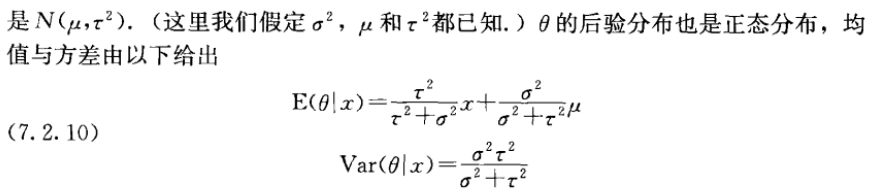统计推断 复习笔记
期末速成 Day 2/2
目录
Ch1 概率论
Ch2 变换和期望
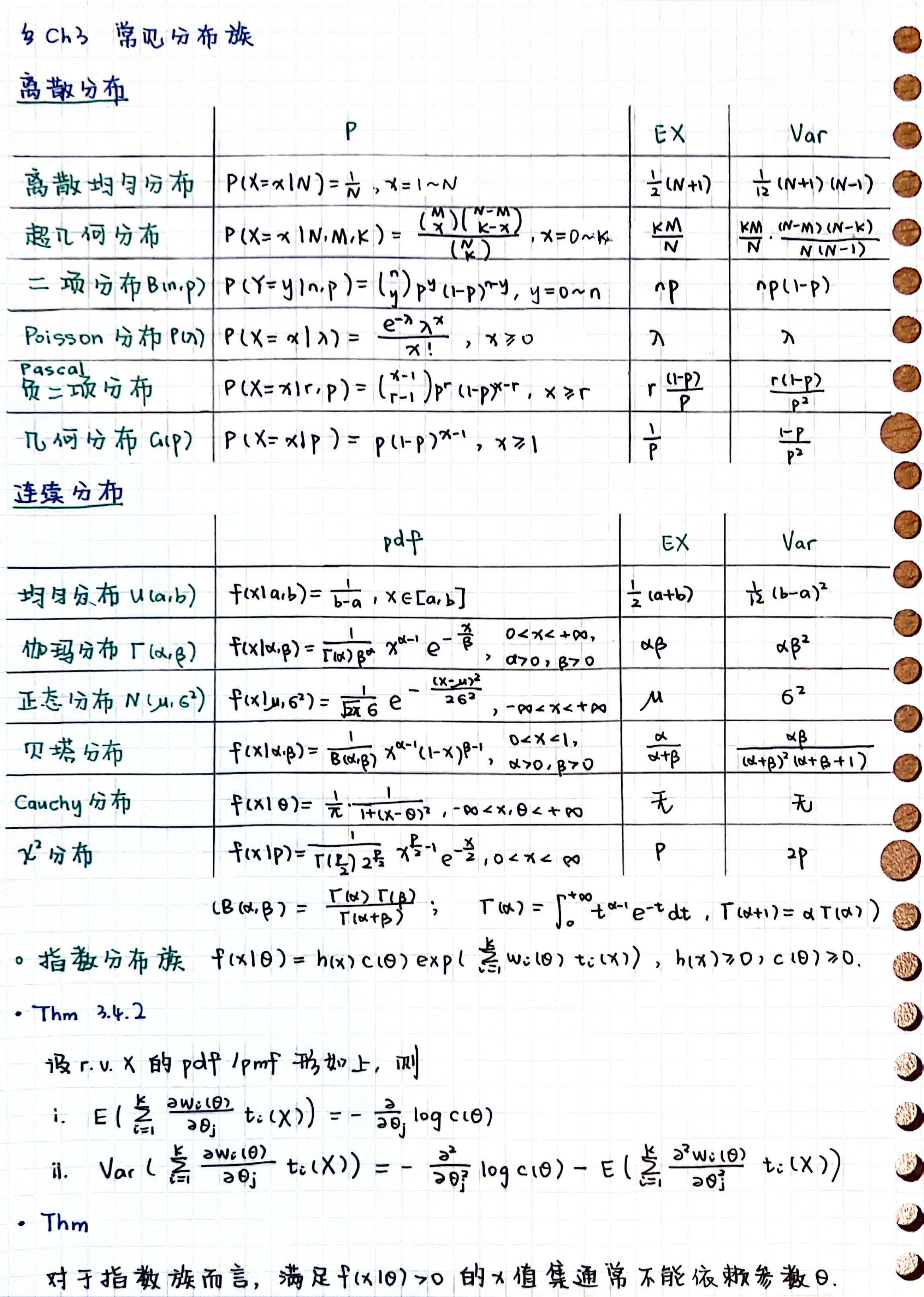
Ch3 常见分布族
Ch4 多维随机变量
Thm 4.6.11（多个随机向量独立）
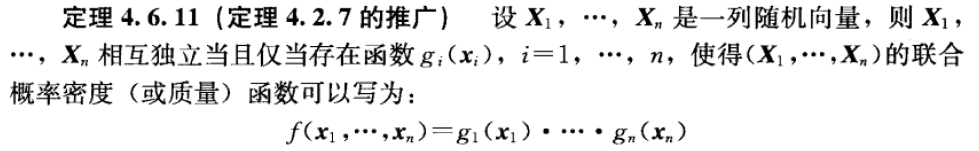
Thm 4.6.12（多个随机向量独立 \(\Rightarrow\) 一元函数独立）
Ch5 随机样本的性质
5.1 随机样本的基本概念
Def
- 随机样本
- 总体：\(x\sim f(x)\)
5.2 随机样本中随机变量的和
Def
- 统计量：\(Y=T(x_1,...,x_n)\)（不能是含参数的函数）
- 抽样分布：\(Y\) 的概率分布
- 样本均值：随机样本值的算术平均
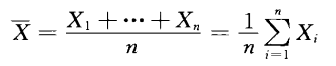
- 样本方差：
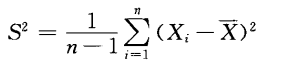，样本标准差 \(S\)
Theorem 5.2.4
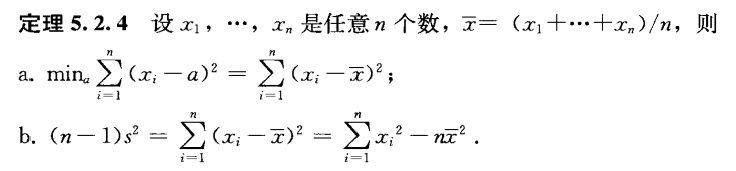
- \(min_a\Sigma_{i=1}^n|x_i-a|=\Sigma_{i=1}^n|x_i-median(x_1,...,x_n)|\)
Lemma 5.2.5
Theorem 5.2.6（\(\overline X\) 和 \(S^2\) 的无偏性）
- 统计量 \(\overline X\) 和 \(S^2\) 分别称为 \(\mu\) 和 \(\sigma^2\) 的无偏估计量
Example 5.2.10（Cauchy 随机变量的和）
- \(Cauchy(0,\sigma)+Cauchy(0,\tau)\sim Cauchy(0,\sigma+\tau)\)
5.3 正态分布的抽样
Theorem 5.3.1（正态分布下 \(\overline X\) 和 \(S^2\) 的分布）
Lemma 5.3.2（关于 \(\chi^2\) 随机变量的若干事实）
正态随机变量的线性组合
Lemma 5.3.3
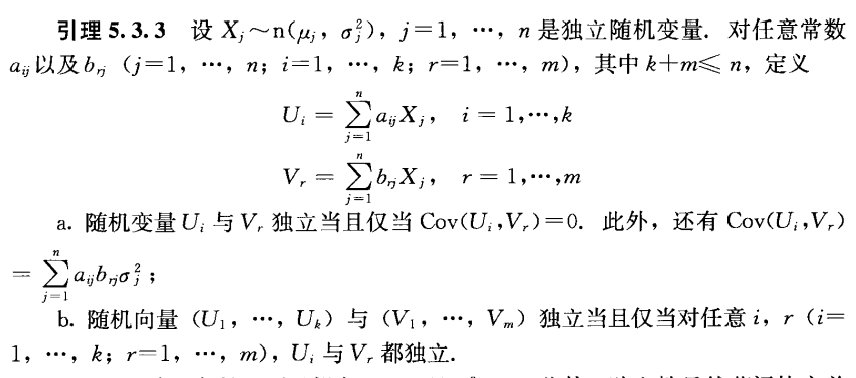
- 对于由独立的正态随机变量的线性函数构成的随机变量，协方差等于 0 等价于独立。
导出分布：\(t\) 分布与 \(F\) 分布
略。
5.4 次序统计量
Def
- 次序统计量：\(X_{(1)},...,X_{(n)}\)
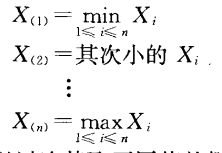
- 样本极差 \(R=X_{(n)}-X_{(1)}\)
- 样本中程数 midrange \(M=\frac{1}{2}(X_{(1)}+X_{(n)})\)
Theorem 5.4.4（次序统计量的 pdf）
Example 5.4.5
Theorem 5.4.6（次序统计量的联合 pdf）
5.5 收敛的概念
依概率收敛
Def
- 依概率收敛：
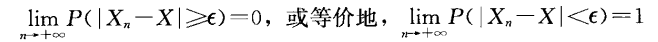
Theorem 5.5.2（弱大数定律：样本均值依概率收敛于总体均值）
Example 5.5.3（\(S^2\) 的相合性：\(lim_{n\rightarrow +\infty}VarS_n^2=0 \Rightarrow S_n^2\) 依概率收敛于 \(\sigma^2\)）
Thm 5.5.4（依概率收敛 \(\Rightarrow\) 连续函数依概率收敛）
几乎处处收敛
Def
- 几乎处处收敛：
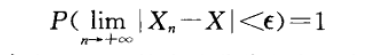（几乎处处收敛 \(\Rightarrow\) 依概率收敛）
Theorem 5.5.9（强大数定律：样本均值几乎处处收敛于整体均值）
依分布收敛
Def
- 依分布收敛：
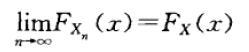
Theorem 5.5.12（依概率收敛于随机变量 \(\Rightarrow\) 依分布收敛）
Theorem 5.5.13（依概率收敛于常数 \(\Leftrightarrow\) 依分布收敛）
Theorem 5.5.15（中心极限定理：总体分布方差有限 \(\Rightarrow \sqrt n (\overline{X_n}-\mu)/\sigma\) 依概率收敛于 \(N(0,1)\)）
- 可以用于近似计算概率
Theorem 5.5.17（Slutsky 定理）
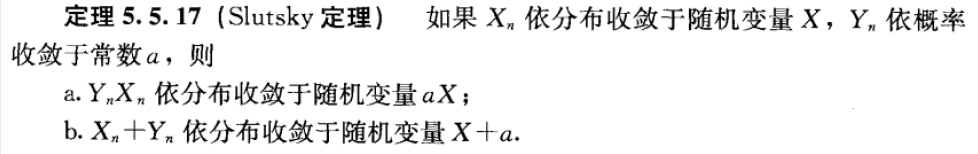
- c. \(\frac{X_n}{Y_n}\rightarrow \frac{X}{C}\)
\(\triangle\) 方法
Theorem 5.5.24（\(\triangle\) 方法）
Theorem 5.5.26（二阶 \(\triangle\) 方法）
5.6 生成随机样本
直接法
间接法
舍选法
Ch6 数据简化原理
6.2 充分性原理
充分统计量
Def
- 充分统计量：如果样本 \(X\) 在已知统计量 \(T(X)\) 取值时的条件分布 \(P\{X=x|T(X)=T(x)\}\) 与 \(\theta\) 无关，则称 \(T(X)\) 为充分统计量。
- 除指数族分布外，其它分布中少有维数低于样本大小的充分统计量，因此很多时候次序统计量已经是我们能找到的最好的充分统计量。
Theorem 6.2.6（因子分解定理）
Theorem 6.2.10（指数族总体的充分统计量）
极小充分统计量
Def
- 极小充分统计量：称充分统计量 \(T(X)\) 是极小充分统计量，如果对其余任一充分统计量 \(T'(X)\)，\(T(X)\) 都是 \(T'(X)\) 的函数。
Theorem 6.2.13（Lehman and Scheffe）
辅助统计量
Def
- 辅助统计量：如果统计量 \(S(X)\) 的分布与 \(\theta\) 无关，则称它为辅助统计量。
Example 6.2.18-19（位置族、尺度族辅助统计量）
完全统计量
Def
- 完全的概率分布族：设 \(f(x|\theta),\theta \in \Theta\)，\(\{ P_\theta|\theta \in \Theta\}\) 是概率分布族，称 \(\{ P_\theta|\theta \in \Theta\}\) 是完全的，如果对 \(X\sim P_\theta\)，若 \(E_\theta g(X)=\int g(x) dP_\theta(x)=0,\forall\theta\in\Theta\)，则有 \(g(x)=0,a.e.\)
- 完全统计量：
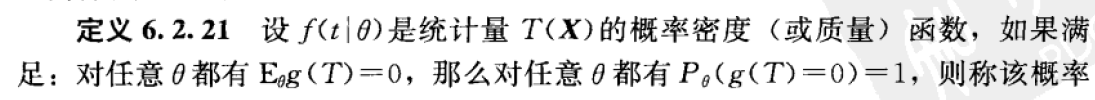
Theorem 6.2.24（Basu 定理：极小充分统计量和任意辅助统计量独立的条件）
Theorem 6.2.25（指数族总体的完全统计量）
Ch7 点估计
7.2 求估计量的方法
Def
- 点估计量：样本的任何一个函数 \(W(X_1,...,X_n)\)
Theorem（统计学基本定理）
- \(X_1,...,X_n\stackrel{i.i.d.}{\sim} F(x)\)，经验分布函数 \(F_n(x)=\frac{1}{n}\Sigma^n_{i=1}I(x_i≤x)\)，则有 \(F_n(x)\stackrel{a.s.}{\rightarrow} F(x),\ \forall x\)
Def（矩估计）
- 由统计学基本定理，若 \(|Eg(X)|<\infty\)，可以取 \(\frac{1}{n}\Sigma_{i=1}^n g(x_i) \rightarrow Eg(x)=G(\theta)\) 作为 \(\theta\) 的估计。当取 \(g(x)=x^k\) 时，\(G_k(\theta)=E_\theta x^k:=\frac{1}{n}\Sigma_{i=1}^n x_i^k\) 称为 \(\theta\) 的矩估计。
最大似然估计
Def
- 似然函数：若 \(X_1,...,X_n\stackrel{i.i.d.}{\sim} f(x|\theta),\ \theta \in \Theta\)，则 \(L(\theta|x_1,...,x_n)=\Pi^n_{i=1}f(x_i|\theta)\) 称为似然函数。
- 最大似然估计 MLE：
- 计算方法：算 \(L(\theta)\)，求一阶导的零点，再求二阶导证明最大。
Theorem 7.2.10（最大似然估计的不变原理）
Bayes 估计
Def
- 先验分布：在见到抽样数据之前，通过预先对 \(\theta\) 了解的信息，假设 \(\theta\sim \pi(\theta)\)
- 后验分布：给定样本 \(x\) 的条件下 \(\theta\) 的条件分布，即 \(\pi(\theta|x)=\frac{f(x|\theta)\pi(\theta)}{m(x)}\)，其中 \(m(x)\) 为 \(x\) 的边缘分布，\(m(x)=\int f(x|\theta)\pi(\theta)d\theta\)
- 可以利用后验分布 \(\pi(\theta|x)\) 对 \(\theta\) 进行推断，比如取后验均值 \(\underset{\pi(\theta|x)}{E}\ \theta\)，最大值 \(\underset{\theta}{max}\ \pi(\theta|x)\) 作为 \(\theta\) 的估计。
Example 7.2.14（二项分布的 Bayes 估计）
- 设 \(X_1,...,X_n\stackrel{i.i.d.}{\sim} Bernoulli(p)\)，则 \(Y=\Sigma_{i=1}^n X_i\sim binomial(n,p)\)。假设 \(p\) 的先验分布是 Beta 分布，\(p\sim beta(\alpha,\beta)\)，则后验分布 \(f(p|y)\sim beta(y+\alpha,n-y+\beta)\)，用后验分布的均值估计 \(p\)，得 \(\widehat p_B=\frac{y+\alpha}{\alpha+\beta+n}=(\frac{n}{\alpha+\beta+n})(\frac{y}{n})+(\frac{\alpha+\beta}{\alpha+\beta+n})(\frac{\alpha}{\alpha+\beta})\)，为样本均值 \(\frac{y}{n}\) 和先验均值 \(\frac{\alpha}{\alpha+\beta}\) 的一个线性组合。
Example 7.2.16（正态分布的 Bayes 估计）
7.3 估计量的评价方法
Def
- 相合性：当 \(n\rightarrow +\infty\) 时，若 \(\widehat\theta_n \stackrel{P}{\rightarrow} \theta,\ \theta\in\Theta\)，则称 \(\widehat\theta_n\) 是 \(\theta\) 的（弱）相合估计。
均方误差
Def
- 均方误差 MSE：参数 \(\theta\) 的估计量 \(\widehat\theta_n\) 的均方误差定义为 \(E|\widehat\theta_n-\theta|^2=Var(\widehat\theta_n)+(E\widehat\theta_n-\theta)^2\)
- 偏倚 bias：\(Bias(\widehat\theta_n)=E\widehat\theta_n-\theta\)
- 无偏估计量：满足 \(Bias(\widehat\theta_n)=0\)，即 \(E|\widehat\theta_n-\theta|^2=Var(\widehat\theta_n)\)
UMVUE
Def
- 一致最小方差无偏估计量 UMVUE：
Theorem 7.3.9（Cramer-Rao不等式：估计量方差下界）
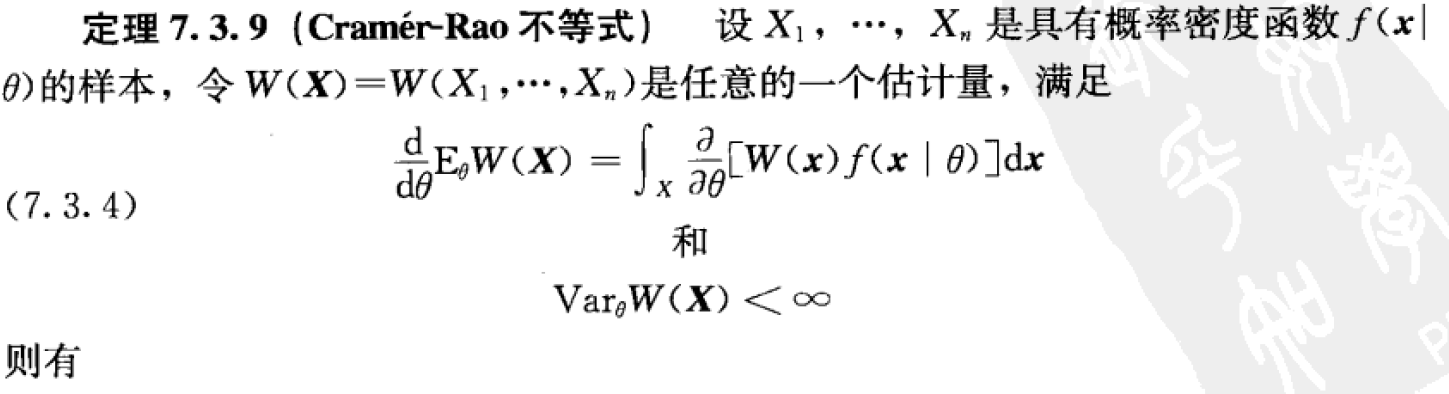
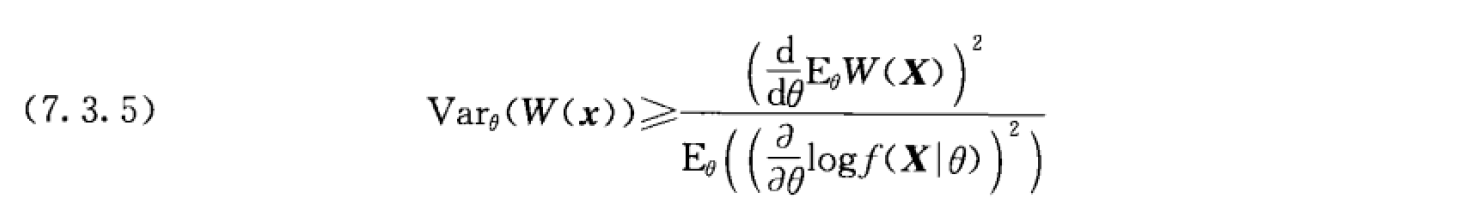
- 取 \(W(X)\) 为 \(\tau(\theta)\) 的无偏估计，则 \(E_\theta W(X)=\tau(\theta)\)。上式等号成立当且仅当存在 \(c(\theta),d(\theta)\)，使得 \(W(X)-\tau(\theta)=d(\theta)(\frac{\partial}{\partial \theta}\log f(x|\theta))\)
- 一般来说，若概率密度函数 \(f(x|\theta)\) 不等于零的范围（支撑集）依赖于参数，该定理将不再适用。
- Fisher 信息量 \(I(\theta)=E_\theta ((\frac{\partial}{\partial \theta}\log f(x|\theta))^2)\)
UMVUE 与充分统计量
Lemma
Theorem 7.3.17（Rao-Blackwell：利用充分统计量获得更好的无偏估计）
Theorem 7.3.19（UMVUE 的唯一性）
- 证明思路：Cauchy-Schwarz 不等式
Theorem 7.3.20
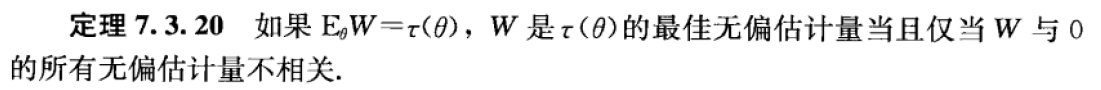
- 即：若 \(W\) 是 UMVUE，那么 \(Cov_\theta(W,U)=0,\ \forall\theta,\ \forall U\) 满足 \(E_\theta U=0\)
Theorem 7.3.23
- 设 \(X_1,...,X_n\stackrel{i.i.d.}{\sim} f(x|\theta),\ \theta\in\Theta\)，\(W(x)\) 为 \(\tau(\theta)\) 的一个无偏估计，\(T(x)\) 是一个充分完全统计量，则 \(E(W|T)\) 是 \(\tau(\theta)\) 的 UMVUE。
Ch8 假设检验
Def
- 假设：关于总体参数的一个陈述。
- 原假设 \(H_0\)，备择假设 \(H_1\)：一个假设检验问题中两个互补的假设，一般格式是 \(H_0:\theta\in\Theta_0\) 和 \(H_1:\theta\in\Theta_0^C\)
- 假设检验：收集样本 \(X=(X_1,...,X_n)\)，制定规则来判断 \(H_0\) 和 \(H_1\) 的真伪。当 \(x\in R\) 时，拒绝 \(H_0\)；否则，接受 \(H_0\).
- 拒绝域：\(R\)
8.2 检验的求法
似然比检验
Def
- 似然比检验 LRT：
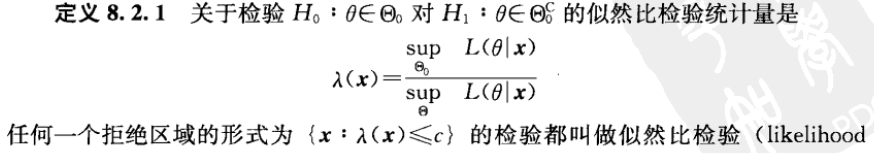
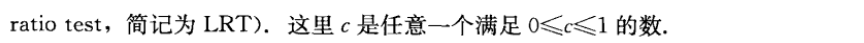
Theorem 8.2.4
Bayes 检验
Def
- Bayes 检验：结合抽样分布 \(f(x|\theta)\) 和先验分布 \(\pi(\theta)\)，我们可以得到后验分布 \(\pi(\theta|x)\)，所有关于 \(\theta\) 的推断都基于后验分布进行。拒绝域 \(R:=\{X\ |\ \mathbb P(\theta\in\Theta_0|X)<\mathbb P(\theta\in\Theta_0^C|X)\}=\{X\ |\ \mathbb P(\theta\in\Theta_0|X)<\frac{1}{2}\}\)
并-交检验和交-并检验
Def
-
并-交检验：
-
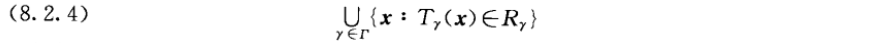
交-并检验：
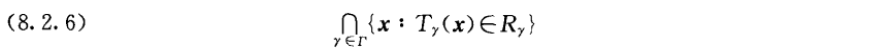
8.3 检验的评价方法
错误概率与功效函数
Def
- 第一类错误：\(H_0\) 成立，但是 \(x\in R\)（拒绝 \(H_0\)）
- 第二类错误：\(H_0^C\) 成立，但是 \(x\in R^C\)（拒绝 \(H_0^C\)）
- 功效函数：\(\beta(\theta)=\mathbb P_\theta(x\in R)\)
- 真实水平/水平：
无偏检验
Def
-
无偏检验：
-
一致最大功效（UMP）检验：
Theorem 8.3.12（Neyman-Pearson 引理）
Ch9 区间估计
Def
- 区间估计：
- 区间可以为闭、开、半开半闭，\(L(x)\) 和 \(U(x)\) 可以取 \(\pm\infty\)
- 覆盖率 CP：\(\mathbb P_\theta(\theta\in[L(X),U(X)])\)
- 陈述是针对 \(X\) 而非 \(\theta\) 的
- 置信系数：\(\inf_\theta \mathbb P_\theta(\theta\in[L(X),U(X)])\)
- 置信区间：区间估计量 + 置信系数
9.2 区间估计量的求法
- 评价标准：限定 \(\inf_\theta \mathbb P_\theta(\theta\in[L(X),U(X)])=1-\alpha,\ \alpha>0\)，使得 \(E(U(X)-L(X))\) 达到最小值。
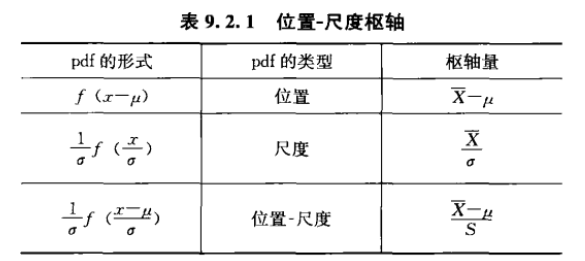
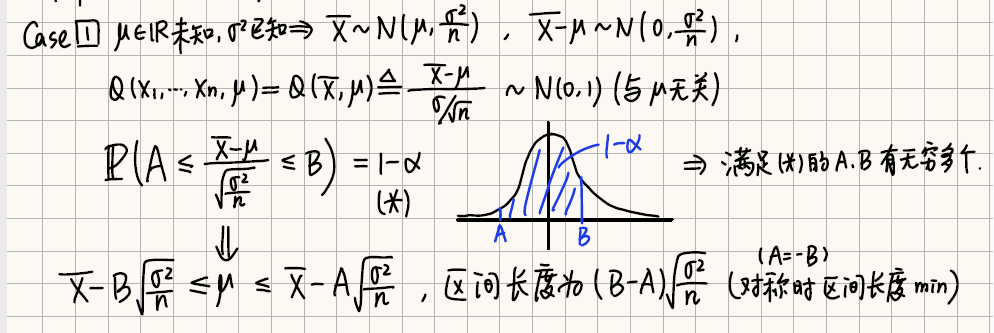
枢轴量法
Def
- 枢轴量：\(Q(X_1,...,X_n,\theta)=Q(T(X),\theta)\) 与 \(X_1,...,X_n,\theta\) 有关，但它的分布与 \(\theta\) 无关，这样的 \(Q\) 被称为枢轴量。
