形式语言与自动机 复习笔记

草，学不完了

预备知识、记号

  • 字母表：形式符号的非空有限集合 \(\Sigma\)。
  • 字符串/串/字：\(\Sigma\) 中字符构成的一个有限序列。空串 \(\varepsilon\)。长度 \(|w|\)。
  • 字符串的运算：
    • 连接 \(xy\)
    • 幂运算 \(\Sigma^n\)（\(\Sigma^0=\{\varepsilon\}\)），*闭包，+闭包
      image
  • 语言：任何集合 \(L\subseteq\Sigma^*\)，空语言 \(\phi\)（区别于“仅含空字的语言” \(\{\varepsilon\}\)）。
  • 语言的运算：
    • 并 \(L\cup M\)
    • 连接 \(L·M\ /\ LM\)
    • 闭包 \(L^*\)

上下文无关文法与上下文无关语言

上下文无关文法的基本概念

  • 四个基本要素：非终结符的集合V；终结符的集合T；产生式的集合P；开始符号S。
  • 形式定义：一个 CFG 是一个四元组 \(G=(V,T,P,S)\)，满足 \(V\cap T=\phi，S\in V\)。
  • 产生式集合的缩写记法：\(A\rightarrow \alpha_1,A\rightarrow \alpha_2,...,A\rightarrow \alpha_n\) 可以简记为 \(A\rightarrow \alpha_1|alpha_2|...|alpha_n\)

归约与推导

  • 归约/递归推理：将产生式右部（body）形式的符号串替换为产生式左部（head）的符号。
  • 推导：将产生式左部的符号替换为产生式右部的符号串。
  • 推导关系 \(\stackrel{\Rightarrow}{G}\)
  • 扩展推导关系到自反传递闭包 \(\stackrel{\stackrel{*}{\Rightarrow}}{G}\)
  • 最左推导，最右推导
  • 句型，左句型，右句型，句子

上下文无关语言

  • 上下文无关文法的语言：设 CFG \(G=(V,T,P,S)\)，定义 G 的语言为 \(L(G)=\{w|w\in T^*\wedge S\stackrel{\stackrel{*}{\Rightarrow}}{G}W\}\)
  • 上下文无关语言

文法与语言的Chomsky分类

  • 0型文法
  • 1型文法
  • 2型文法
  • 3型文法

语法分析树

  • 语法分析树：
    • (1) 每个内部结点由一个非终结符标记。
    • (2) 每个叶结点或由一个非终结符，或由一个终结符，或由 \(\varepsilon\) 来标记。但标记为 \(\varepsilon\) 时，它必是其父结点唯一的孩子。
    • (3) 如果一个内部结点标记为 \(A\)，而其孩子从左至右分别标记为 \(X_1,X_2, …,X_k\)，则 \(A → X_1X_2…X_k\) 是 P 中的一个产生式。注意：只有 \(k=1\) 时上述 \(X_i\) 才有可能为 \(\varepsilon\) ，此时结点 \(A\) 只有唯一的孩子，且 \(A → \varepsilon\) 是 P 中的一个产生式。
  • 语法分析树的果实

归约、推导与分析树之间关系

image

文法和语言中的二义性

  • 二义文法：
    • 定义：CFG \(G = (V, T, P, S )\) 为二义的，如果对某个 \(w\in T^*\)，存在两棵不同的分析树，它们的根结点都为开始符号 S ，果实都为 w 。如果对每一 \(w\in T^*\)，至多存在一棵这样的分析树，则 G 为无二义的。
    • 另一种定义：……，如果存在某个 \(w\in T^*\)，存在两个不同的从开始符号 S 到 w 的最左推导。
  • 语言中的二义性：
    • 固有二义
    • 消除二义性方法：
      • 算符优先级联
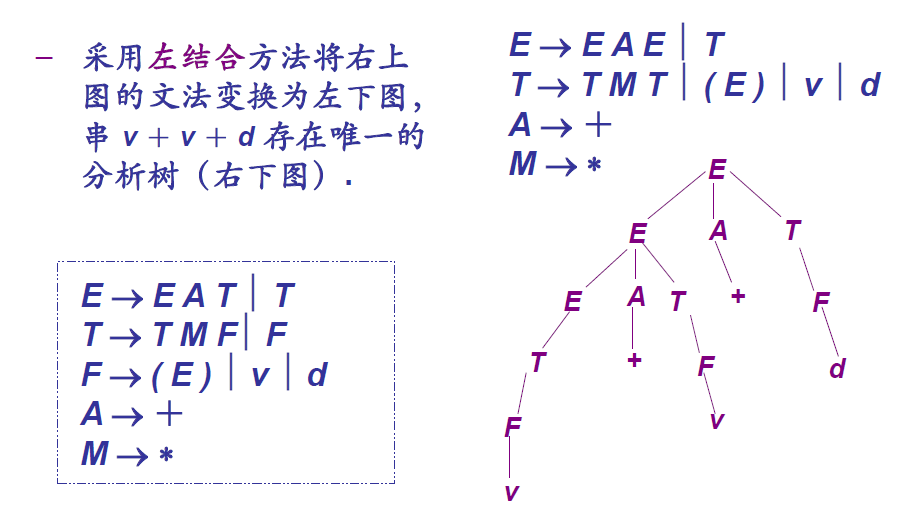
        image
      • 左结合
        image
      • 最近嵌套匹配

正规表达式与正规语言

正规表达式

  • 语法：递归定义
    image
  • 语义
    image
  • 算符优先级：\(*>•>+\)
  • 派生运算符：\(L^+=LL^*=L^*L,L?=\varepsilon+L,L^n,L^0\)

正规语言

  • 定义
    image
    • 利用正规表达式定义：对于字母表 \(\Sigma\) 上的语言 R，若存在 \(\Sigma\) 上的正规表达式 E，满足 \(L(E) = R\)，则 R 是正规语言。

正规表达式的代数定律

  • \(+\) 交换律
  • \(+,•\) 结合律
  • 幺元 \(\varepsilon\)
  • 零元 \(\phi\)
  • \(+,•\) 分配律
  • 等幂律 \(L+L=L\)
  • 代数定律的具体化
    • 具体化：将正规表达式中的每个变量用单个符号替换。
    • 一般化：将具体表达式中的单个符号用变量表示。
    • 结论：正规表达式的一般形式所代表的任何语言与其对应的具体表达式的语言之间可以建立特定的对应关系。

有限状态自动机

确定有限自动机

  • 五要素：有限状态集 \(Q\)，有限输入符号集 \(\Sigma\)，转移函数 \(\delta\)，一个开始状态 \(q_0\)，终态集合 \(F\)
  • 形式定义：DFA 是一个五元组 \(A=(Q,\Sigma,\delta,q_0,F),\delta:Q×\Sigma\rightarrow Q\)
  • 转移图、转移表
  • 扩展转移函数 \(\delta'\)
  • DFA 的语言

非确定有限自动机

  • 形式定义：NFA 是一个五元组 \(A=(Q,\Sigma,\delta,q_0,F),\delta:Q×\Sigma\rightarrow 2^Q\)
  • 扩展转移函数 \(\delta':Q×\Sigma^*\rightarrow 2^Q\)
  • NFA 的语言

DFA 和 NFA 的等价性

  • 定理：L 是某个 DFA 的语言，当且仅当 L 也是某个 NFA 的语言。
    • 从 DFA 构造等价的 NFA
    • 从 NFA 构造等价的 DFA（子集构造法）

应用——文本搜索

带 \(\varepsilon-\)转移的非确定有限自动机

  • 形式定义：\(\varepsilon-\)NFA 是一个五元组 \(A=(Q,\Sigma,\delta,q_0,F),\delta:Q×(\Sigma\cup\{\varepsilon\})\rightarrow 2^Q\)
  • \(\varepsilon-\)闭包 ECLOSE(q)：从 q 经所有的 \(\varepsilon\) 路径可以达到的状态（包括 q 自身）
  • 扩展转移函数 \(\delta':Q×\Sigma^*\rightarrow 2^Q\)
    image
  • ε-NFA的语言
  • ε-NFA 和 DFA 的等价性
    • 从 DFA 构造等价的 ε-NFA
    • 从 ε-NFA 构造等价的 DFA（修改的子集构造法）
      image

（确定）有限自动机的最小化

  • DFA 状态集合上的一个等价关系
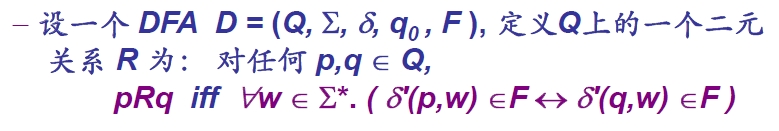
    image

    • 等价，可区别的
    • 几个有用结果：
      image
      image

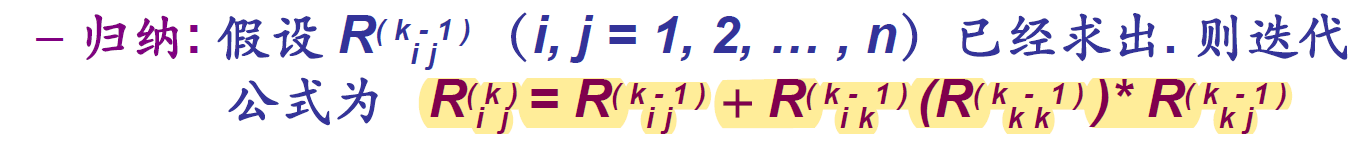
  • 填表法
    image

  • DFA 最小化步骤
    image

  • 最小化的 DFA

有限状态自动机 \(\Leftrightarrow\) 正规表达式

正规表达式 \(\Rightarrow\varepsilon-\)NFA

  • 归纳构造
    • 基础：
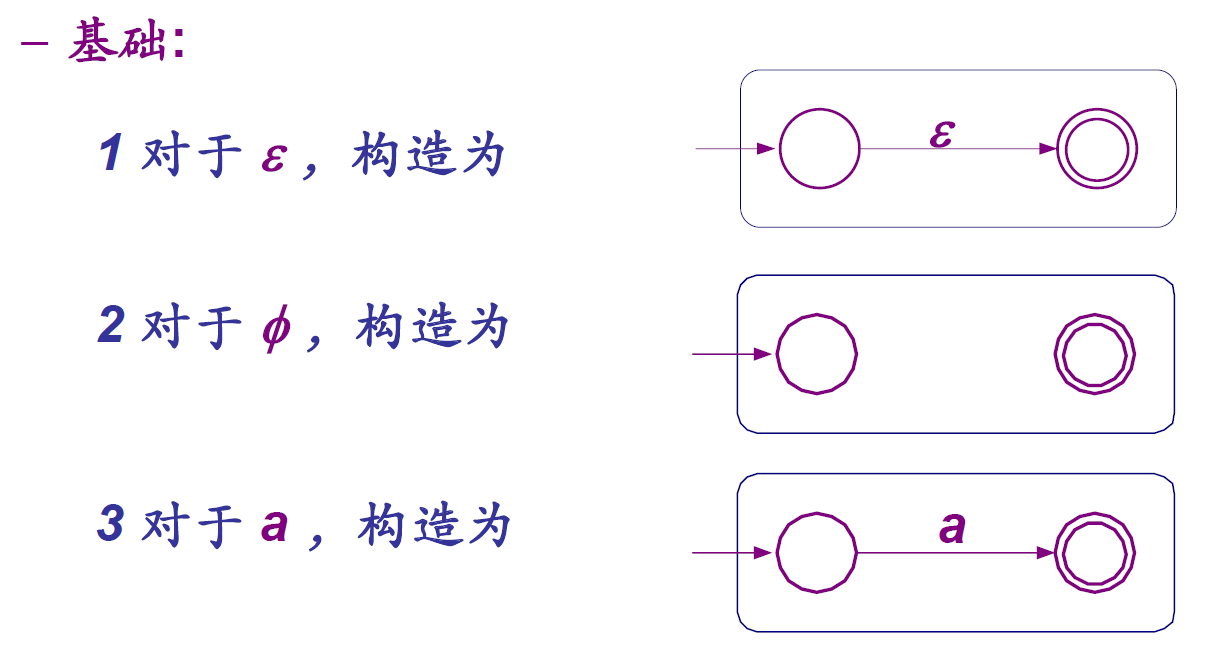
    • 归纳：

DFA \(\Rightarrow\) 正规表达式

  • 路径迭代法


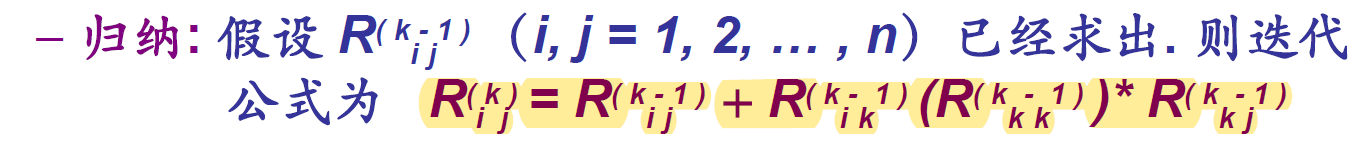
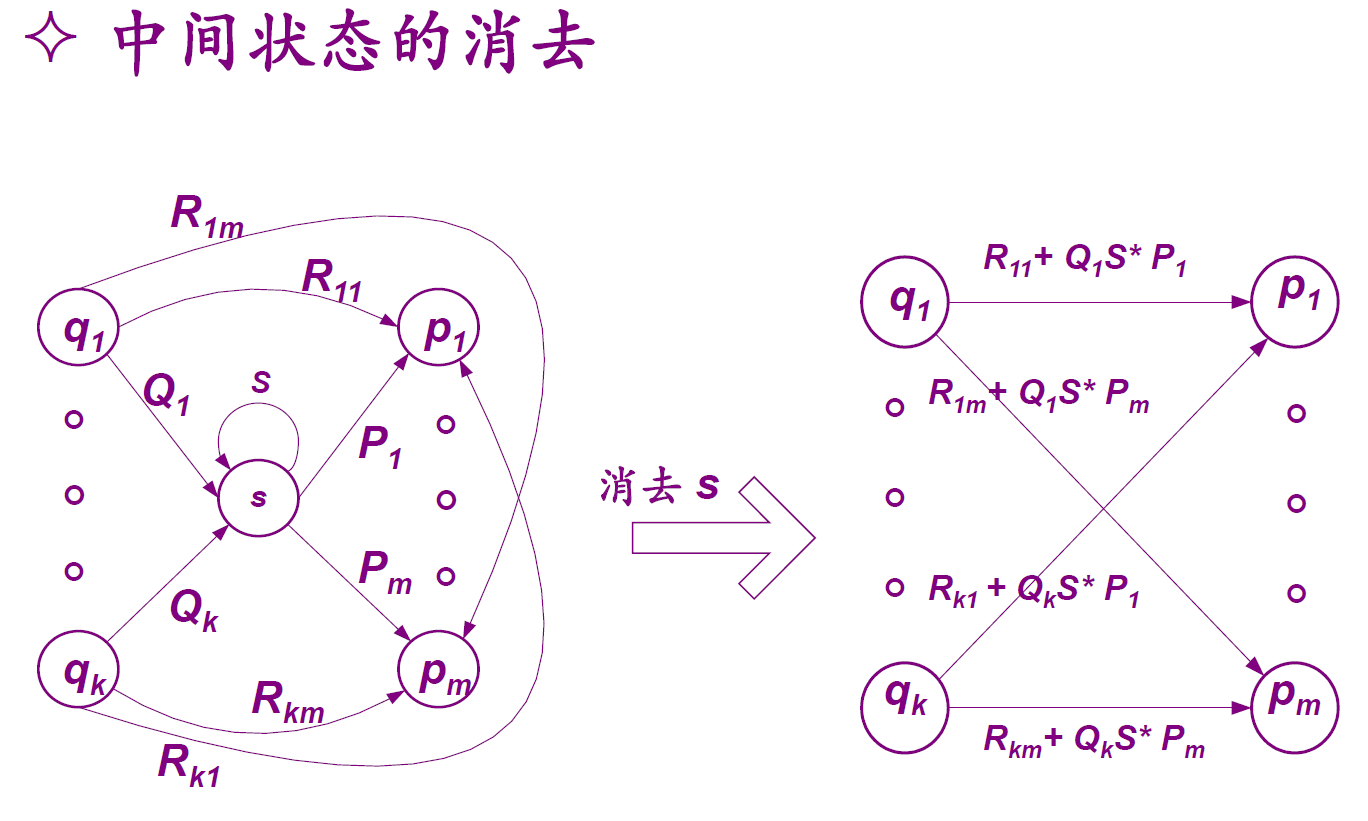
  • 状态消去法

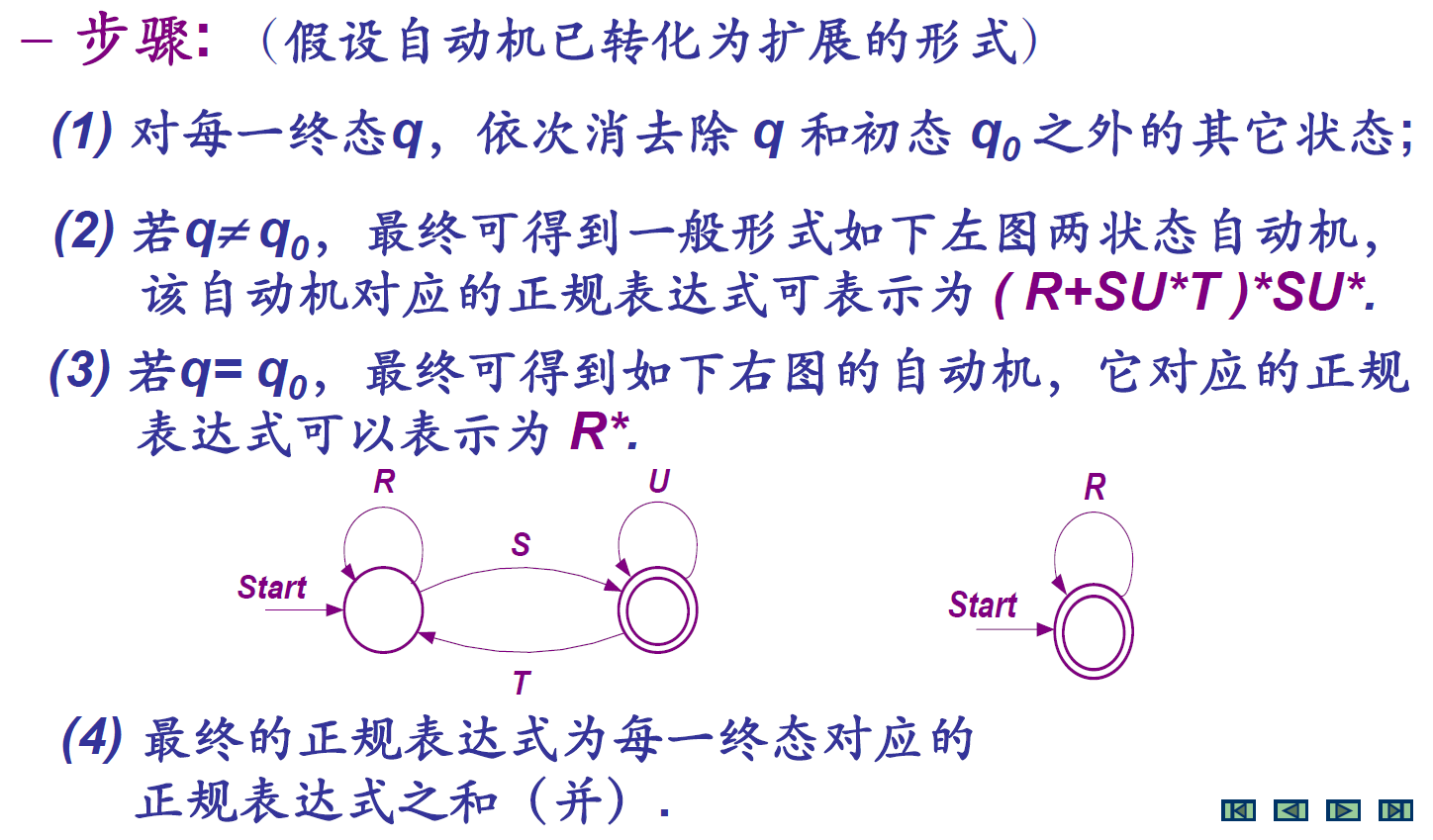
正规语言的性质与运算

Pumping 引理

  • 引理：设 L 是正规语言，则 \(\exist\ const\ n≥1\)，\(s.t.\forall\) 字符串 \(w\in L,\ |w|≥n\)，都可以分成三个部分 \(w=xyz\)，使得
    • \(y\neq\varepsilon\)
    • \(|xy|≤n\)
    • \(\forall k≥0,\ xy^kz\in L\)
  • 应用：用来证明某个语言 L 不是正规语言。步骤：
    • 考虑 \(\forall n≥1\)
    • 找到一个满足下列条件的串 \(w\in L\)（长度至少为 \(n\)）
    • 任选满足 \(w=xyz\wedge y\neq\varepsilon\wedge |xy|≤n\) 的 \(x,\ y,\ z\)
    • 找到一个 \(k≥0\)，使得 \(xy^kz\notin L\)
  • Pumping 引理不是正规语言的充分条件

基本判定性质

  • 判定正规语言是否为空
    • 用有限自动机表示：递归地计算可达状态集合，如果包含终态则非空
    • 用正规表达式
  • 判定正规语言中是否包含特定的字符串
  • 判定两个正规语言是否相等
    • 相并，用填表算法，如果原来的两个 DFA 初态不可区别则相等

关于正规语言的封闭运算

  • 并
  • *闭包
  • 连接
  • 补
  • 交
    • 证明一：de mogan
    • 证明二：构造二元组 DFA
  • 反向
    • 证明一：正规语言
    • 证明二：\(\varepsilon-\)NFA，把所有边反向，初态视为新的终态，新的初态添加 \(\varepsilon\) 转移边指向所有终态
  • 同态，反同态

下推自动机

基本概念

  • 七要素：有限状态集 \(Q\)，有限输入符号集 \(\Sigma\)，有限堆栈符号集 \(\Tau\)，转移函数 \(\delta\)，一个开始状态 \(q_0\)，一个开始堆栈符号 \(Z_0\)，终态集合 \(F\)
  • 形式定义：PDA 是一个七元组 \(P=(Q,\Sigma,\Tau,\delta,q_0,Z_0,F),\delta:Q×(\Sigma\cup\{\varepsilon\})×\Tau\rightarrow 2^{Q×\Tau^*}\)

语言：两种定义

  • 当前格局 \(ID=(q,w,\gamma)=\)（当前状态，剩余的字符串，当前栈中的内容）
  • 终态接受 \(L(P)\)
  • 空栈接受 \(N(P)\)
  • 两种定义的等价性

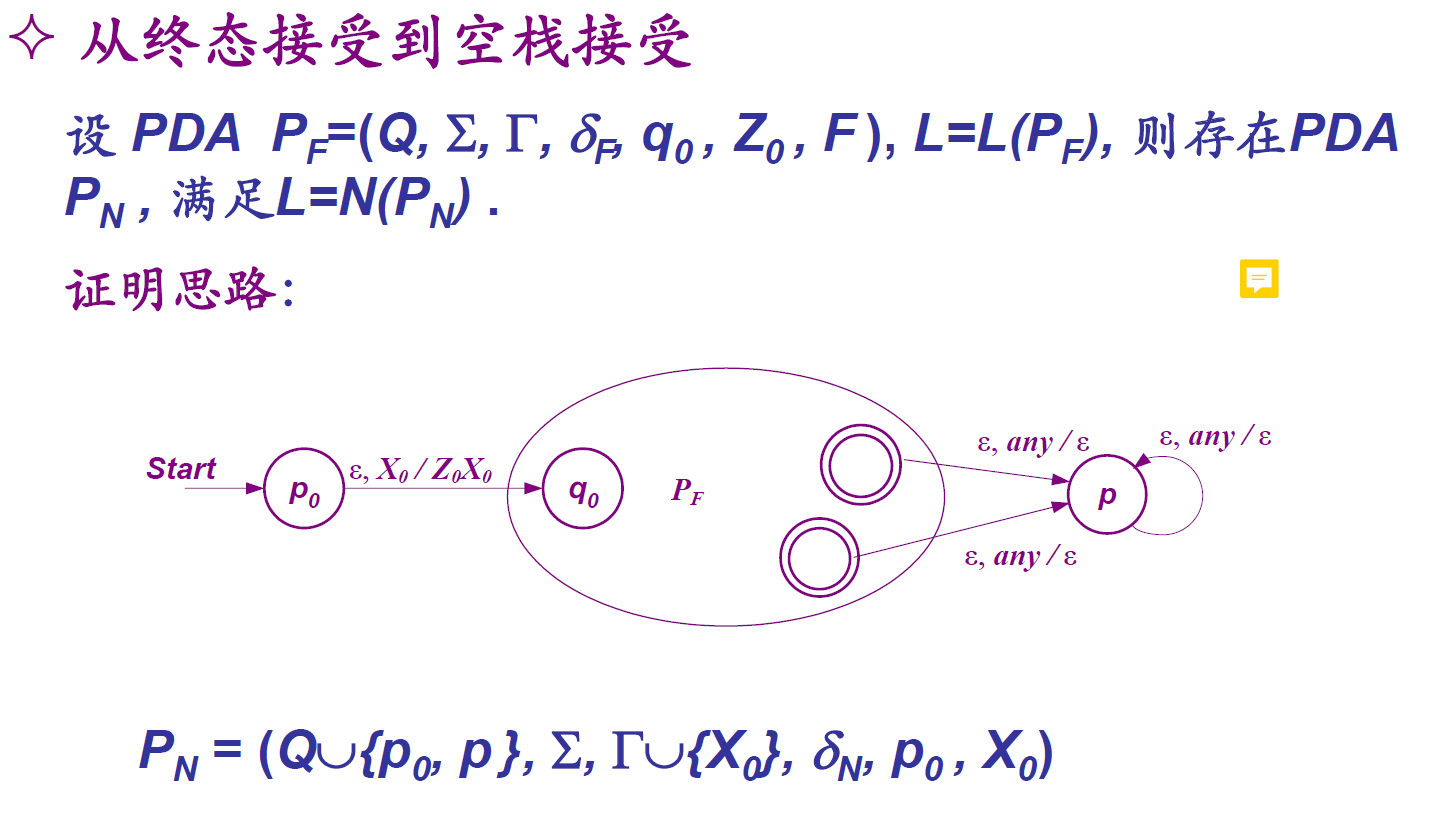
上下文无关文法 \(\Leftrightarrow\) 下推自动机

上下文无关文法 \(\Rightarrow\) 下推自动机

  • CFG \(G=(V,T,P,S)\ \Rightarrow\) 空栈接受 PDA \(E=(\{q\},T,V\cup T,\delta,q,S)\)
    • 转移函数 \(\delta\)
      • 对每一 \(A\in V\)， \(\delta(q,\varepsilon,A)=\{(q,\beta)|“A\rightarrow\beta”\in P\}\)
      • 对每一 \(a\in T\)，\(\delta(q,a,a)=\{(q,\varepsilon)\}\)

下推自动机 \(\Rightarrow\) 上下文无关文法

  • 以空栈方式接受 PDA \(E=(Q,\Sigma,\Tau,\delta,q_0,Z_0)\Rightarrow\) CFG \(G=(V,\Sigma,P,S)\)
    • \(V=\{S\}\cup\{[pXq]|p,q\in Q\wedge X\in\Tau\}\)
    • 产生式集合 \(P\)
      • 对每一 \(p\in Q\)，G 包含产生式 \(S\rightarrow[q_0Z_0p]\)
      • 若 \((q,X_1X_2…X_k)\in\delta(p,a,X)\)，则 G 包含产生式 \([pXp_k]→a[qX_1p_1][p_1X_2p_2]…[p_{k-1}X_kp_k]\)，其中 \(a\in\Sigma\) 或 \(a=\varepsilon\)

确定下推自动机

概念

  • 形式定义：DPDA 是一个七元组 \(P=(Q,\Sigma,\Tau,\delta,q_0,Z_0,F)\)，其中
    • 对于 \(a\in\Sigma\) 或 \(a=\varepsilon\)，\(X\in\Tau\)，\(\delta(q,a,X)\) 中最多包含一个元素
    • 对于 \(a\in\Sigma\)，若 \(\delta(q,a,X)\neq\phi\)，则 \(\delta(q,\varepsilon,X)=\phi\)

确定下推自动机和正规语言

  • DPDA 的计算能力强于有限自动机
    • 若 L 为正规语言，则存在 DPDA P，L(P) = L
    • 语言 \(\{L_{wcwr} = wcw^R | w 为 0,1 字符串 \}\) 不是正规语言（可由 Pumping 引理证明），但它是某一 DPDA 的语言。

前缀性质及空栈接受的 DPDA

  • 前缀性质：一个语言 L 具有前缀性质（prefix property）当且仅当不存在 \(x,y\in L,x\neq y\), 且 \(x\) 为 \(y\) 的前缀 (prefix)
  • 结论：一个语言 L 是某个空栈接受的 DPDA P 的语言，即 L = N(P)，当且仅当 L 具有前缀性质，并且 L 是某个 DPDA P' 的语言，即 L = L(P')

DPDA 和上下文无关语言

  • 结论：某些上下文无关语言，不是任何 DPDA 的语言
  • 定义：若上下文无关语言 L 是某个 DPDA 的语言，则称 L 为一个确定的上下文无关语言（deterministic context free language）

DPDA 和无二义文法

  • 结论：一个语言 L 是某个空栈接受的 DPDA P 的语言，即 L = N(P)，则 L 存在一个无二义文法
  • 结论：一个语言 L 是某个 DPDA P 的语言，即 L = L(P)，则 L 存在一个无二义文法
  • 结论：固有二义的语言不是任何 DPDA 的语言

几类语言模型的计算能力对比

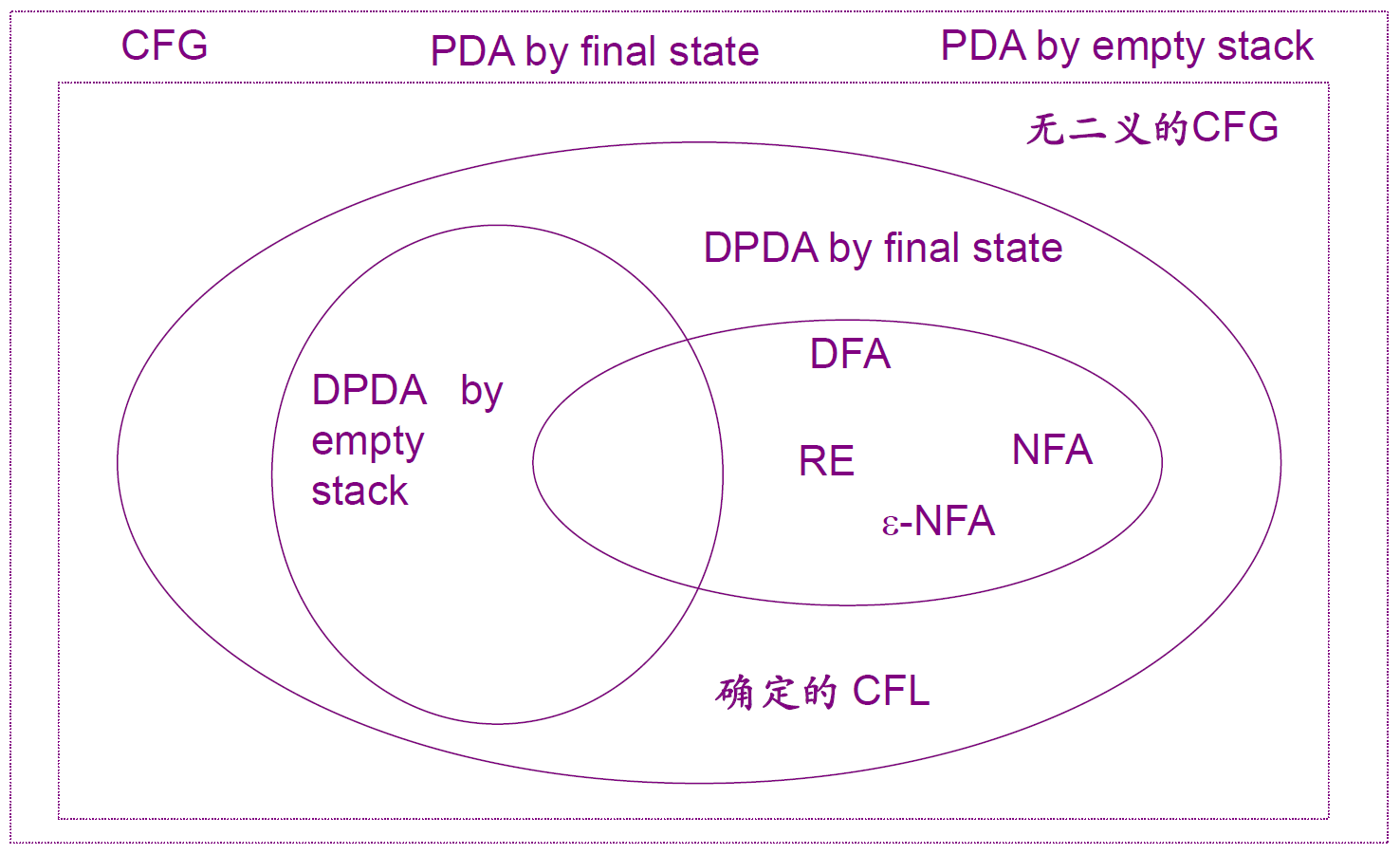
CFG 的简化及 Chomsky 范式

消去无用符号

  • 有用符号：
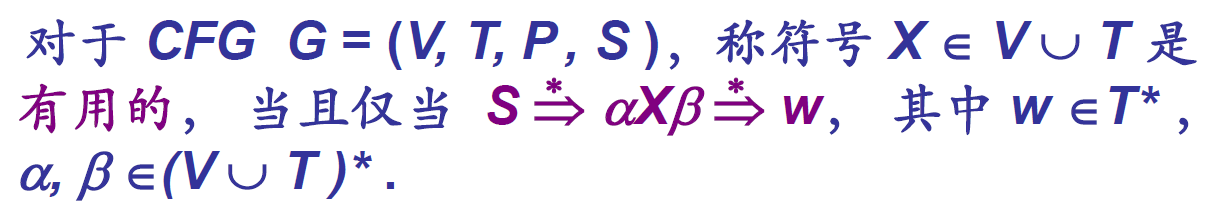
  • 无用符号
  • 生成符号，可达符号
    • 有用符号一定是生成符号和可达符号
  • 消去非生成符号及不可达符号步骤
    • 计算生成符号集合（终结符都是生成符号；往前推导）
    • 计算可达符号集合（开始符号是可达符号；往后推导）
    • 消去非生成符号
    • 消去不可达符号

消去 \(\varepsilon\) 产生式

  • 可致空符号
  • 消去 \(\varepsilon\) 产生式及所有可致空符号的影响步骤
    • 计算可致空符号集合（直接推出空为可致空符号；往前推导）
    • 对每一产生式 \(A\rightarrow A_1A_2...A_k\) 在 \(G_1\) 中对应有一组产生式，每一个可致空符号都可能出现或不出现；若包含 \(m < k\) 个可致空符号，则该产生式能够对应 \(G_1\) 中的 \(2^m\) 个产生式；若包含 \(k\) 个可致空符号，则该产生式能够对应 \(G_1\) 中的 \(2^{k-1}\) 个产生式
    • \(G_1\) 中不包含 \(G\) 的所有 \(\varepsilon\) 产生式

消去 Unit 产生式

  • Unit 产生式，Unit 偶对
  • 消去 Unit 产生式步骤
    • 计算 Unit 偶对的集合（非终结符 \(A\rightarrow A\) 是 Unit 偶对；往双方推）
    • 对每个 Unit 偶对 \((A,B)\)，在 \(G_1\) 中加入产生式 \(A\rightarrow \alpha\)，其中 \(B\rightarrow \alpha\) 为一个非 Unit 产生式
    • \(G_1\) 中包含 \(G\) 的所有非 Unit 产生式

CFG 的简化

  • 步骤
    • 先消除 \(\varepsilon\) 产生式
    • 再消除 Unit 产生式
    • 最后消除无用符号
  • 结论：设 CFG G 的语言至少包含一个非 \(\varepsilon\) 的字符串，通过上述步骤从 \(G\) 构造 \(G_1\)，则有 \(L(G_1) = L(G)\)

Chomsky 范式

  • Chomsky 范式 CNF
  • 得到范式步骤
    • 得到不含 \(\varepsilon\) 产生式、不含 Unit 产生式以及不含无用符号的文法 \(G_2\)
    • 如果某一终结符 a 出现于某些右部长度大于 1 的 产生式中，则引入一个新的非终结符，如 A，将这些产生式中的 a 替换为 A，并增加新的产生式 \(A\rightarrow a\)。至此，右部长度大于 1 的产生式中只包含有非终结符
    • 将右部长度大于 2 的产生式采用级连的方法转变为只包含两个非终结符

上下文无关语言的性质与运算

Pumping 引理

  • 引理：
  • 应用：
  • Pumping 引理不是上下文无关语言的充分条件

有关上下文无关语言的判定性质

  • 判定上下文无关语言是否为空
    • 计算所有生成符号的集合
    • 判定文法的开始符号是否生成符号；若是，则该文法表示的上下文无关语言非空；否则，该语言为空
  • 判定上下文无关语言中是否包含特定的字符串
    • 将该文法变换为符合 Chomsky 范式
    • 采用 CYK 算法判定该文法所产生的语言是否包含字符串 w

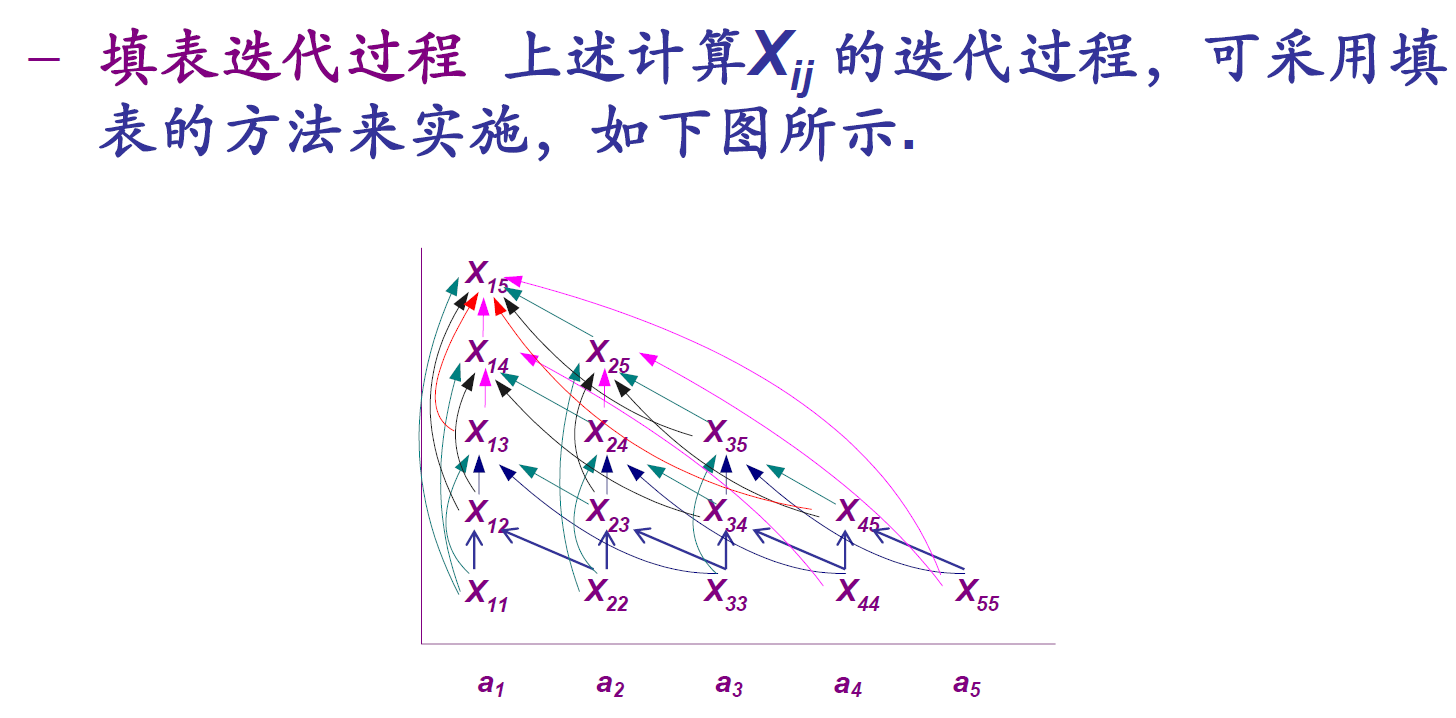
关于上下文无关语言的封闭运算

  • 替换
  • 并
  • 反向
  • 闭包（星闭包和正闭包）
  • 连接
  • 同态
  • 反同态
  • 与正规语言的交
    • 两个上下文无关语言的交不一定是CFL！

图灵机与递归可枚举语言

图灵机的概念与定义

递归可枚举语言

posted @ 2022-11-13 08:51  SELFLOVER  阅读(579)  评论(0)  编辑  收藏  举报