离散数学(2) 复习笔记
Ch1 基本概念
1.1 图的概念
图:二元组 (V(G), E(G)) ,节点集,边集。 G = (V, E)。有限图,无限图。
有向边 | 弧,无向边。相邻结点,相关联。始点,终点,直接前驱,直接后继。端点。有向图,无向图,混合图。自环,重边。多重图。
度 d(v),正度 d^+(v) (发出的边),负度 d^-(v) (接收的边)。
简单图,空图 N_n,完全图 K_n。

权,赋权图,正权图。
子图,支撑子图(V' = V),导出子图。平凡子图。
图的并、交、对称差。G - H,补图G(上划线),G - v,G - e。
邻点集,直接后继集 | 外邻集 ![]() ,直接前驱集 | 内邻集
,直接前驱集 | 内邻集 ![]() 。
。
同构。


1.2 图的代数表示
邻接矩阵(可以表示自环,无法表示重边)
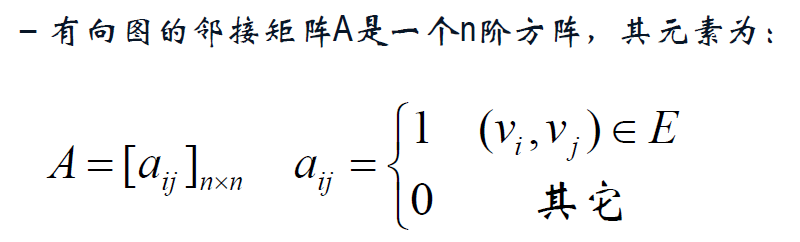
权矩阵(可以表示自环,无法表示重边)
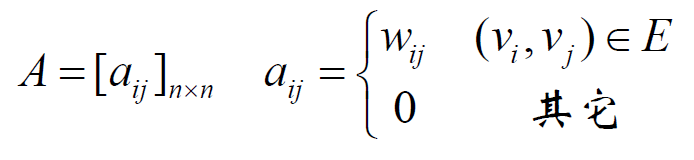
关联矩阵(可以表示重边,无法表示自环)
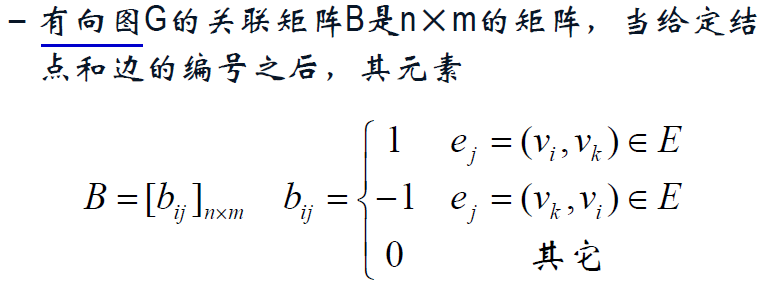
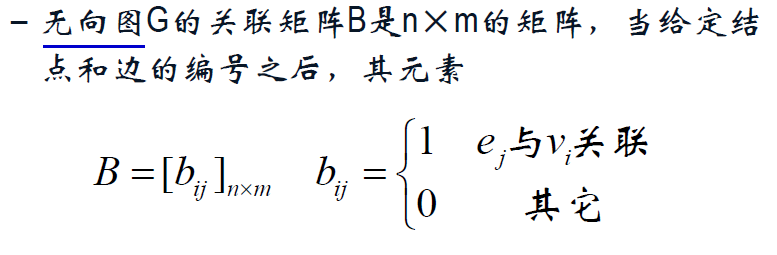
边列表

正向表



逆向表

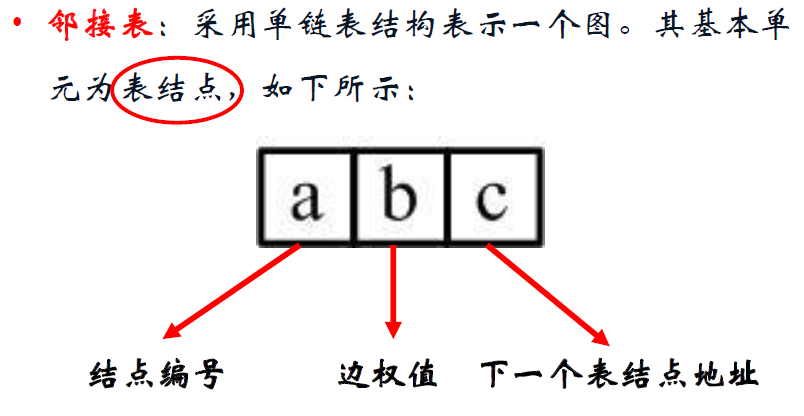
邻接表

Ch2 道路与回路
2.1 道路与回路
有向道路,有向回路,简单有向道路(回路),初级有向道路(回路) | 路(回路)。
链 | 道路,圈 | 回路,简单道路(回路),初级道路(回路)。
连通图,非连通图,连通支。

2.2 道路与回路的判定
邻接矩阵法

Warshall算法
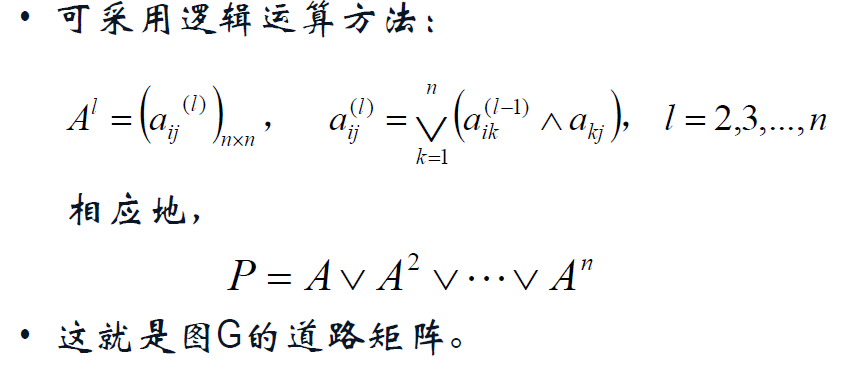

搜索法(BFS / DFS)
2.3 欧拉道路与回路
欧拉回路(道路)
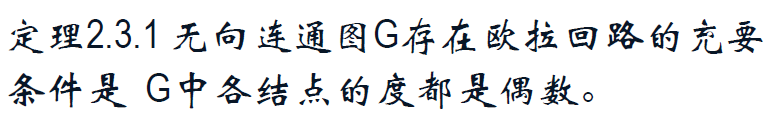

2.4 哈密顿道路与回路
哈密顿回路(道路) | H回路(道路)
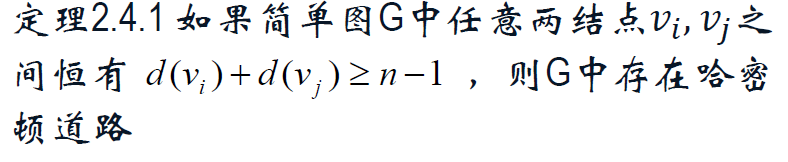
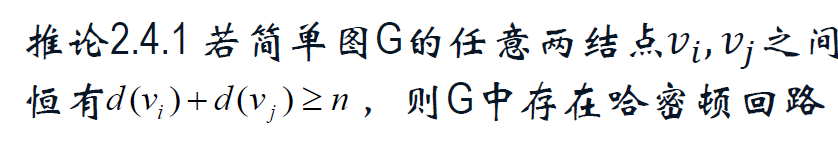

G的闭合图 C(G)
![]()

2.5 旅行商问题
旅行商问题 | TSP | TS:给定一个正权完全图,求其总长最短的哈密顿回路,就是TSP问题。
分枝与界法。

2.6 最短路径
① 权值均大于0:正权图 —— Dijkstra算法
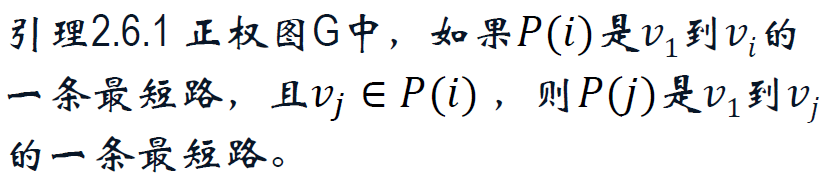



② 权值均等于1 —— 广探法
③ 权值为任意实数 —— Ford算法

2.7 关键路径
PT图:用结点表示工序,如果工序 i 完成之后工序 j 才能启动,则图中有一条有向边 (i, j),其长度 w_i 表示工序 i 所需的时间。



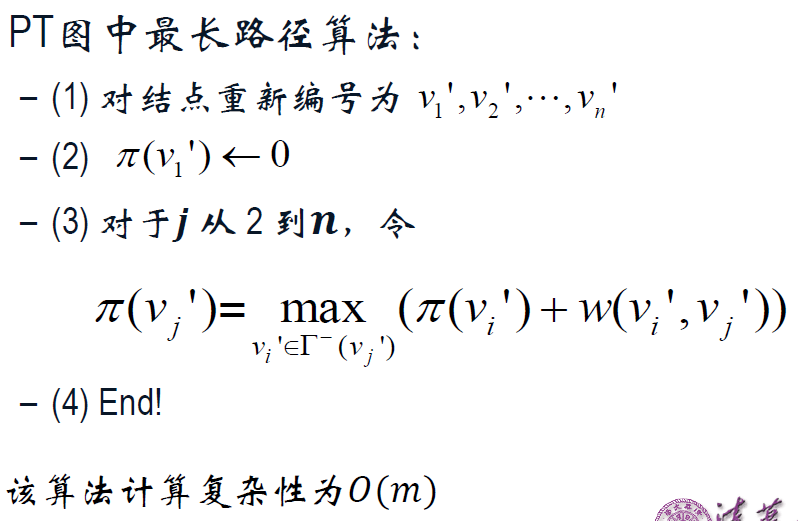

![]()
a. τ(v_n') = π(v_n')
b. 对 j 从 (n-1) 到 1,令 τ(v_j') = min ( τ (v_i') - w(v_j', v_i') ),其中 v_i' 是 v_j' 的直接后继。
PERT图:采用有向边表示工序,其权值表示该工序所需时间,如果工序 e_i 完成后 e_j 才能开始,则令 v_k 是 e_i 的终点,e_j 的始点。
最早完工时间是 v_1 到 v_n 的最长路径长度,这条路径就是关键路径。工序 e_k = (v_i, v_j) 的最晚启动时间是 τ(v_i, v_j) = π(v_n) - π(v_j, v_n) - w(v_i, v_j)。
Ch3 树
3.1 树的有关定义
树,树枝,树叶。割边。


支撑树 | 生成树,余树。
3.2 基本关联矩阵及其性质
基本关联矩阵 B_k。
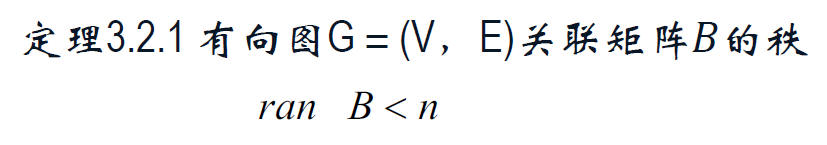

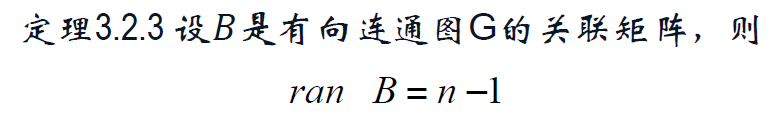
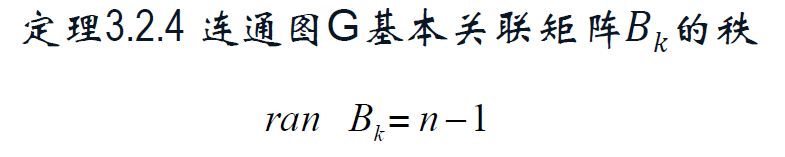



3.3 支撑树的计数

① 有向连通图的树计数

G 中不含某特定边 e 的树的数目:作 G - e。
G 中必含某特定边 e 的树的数目:收缩结点。
② 无向连通图的计数
对无向连通图G的每边任给一方向,便得到相应的有向连通图G',计算G'的树即可。
③ 有向连通图G根树的计数
根树:任何以 v_0 为根的根树的基本关联矩阵 B_0 中一定是每行每列都只有一个 -1 元素。
重新编号后,可以让基本关联矩阵变成一个上三角矩阵,-1 元全是对角元,因此把1改为0之后行列式不变。这正是根树的特征。
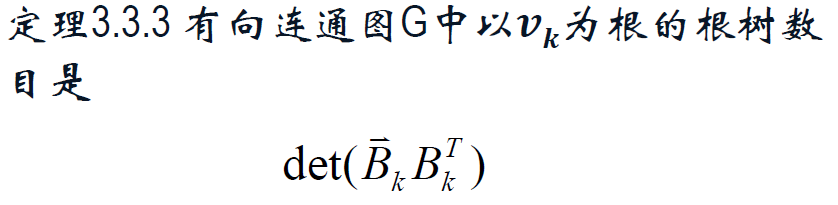

3.4 回路矩阵与割集矩阵
① 回路矩阵
正向边,反向边。
完全回路矩阵 C_e。

基本回路,基本回路矩阵 C_f。
基本回路矩阵的秩是 m - n + 1。
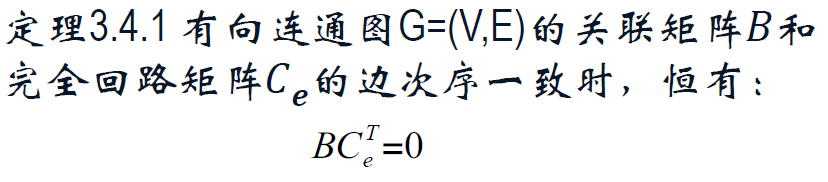
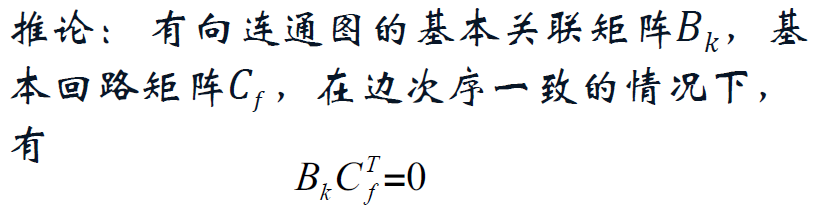
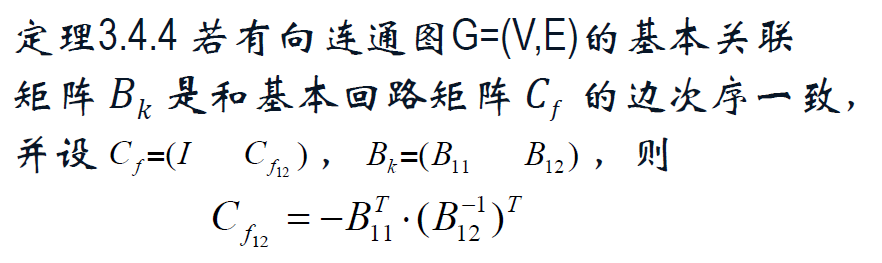
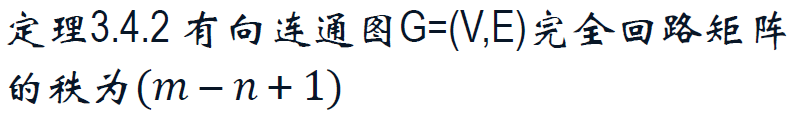
回路矩阵。


② 割集矩阵
割集,有向割集。
完全割集矩阵 S_e。

基本割集,基本割集矩阵 S_f。
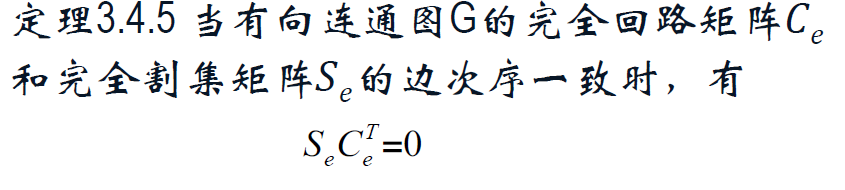
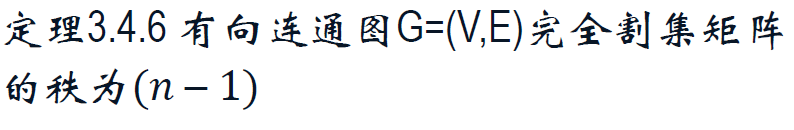
割集矩阵




3.5 支撑树的生成
树的距离,基本树变换。

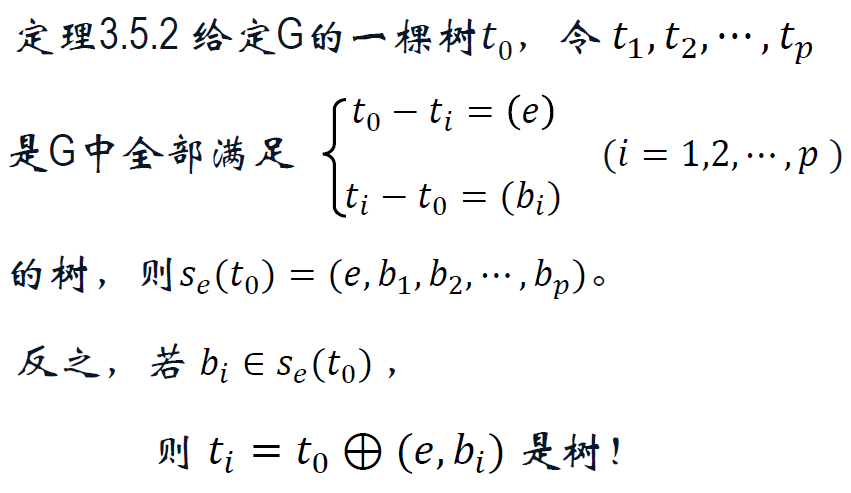
T^e


T^(e_i)(e_j) = { t ⊕ (e_j, b) | b 属于 e_i 生成的割集与 e_j 生成的割集的并,t 属于 T^(e_i),b ≠ e_j }
3.6 Huffman树
二叉树,完全二叉树,赋权二叉树,最优二叉树。

3.7 最短树
① Kruskal (克鲁斯卡尔)算法



② Prim (普林)算法
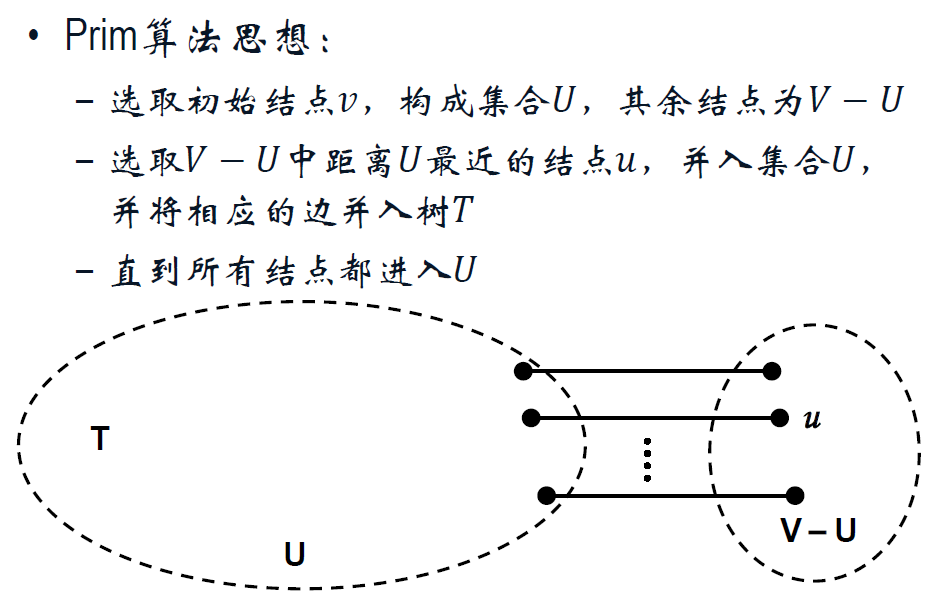



③ 破圈法
一直找回路,去掉最长边。
Ch4 平面图与图的着色
4.1 平面图
可嵌入平面 | 可平面图,平面图。
面 | 域,边界。无限域,内部域。相邻。
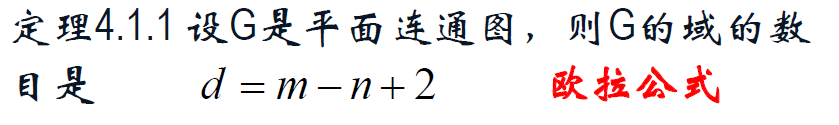


4.2 极大平面图
极大平面图。



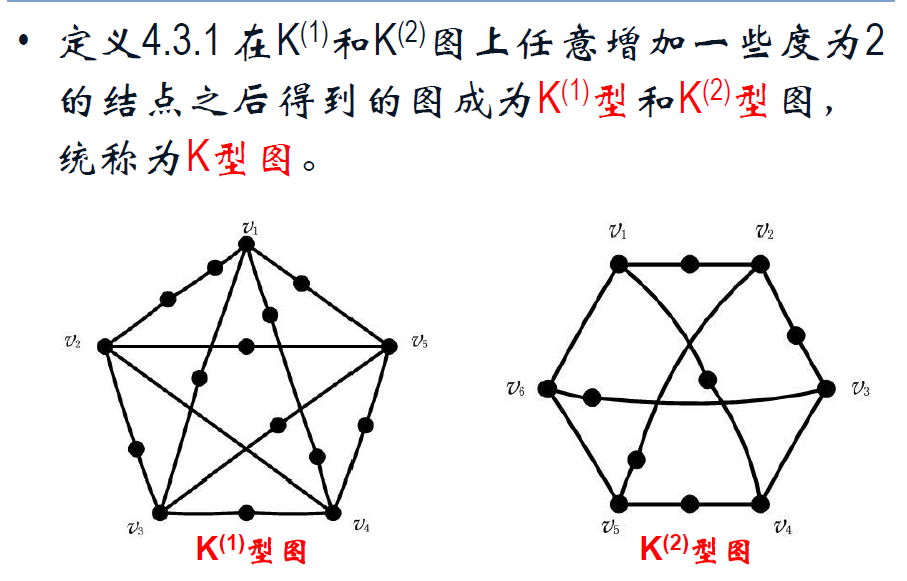
4.3 非平面图
二分图 | 二部图。非平面图。
![]()
![]()
K型图
![]()
库拉图斯基(Kuratowski)定理

4.4 图的平面性检测

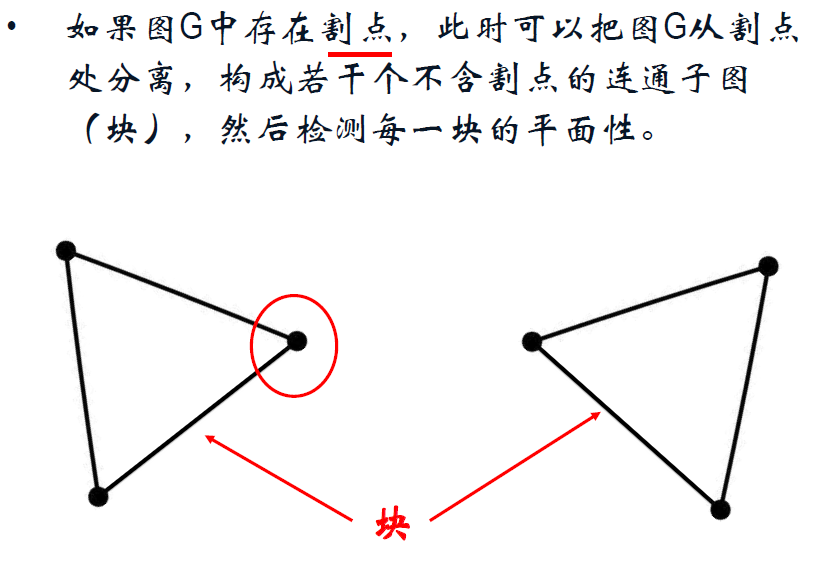

DMP 算法。
4.5 对偶图
对偶图。




![]()
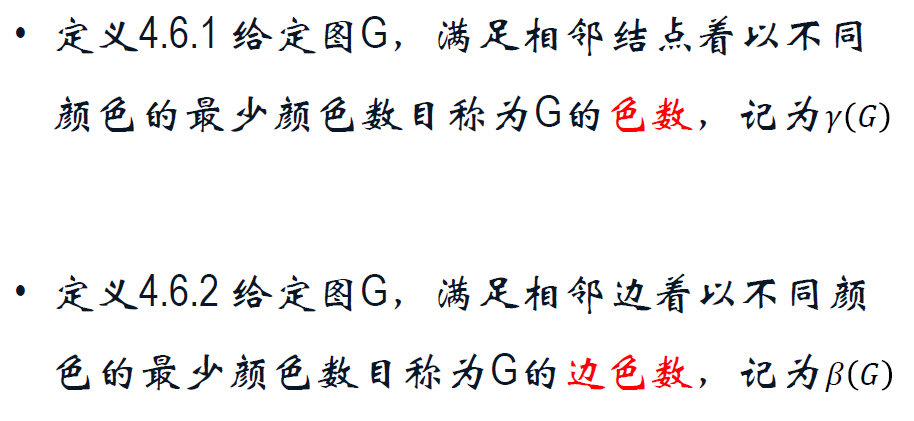
4.6 色数与色数多项式
色数,边色数。
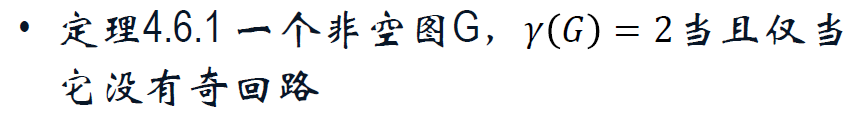
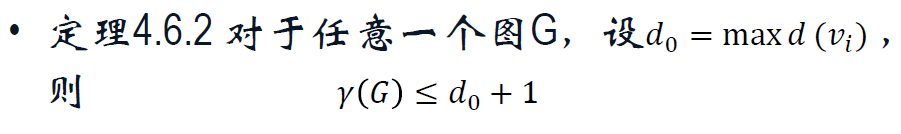
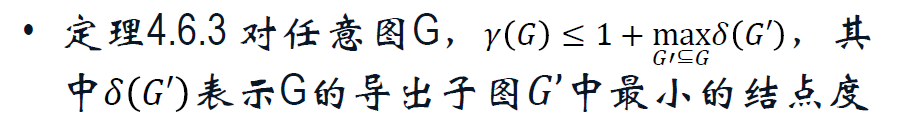
G_ij(上划线,上加点)


色数多项式


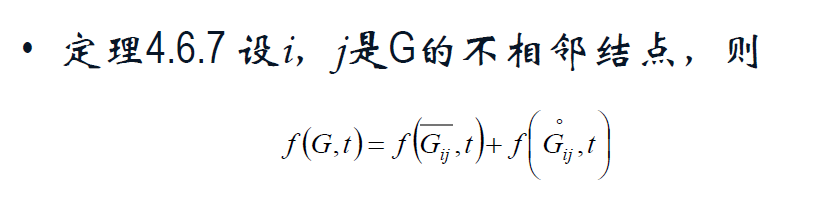
Ch5 匹配与网络流
5.1 二分图的最大匹配
匹配,饱和点,不饱和点。
最大匹配。交互道路,可增广道路。

匈牙利算法


5.2 完全匹配
完全匹配,完美匹配。

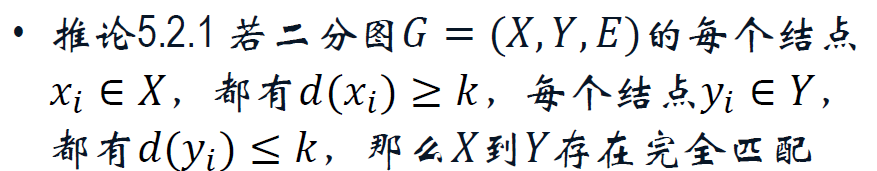

最小覆盖数。

5.3 最佳匹配及其算法
最佳匹配。
最大权匹配算法

最小权匹配 | 最小成本。
5.5 网络流图
运输网络 | 网络流图,源 s,汇 t,容量 c_ij 。允许流,边流量 f_ij,流量w。

饱和边,非饱和边。最大流。
割切 (S, S上划线),割切的容量 C(S, S上划线)。

增流路径:① 如果从 s 出发,沿途的向前边都不饱和,直到 t 都是如此,那么该路径一定可增流;② 如果从 s 出发,沿途向前边不饱和,向后边流量大于零,直到 t 都是如此,那么该路径一定可以增流。
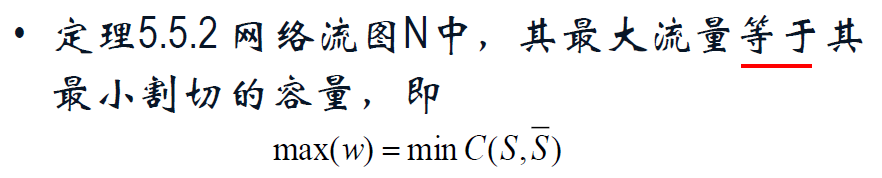
5.6 Ford-Fulkerson最大流标号算法




5.7 最大流的Edmonds-Karp算法

Ch7 代数结构预备知识
7.1 集合与映射
基数,幂集。分配律。
映射,定义域,值域,象,原象,f 的象。
映射相等(值域、定义域、对应方式相等)。
单射,满射,双射。
映射的合成(一般不满足交换律,但是满足结合律)。
恒等映射。
左可逆映射,右可逆映射,左逆映射,右逆映射,可逆映射。


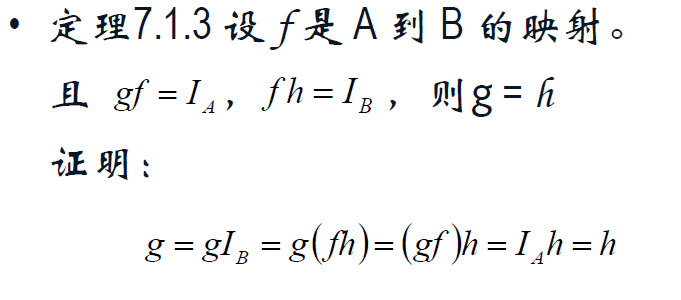
7.2 等价关系
笛卡尔积。二元关系。等价关系 ~ ,等价类 a上划线,代表元,等价类族 A上划线,商集 A/~,自然映射。
7.3 代数系统的概念
二元运算,n元运算。代数系统 | 代数结构 | 代数 (A, f_1, f_2, ..., f_s),有限代数系统。
* 判定一个给定的系统是代数系统:① 定义的运算应该满足映射成立条件;② 所有运算的封闭性。 *
交换律,结合律 -> 指数律。
左单位元,右单位元。

左可逆,右可逆,左逆元,右逆元,可逆元。

每个元都有逆元 -> 消去律。
7.4 同构与同态
同类型,同构![]() ,同态。
,同态。
子代数系统 | 子代数,同态象。
单一同态,满同态 X~Y

自同态,自同构。
Ch8 群
8.1 半群
半群,含幺半群 | 幺群,交换幺群,循环幺群,生成元。
![]()
子半群,子幺群。同态,单同态,满同态,同构。

8.2 群、群的基本性质
群,交换群 | 阿贝尔(Abel)群。



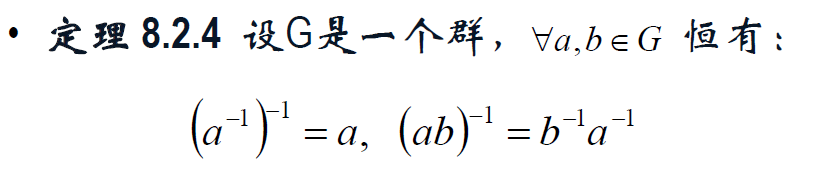
阶 | 周期 O<a>,有限阶元素。

子群,平凡子群,真子群 H<G。

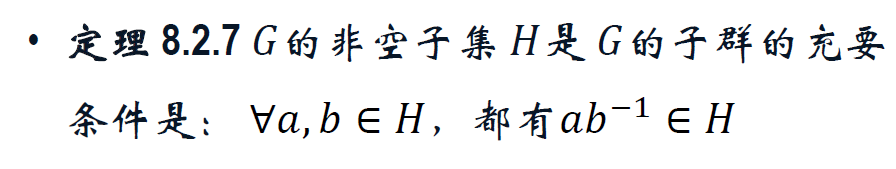
8.3 循环群 群的同构
循环群 <a>,生成元。
n 阶循环群,无限阶循环群。




![]()

8.4 交换群和置换群 Cayley定理
变换,全部变换的集合 M(A),一一变换。
变换的乘积 | 乘法运算(符合结合律)。一一变换群 E(A),变换群。
n 元置换(有限集合中的一一变换),置换群。
n 次对称群 S_n,n 元置换群。
轮换,恒等置换,对换。
不相交的轮换。


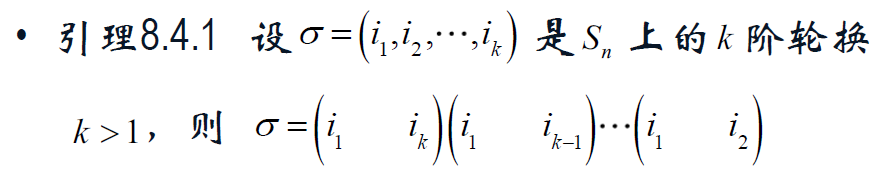
逆序,逆序数。

奇置换,偶置换。交错群。

8.5 陪集和群的陪集分解 Lagrange定理
(子群 H 在 G 中的一个)左陪集,右陪集。


H 在 G 中的指数 [G:H]


![]()

8.6 正规子群与商群
正规子群 | 不变子群 H⊴G,陪集。



8.7 群的同态、同态基本定理
同态映射 | 同态,单一同态,满同态 G_1 ~ G_2,同构,同态象。
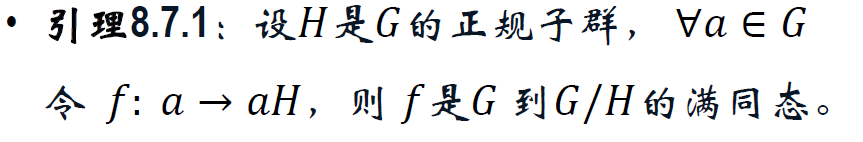


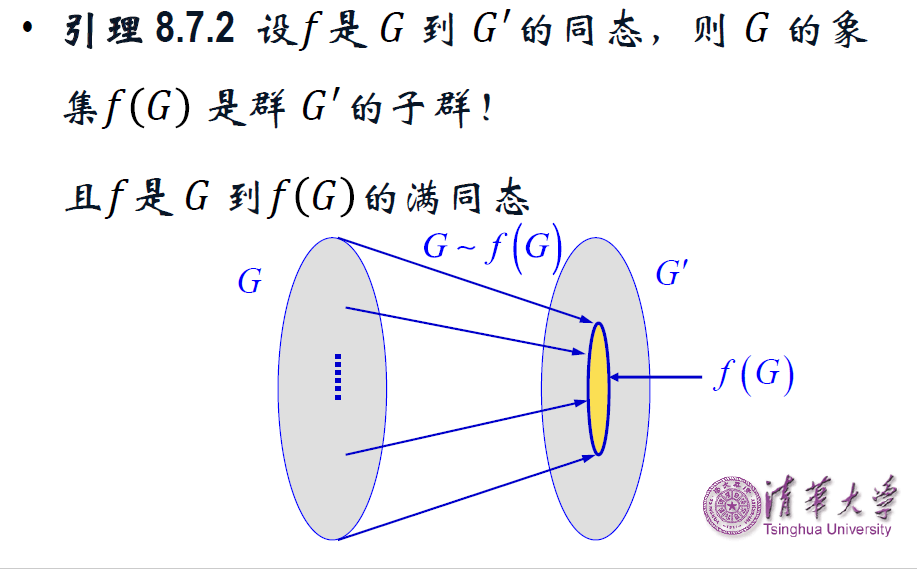
(群的同态象仍然是群)



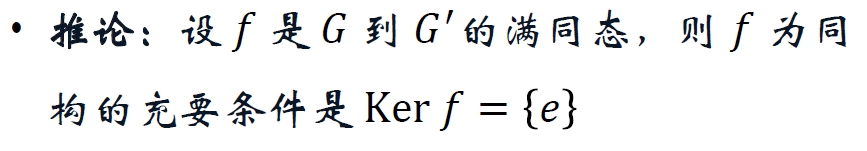



 浙公网安备 33010602011771号
浙公网安备 33010602011771号