高等线性代数(2) 复习笔记(已中道崩殂)
第六章 特征值
6.0 线性变换与矩阵
线性变换的相关概念
线性变换的矩阵表示:(σ(α_1),σ(α_2),...,σ(α_n))=(α_1,α_2,...,α_n)*A;(α_1,...,α_n)到(β_1,...,β_n)的过渡矩阵为P(即(β_1,...,β_n)=(α_1,...,α_n)*P),σ在α下的表示矩阵为A,在β下的表示矩阵为P,则B=P^(-1)AP
6.1 特征值和特征向量
定义6.1.1 (线性变换的)特征值,特征向量
定义6.1.2 (矩阵的)特征值,特征向量,特征子空间
定义6.1.3 (矩阵的)特征多项式
定理6.1.1 若A和B相似,则A与B具有相同的特征多项式,从而具有相同的特征值(计重数)。
定义6.1.4 (线性变换的)特征多项式
* Vieta定理 -> λ_1+λ_2+...+λ_n = trA,λ_1*λ_2*...*λ_n = |A| *
* 求矩阵特征值和特征向量的方法:作矩阵λI-A并求出特征多项式|λI-A|的根(A的特征值),将每个特征值代入线性方程组(λI-A)x=0求出非零解,就是关于特征值λ的特征向量。 *
* 对数域K上的矩阵(或相应的线性变换),有可能在K中不存在特征值。 *
定理6.1.2 任一复方阵必(复)相似于一上三角阵。
证明:对矩阵阶数归纳。
命题6.1.1

命题6.1.2
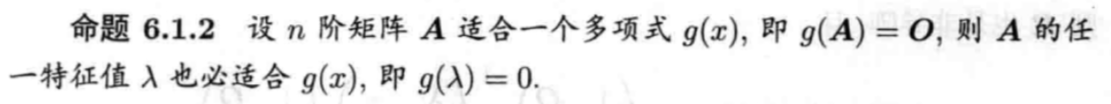
命题6.1.3

6.2 对角化
定理6.2.1 n阶方阵A相似于对角阵的充分必要条件是A有n个线性无关的特征向量(这样的矩阵称为可对角化矩阵)。
定理6.2.2 n维线性空间V上的线性变换φ存在一组基使得它在这组基下的表示矩阵为对角阵 等价于 φ有n个线性无关的特征向量(这样的线性变换称为可对角化线性变换)。
定理6.2.3
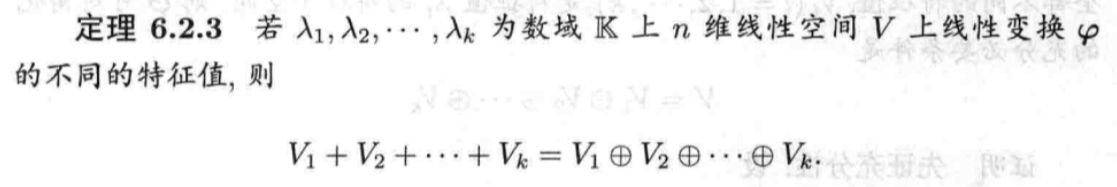
推论6.2.1 线性变换φ属于不同特征值的特征向量必线性无关。
推论6.2.2 若n维线性空间V上的线性变换φ有n个不同的特征值,则φ必可对角化。 | 若线性变换φ的特征多项式没有重根,则φ可对角化。
* 推论6.2.2是充分不必要条件。 *
推论6.2.3

定义6.2.1 度数 | 几何重数,重数 | 代数重数
引理6.2.1 线性变换φ的特征值λ度数总是小于其重数。
证明:使用基扩张定理以及矩阵分块。
定义6.2.2 完全的特征向量系
定理6.2.4 φ可对角化 等价于 φ有完全的特征向量系。
* 求P使得P^(-1)AP为对角阵:只要求出A的n个线性无关的特征向量,把它们放在一起组成一个矩阵就是要求的P。*
6.3 极小多项式与Cayley-Hamilton定理
定义6.3.1 (矩阵或线性变换的)极小多项式
引理6.3.1 m(x) | f(x)
命题6.3.1 任一n阶矩阵的极小多项式唯一。
命题6.3.2 相似的矩阵具有相同的极小多项式。
证明:只要证明两个极小多项式互相整除即可。
命题6.3.3

证明:只要证明两个式子互相整除即可。
例6.3.2 设n阶方阵A可对角化,λ_1,λ_2,...,λ_k是A的全部不同特征值,则A的极小多项式为(λ-λ_1)(λ-λ_2)...(λ-λ_k)。
引理6.3.2 (x-λ_0) | m(x)
定理6.3.1

证明:利用引理:对n阶上三角阵A,f(A)=O。
推论6.3.1

推论6.3.2

推论6.3.3
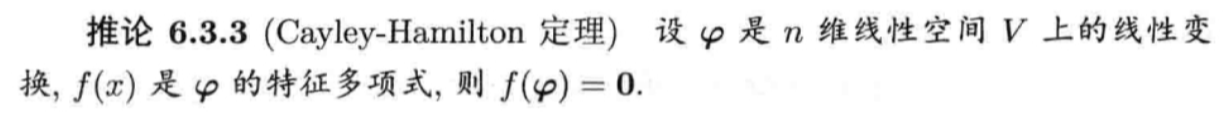
第七章 相似标准型
7.1 多项式矩阵
定义7.1.1 λ-矩阵的初等行变换
定义7.1.2 λ-矩阵相抵
定义7.1.3 初等λ-矩阵
定理7.1.1 对λ-矩阵A(λ)施行第k类初等行(列)变换 等价于 用第k类初等λ-矩阵左乘(右乘)A(λ)。
定义7.1.4 逆λ-矩阵,可逆λ-矩阵 | 可逆阵
* 什么是矩阵多项式? *
引理7.1.1 矩阵多项式的带余除法
定理7.1.2 A与B相似 等价于 λI-A与λI-B相抵。
证明:反复利用引理7.1.1以及λ的系数比较。
7.2 矩阵的法式
引理7.2.1 A(λ)相似于B(λ):b_11(λ)≠0且b_11(λ)可整除B(λ)中的任一元素。
证明:对A的元素的deg最小值做数学归纳法,反复利用带余除法。
定理7.2.1 A(λ)相抵于对角阵diag{d_1(λ),...,d_r(λ);0,...,0},其中d_1(λ)是非零首一多项式且d_i(λ)整除d_(i+1)(λ)。
证明:对n用数学归纳法,利用分块矩阵乘法。
* r是A(λ)的秩,但是满秩方阵不一定可逆。 *
* diag{d_1(λ),...,d_r(λ);0,...,0}称为A(λ)的法式或相抵标准型。 *
推论7.2.1 任意n阶可逆λ-矩阵都可表示为有限个初等λ-矩阵的积。
证明:把定理7.2.1的形式写出来,讨论得r=n,……。
推论7.2.2 A的特征矩阵λI-A必相抵于diag{1,...,1,d_1(λ),...,d_m(λ)},其中d_i(λ)整除d_(i+1)(λ)。
证明:把定理7.2.1的形式写出来,讨论得r=n,……。
7.3 不变因子
定义7.3.1 k阶行列式因子
引理7.3.1 非零行列式因子依次满足整除关系。
证明:把i+1阶子式展开即可。
定义7.3.2 不变因子
定理7.3.1 相抵的λ-矩阵有相同的行列式因子,从而有相同的不变因子。
证明:只要证明行列式因子在任意一种初等变换下不变即可。
推论7.3.1 A(λ)的法式为diag{d_1(λ),...,d_r(λ);0,...,0},则其不变因子为d_1(λ),...,d_r(λ)。
证明:A(λ)与diag{d_1(λ),...,d_r(λ);0,...,0}相抵,从而有相同的不变因子。
推论7.3.2 A(λ)与B(λ)相抵当且仅当它们有相同的法式。
推论7.3.3 A(λ)的法式与初等变换的选取无关。
* λI-A的行列式因子与不变因子均简称为A的行列式因子与不变因子。 *
推论7.3.4 设F⊆K是两个数域,A,B是F上的两个矩阵,则A和B在F上相似的充分必要条件是它们在K上相似。
7.4 有理标准型
引理7.4.1

证明:(2)利用e_1,e_1*F,...,e_1*F^(r-1)线性无关即得。
引理7.4.2

定理7.4.1

定义7.4.1 矩阵A的有理标准型或Frobenius标准型;Frobenius块
定理7.4.2 极小多项式m(λ)等于次数最高的不变因子。
7.5 初等因子
定义7.5.1 初等因子,初等因子组
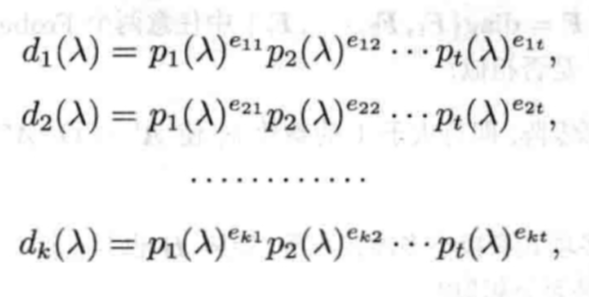
定理7.5.1 初等因子组是相似关系的全系不变量。
证明:初等因子he行列式因子可以互相确定。
7.6 Jordan标准型
引理7.6.1

引理7.6.2

引理7.6.3


定理7.6.1

定义7.6.1 Jordan标准型,Jordan块
定理7.6.2

推论7.6.1

推论7.6.2

推论7.6.3

推论7.6.4

推论7.6.5

7.7 Jordan标准型的进一步讨论和应用
定理7.7.1

定义7.7.1

定义7.7.2

定理7.7.2

引理7.7.1

定理7.7.3

7.8 矩阵函数


定义 矩阵序列收敛 / 发散,矩阵级数收敛 / 发散,矩阵幂级数
定理7.8.1

定理7.8.2


* 在具体计算矩阵函数时不要随便套用数值函数的性质。 *

