计算机图形学之光栅图形学算法
计算机图形学概论
基本概念
1、一般来说要在计算机上生成一幅表示物体的图像有三步:造型技术;光照模型;绘制(渲染)技术
2、帧缓冲器
3、分辨率:屏幕分辨率;显示分辨率;显卡分辨率
4、显示器点距(越小越好,一般14或15寸电脑显示器点距为0.27mm)
5、图形与图像的区别
6、位图(点阵图)和矢量图的区别:1)存储方式的区别:点阵文件是存储图的各个像素点的位置信息、颜色信息以及灰度信息。矢量文件通常用图形的形状参数和属性参数来表示图形。2)缩放的区别:位图与分辨率有关而矢量图与分辨率无关。3)存储格式的区别。
7、计算机图形系统的组成:输入,存储,交互,计算,输出
简单计算
1、显示颜色为64K,分辨率为1024*1024,至少需要的帧缓存容量为:2M
光栅图形学算法
光栅图形算法多数属于计算机图形的底层算法,很多图形学的基本概念和思想都在这一部分。研究内容主要有:
~直线段的扫描转换算法
~多边形的扫描转换与区域填充算法
~裁剪算法
~反走样算法
~消隐算法
一、直线段的扫描转换算法
直线是最基本的图形,一个动画或真实感图形往往需要调用成千上万次画线程序,因此直线算法的好坏与效率将直接影响图形的质量和显示速度。在数学上,直线上有无穷多个点。但在计算机光栅显示器上需要用有限个像素点去无限逼近这无穷多个点,因此就需要知道这些像素点的x,y坐标。
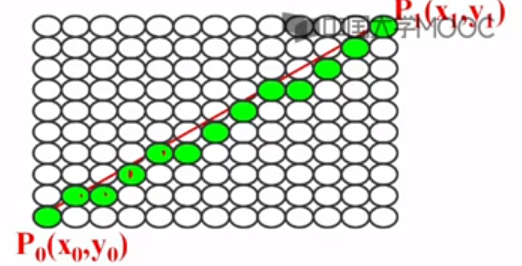
1、DDA画线算法
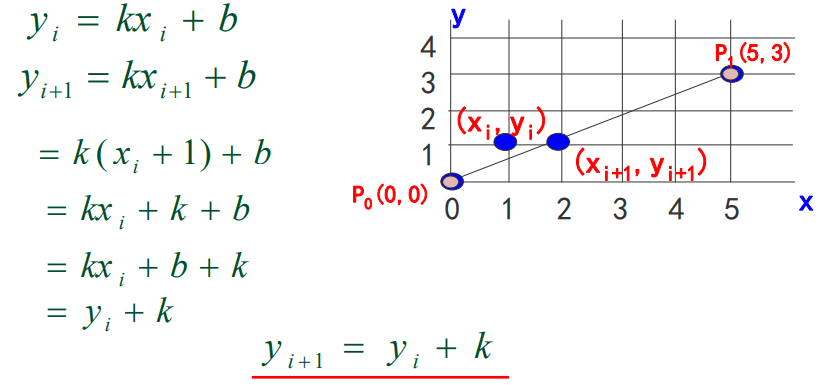
在确定像素点位置时可以利用直线方程 y = kx + b , 根据x点的坐标得到y点的坐标,但是这样计算会使用到乘法,若是能将乘法运算转换成加法运算,效率就会提高。数值微分DDA(Digital Differential Analyzer)法引进图形学中一个很重要的思想——增量思想。
假设x0已知,每次沿x轴方向前进一个像素(步长为1),可以计算出相应的y值。因为像素点的坐标为整数,所以还要将计算得到的y值进行取整处理,取整的方法是将其加0.5再取整。如下推论可以得到增量公式,它的含义是当前y值等于前一步的y值加上斜率k,k称为增量。
2、中点画线算法
中点画线算法不使用直线的斜截式方程,而使用直线的一般式方程F(x, y) = Ax + By + C 。一条直线将平面划分为三个部分:直线上的点、直线上方的点和直线下方的点。中点画线算法每次在x方向上的步长为1,而在y方向上要不要变化需要判断。其中判断方法是取Pu和Pd的中点M,判断M点在Q点的上方还是下方。若M点在Q点的下方,说明Pu点距离直线更近,所以选择Pu点;若M点在Q点的上方,说明Pd点距离直线更近,所以选择Pd点;若M点正好位于Q点处,则选择Pu和Pd都可以。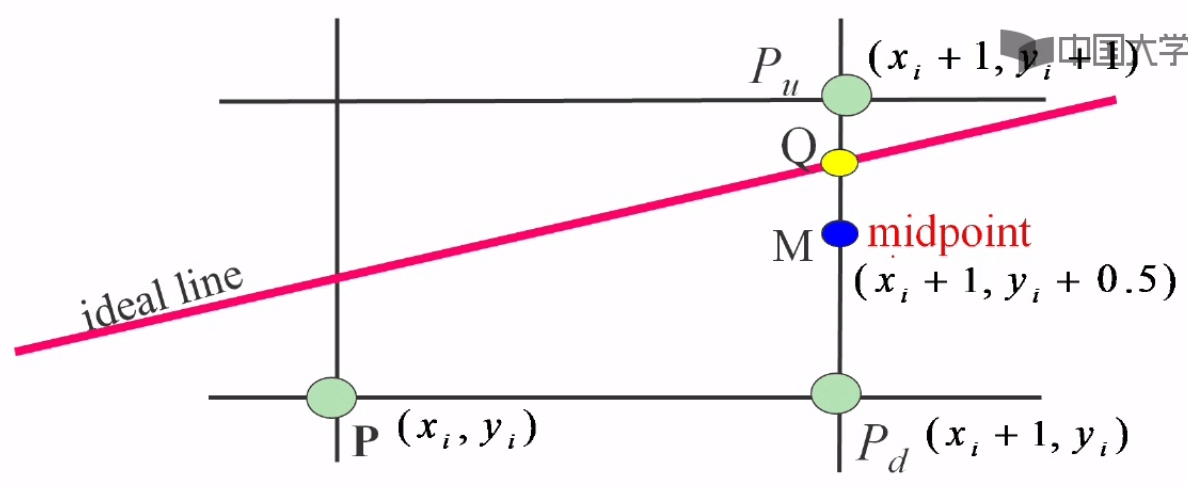
根据以上算法很容易知道要求的下一个像素点的坐标需要进行一次乘法运算和四次加法运算:di = A(Xi + 1) + B(Yi + 0.5) + C,其效率是很低的,因此这里也引入增量的思想求di。
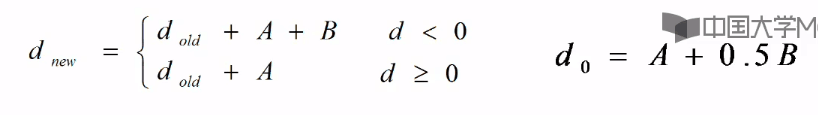
3、Bresenham算法
Bresenham算法并不依赖于直线方程,它提供了一个更一般的算法,该算法不仅有好的效率,而且有更广泛的适用范围。该算法的基本思想是通过各行、各列像素中心构造一组虚拟的网格线,按照直线起点到终点的顺序,计算直线与各垂直网格线的交点,然后根据误差项的符号确定该像素中与此交点最近的像素。该算法中增量 d = k ,且当d > 1时就将其减一,以保证算法的连续性。

将Bresenham算法进行一些改进:
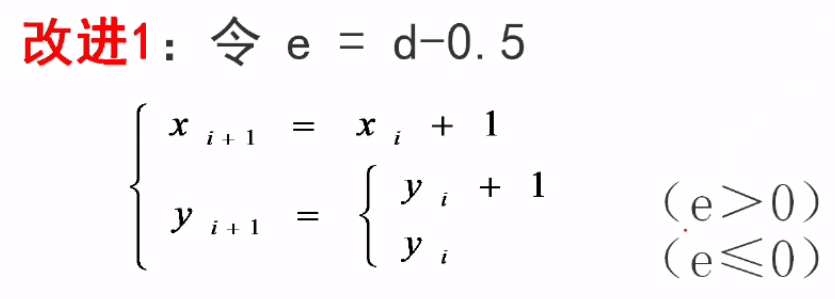

二、多边形扫描转换与区域填充
多边形分为凸多边形(任意两顶点间的连线均在多边形内)、凹多边形(任意两顶点间的连线有不在多边形内的)和含内环的多边形等。多边形的扫描转换和区域填充是研究怎么样在离散的像素集上表示一个连续的二维图形。多边形有两种表示方法:顶点表示(表示直观、几何意义强、占内存少,易于进行几何转换,但不能直接用于面着色)和点阵表示(丢失很多信息,但却是光栅显示系统显示时所需的表现形式)。这就涉及到了两个问题:1、如果知道边界,能否求出哪些像素在多边形内;2、知道多边形内部的像素,反过来如何求多边形的边界。计算机图形学解决的是第一个问题,这种转换称为多边形的扫描转换。
1、X—扫描线算法
X—扫描线算法的基本思想是按扫描线的顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。算法步骤如下:
1)确定多边形所占有的最大扫描线数,得到多边形顶点的最小和最大y值(ymin和ymax);
2)从 y = ymin 到 y = ymax,每次用一条扫描线进行填充;
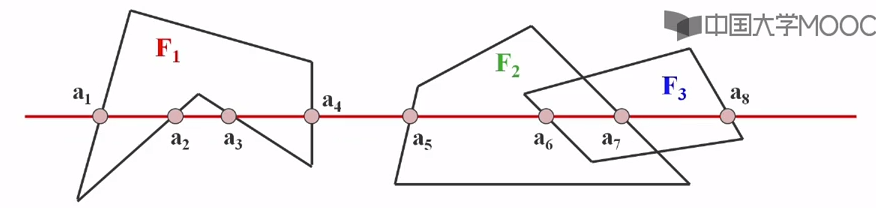
3)对每一条扫描线填充的过程可分为四个步骤:a、求交:计算扫描线与多边形各边的交点;b、排序:把所有交点按递增顺序进行排序;c、交点配对(要保证扫描线与多边形的交点是偶数个):第一个与第二个,第三个与第四个;d、区间填色:把这些相交区间内的像素置成不同与背景色的填充色。当扫描线与多边形顶点相交时,要考虑交点的取舍问题。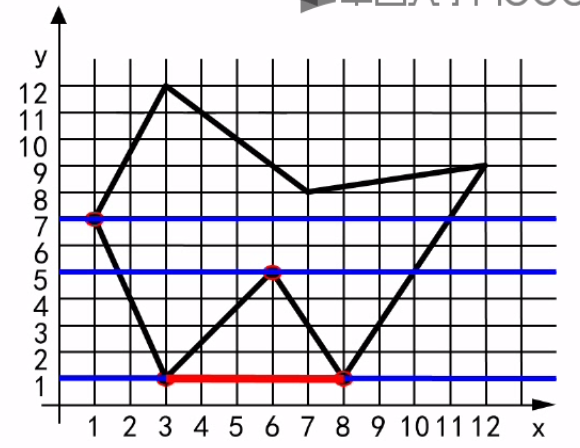
解决方案:若共享顶点的两条边分别落在扫描线的两边,交点只能算一个;若共享顶点的两条边在扫描线的同一边,这时交点作为零或两个,检查共享顶点的两条边的两外两个端点的y值,按这两个y值中大于交点y值的个数来决定交点数。如上图:点(1,7)交点算一个;点(3,1)和点(8,1)算两个;点(6,5)算零个。
以上的算法效率非常低,因为需要大量的求交运算,而求交运算是非常可怕的。
因此需要对以上算法进行改进,想办法不进行求交运算。可以从以下三个方面考虑加以改进:
1)在处理一条扫描线时,仅对与它相交的多边形的边(有效边)进行求交运算。下图中有效边为:P1P4和P2P3

2)考虑扫描线的连贯性,即当前扫描线与各边的交点顺序与下一条扫描线与各边的交点顺序可能相同或非常相似。
3)最后考虑多边形的连贯性,即当某条边y与当前扫描线相交时,它很可能也与下一条扫描线相交。为了避免求交运算,我们需要引进一套数据结构
该数据结构包括以下几个部分:
1)活性边表(AET):把当前与扫描线相交的边称为活性边,并把他们按照与扫描线交点x坐标递增的顺序存放在一个链表中。
2)结点内容:x(当前扫描线与边交点的横坐标),▲x(从当前扫描线到下一条扫描线间x的增量),ymax(该条边上最大的y值,通过它判断该条线还是不是活性边)。容易知道▲x的值为1/k,其中k为直线斜率。
为了方便活性边表的建立与更新,还需要构造一个新边表(NET),用来存放多边形的边的信息,分为四个步骤:
1)首先构造一个纵向链表,链表的长度为多边形所占有的最大扫描线数,链表的每个结点,称为一个吊桶,对应多边形覆盖的每一条扫描线。、
2)NET挂在与该边低端y值相同的扫描线桶中。结点中包含的信息有:该边的ymax、该边较低点的x坐标值xmin、1/k以及指向下个结点的指针。
2、区域填充算法
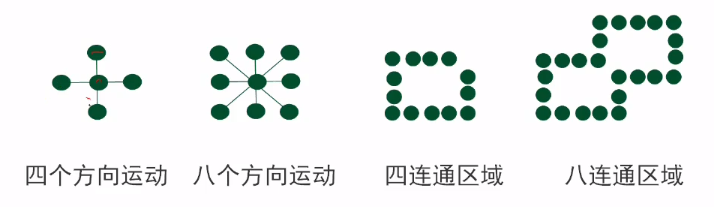
区域是指已经表示成点阵形式的填充图形,是象素的集合。区域填充是指将区域内的一点(常称种子点)赋予给定的颜色,然后将这种颜色扩展到整个区域的过程。区域填充算法要求区域是联通的,因为只有在联通的区域中,才能将种子点的颜色扩展到区域内的其他点,区域可以分为4向联通区域和8向联通区域
算法步骤:将种子象素入栈,当栈非空时重复执行如下的三个步骤
1)栈顶象素出栈
2)将出栈象素置成要填充的颜色
3)按左、上、右、下的顺序检查与栈象素相邻的四个象素,若其中某个象素不在边界且没有置成填充色,则把该象素入栈。
三、反走样
解决走样的方法:非加权区域采样法、加权区域采样法
非加权区域采样法:根据物体的覆盖率计算象素的颜色。覆盖率是指某个象素区域被物体覆盖的比例。、
四、消隐算法
要消除二义性,就必须在绘制时消除被遮挡的不可见的线或面,习惯上称作消除隐藏线和隐藏面,简称为消隐。消隐不仅与消隐对象有关,还与观察者的位置有关。消隐一般分为两大类,按照消隐对象分类可以分为线消隐(消隐对象是物体的边)和面消隐(消隐对象是物体上的面);按消隐空间可以分为物体空间的消隐算法和图像空间的消隐算法。以下是三个基于图像空间的消隐算法:
1、Z-buffer算法:也叫深度缓冲器算法,该算法有帧缓冲器和深度缓冲器,对应两个数组。
Intensity(x, y)——属性数组,存储图像空间的每个可见象素的光强或颜色;
Depth(x, y)——深度数组,存放图像空间每个可见象素的z坐标。
算法步骤:
1)先将Z缓冲器中的各单元的初始值置为最小值;
2)当要改变某个象素的颜色值时,首先检擦当前多边形的深度值是否大于该象素原来的深度值;
3)如果大于原来的Z值,说明当前多边形更靠近观察者,用它的颜色替换象素原来的颜色。
判断一个像素点是否在多边形内部的方法:射线法、弧长法和以顶点符号为基础的弧长累加方法
2、区间扫描线算法:扫描线的交点把这条扫描线分成了若干个区间,每个区间上必是同一种颜色。
如何确定小区间的颜色:
1)小区间上没有任何多边形,则用背景色显示;
2)小区间只有一个多边形,则显示该多边形的颜色;
3)小区间上存在两个或两个以上的多边形,必须通过深度测试判断哪个多边形可见
3、Warnock消隐算法(区域子分割算法):把物体投影到全屏幕窗口上,然后递归分割窗口,直到窗口内目标足够简单,可以显示为止。
1)如果窗口内没有物体则按背景色显示;
2)如果窗口内只有一个面,则把这个面显示出来;
3)否则,窗口内含有两个以上的面,则把窗口等分为四个子窗口。对每个子窗口再做上述同样的处理。这样反复的进行下去。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号