[HihoCoder-1185] 连通性·三 【tarjan+缩点】
题面：
描述
暑假到了!!小Hi和小Ho为了体验生活，来到了住在大草原的约翰家。今天一大早，约翰因为有事要出去，就拜托小Hi和小Ho忙帮放牧。
约翰家一共有N个草场，每个草场有容量为W[i]的牧草，N个草场之间有M条单向的路径。
小Hi和小Ho需要将牛羊群赶到草场上，当他们吃完一个草场牧草后，继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后，小hi和小Ho就把牛羊群赶回家。
一开始小Hi和小Ho在1号草场，在回家之前，牛羊群最多能吃掉多少牧草？
举个例子：
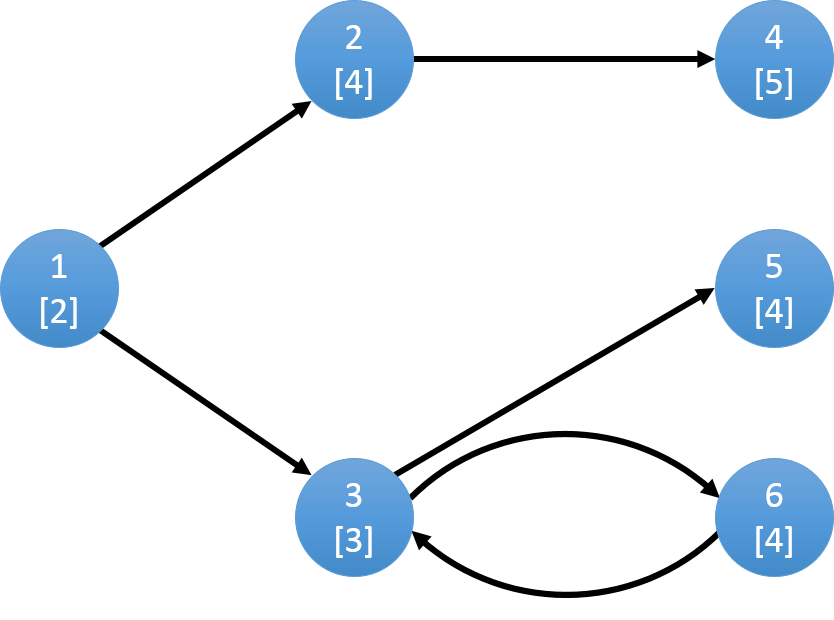
图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。
在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：
吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3，则可以到达5，6：
选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。
所以该图可以选择的路线有3条：
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5: total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示：强连通分量
输入
第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行：1个整数，最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
大致思路：
这个题需要一个缩点的操作，也就是说在基础的tarjan算法上，需要加一个数组（程序中是sccno），其意义是：如果存在连通分量，则sccno[i]的值是这个树的根节点，也就是可以通过这个数组知道属于哪个联通分量。
所以整个题的过程就是先跑一遍tarjan，然后根据sccno的信息新建一个图，然后再新建的图上跑一遍dfs，最后扫一遍glass数组，求一个max输出就可以了。
代码：
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=2e4+7; 4 vector<int> g[maxn]; 5 vector<int> newp[maxn]; 6 int dfn[maxn],low[maxn],w[maxn],glass[maxn],sccno[maxn]; 7 int idx=0; 8 bool visit[maxn]; 9 stack<int> s; 10 void tarjan(int u) 11 { 12 dfn[u]=low[u]=++idx; 13 s.push(u); 14 visit[u]=true; 15 int v; 16 for(int i=0;i<g[u].size();++i){ 17 v=g[u][i]; 18 if(dfn[v]==0){ 19 tarjan(v); 20 low[u]=min(low[u],low[v]); 21 }else if(visit[v]) 22 low[u]=min(low[u],dfn[v]); 23 } 24 if(dfn[u]==low[u]) 25 do{ 26 v=s.top(); 27 s.pop(); 28 sccno[v]=u;//指向根节点 29 visit[v]=false; 30 }while(u!=v); 31 } 32 33 void suodian(int n) 34 { 35 int v,u; 36 for(int i=1;i<=n;++i){ 37 for(int j=0;j<g[i].size();++j){ 38 u=g[i][j]; 39 if(sccno[i]==u) 40 continue; 41 if(w[u]==0) 42 continue; 43 if(u!=sccno[u]){ 44 w[sccno[u]]+=w[u];//缩点时将值累加 45 w[u]=0; 46 }else 47 newp[sccno[i]].push_back(u);//为了让连通分量连接的边成功接上根节点 48 } 49 } 50 } 51 void dfs(int x,int last) 52 { 53 int v; 54 glass[x]=max(glass[x],glass[last]+w[x]); 55 for(int i=0;i<newp[x].size();++i){ 56 v=newp[x][i]; 57 if(w[v]!=0&&visit[v]==false){ 58 visit[v]=true; 59 dfs(v,x); 60 visit[v]=false; 61 } 62 } 63 } 64 65 int main() 66 { 67 ios::sync_with_stdio(false); 68 //freopen("in.txt","r",stdin); 69 int n,m,u,v; 70 memset(dfn,0,sizeof(dfn)); 71 memset(glass,0,sizeof(glass)); 72 cin>>n>>m; 73 for(int i=1;i<=n;++i) 74 cin>>w[i]; 75 for(int i=1;i<=m;++i){ 76 cin>>u>>v; 77 g[u].push_back(v); 78 } 79 for(int i=1;i<=n;++i) 80 sccno[i]=i; 81 tarjan(1); 82 for(int i=1;i<=n;++i) 83 if(dfn[i]==0) 84 w[i]=0; 85 suodian(n); 86 int ans=0; 87 memset(visit,false,sizeof(visit)); 88 visit[1]=true; 89 dfs(1,1); 90 for(int i=1;i<=n;++i) 91 ans=max(ans,glass[i]); 92 cout<<ans<<endl; 93 return 0; 94 }
