计算机图形学复习(一)
图形显示设备
阴极射线管(CRT)
利用磁场产生告诉的、经过聚焦的电子书,偏转到屏幕的不同位置,轰击屏幕表面的荧光材料,从而产生图形。
CRT主要由:电子枪、偏转系统及荧光屏三个基本部分组成。
电子枪:
-
足够的电流强度。为了使光点达到一定亮度。
-
电流的大小和有无必须是可控的。
-
具有很高的速度,才能使荧光粉发出相当的光亮
-
在荧光屏上应能聚焦很小的光亮
偏转系统:
磁偏转系统利用磁场使电子书产生偏转,扫描荧光屏产生字符或图形,这种方式会造成光栅的枕型失真。
矫正措施:
1. 使产生偏转磁场的锯齿形电流预先产生一些失真
2. 故意将偏转磁场做成略有不均匀性,此时光栅将有桶形失真的倾向。从而抵消枕形失真。
荧光屏
对于荧光粉的要求是:发光颜色满足标准白色,发光效率高,余晖时间合适,寿命长等
基本图形生成算法
直线的扫描转换
DDA数值微分法:
给定直线的两端点,$P_0(X_0,Y_0) $ 和 $ P_1(X_1,Y_1) $ 得到直线的微分方程:
原理:
对于当前位置\((x_i,y_i)\) 分别加上两个小增量 $\xi · \Delta x $ 和 \(\xi · \Delta y \) ,就可以求出下一个点的坐标。 既有:
对于增量的取值为:
在绘图时的取值时遇到浮点数采用四舍五入的方法。但之后的计算依然按浮点数而不是四舍五入后的整数。
void DDALine(int x0,int y0,int x1,int y1,int color)
{
int x;
float dx,dy,y,k;
dx=x1-x0;
dy=y1-y0;
k=dy/dx;
y=y0;
for(x=x0;x<=x1;x++)
{
putpixel(x,int(y+0.5),color);//(1)
y=y+k;
}
}
中点 Bresenham
中点算法关键在于它的名字——中点。上下两个像素点连线的中心就是中点,直线在经过像素点的连线的时候形成的交点就是实际的点,只需要判断这个实际点在”中点“的上方还是下方,如果在上方那么取上面的像素点,如果在下方就取下方的像素点。
void MindpointLine(int x0,int y0,int x1,int y1,int color)
{
int a,b,d1,d2,d,x,y;
b=x1-x0;
a=y0-y1;
d=2*a+b;
d1=2*a;
d2=2*(a+b);
x=x0;
y=y0;
putpixel(x,y,color);
while(x<x1)
{
if(d<0)
{x++,y++,d+=d2;}
else
{x++,d+=d1;}
putpixel(x,y,color);
}
}
Bresenham
Bresenham算法也是一种计算机图形学中常见的绘制直线的算法,其本质思想也是步进的思想,但由于避免了浮点运算,相当于DDA算法的一种改进算法。
首先算出斜率, 当 $ |K| \leq 1 $ 时,$ x$ 为主要步进方向 , 当 $ |K| > 1 $ 时, $ y $ 为主要步进方向。
下图是以 $ x $为步进方向的例子:
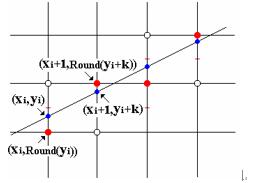
设当前坐标为: $ (x_i,y_i)$ ,则 $ x_{i+1} = x_i +1 $ ,$ y_{i+1} = y_i + k $
当前绘制点坐标应该为:
若 $ int(y_i+0.5) = y_i $ 则在 $ (x_i,lower(y_i)) $处绘制
若 $ int(y_i+0.5) = y_i+1 $ 则在 $ (x_i,upper(y_i)) $处绘制
函数 $ lower(int x) $ 的意义为:返回找到最接近的小于 $ x $ 的整数值
函数 $ upper(int x) $ 的意义为:返回找到最接近的大于 $ x $ 的整数值
void IntegerBresenhamline(int x0,int y0,int x1,int y1,int color)
{
int x,y,dx,dy,e,i;
dx=x1-x0;
dy=y1-y0;
e=-dx;
x=x0;
y=y0;
for(i=0;i<=dx;i++)
{
putpixel(x,y,color);
x++;
e=e+2*dy;
if(e>=0){y++;e=e-2*dx;}
}
}
圆的扫描转换
中点Bresenham画圆算法
#define SHOW_CONSOLE
#include "graphics.h" // 引用ege图形库
#include<iostream>
#include<stdio.h>
#include<math.h>
const int size_x=640,size_y=480;
const double eps = 1e-6;
void CirclePoint(int x,int y,int color)
{
putpixel(x,y,color); putpixel(y,x,color);
putpixel(-x,y,color); putpixel(-y,x,color);
putpixel(-x,-y,color); putpixel(-y,-x,color);
putpixel(y,-x,color); putpixel(x,-y,color);
}
void MidBresenhamCircle(int r,int color)
{
int dx=0,dy=r,d=1-r;
while(dx<=dy)
{
CirclePoint(dx,dy,color);
if(d<0) d += 2*dx+3;
else{
d += 2*(dx-dy)+5;
dy--;
}
dx++;
}
}
int main()
{
initgraph(size_x,size_y); // 初始化显示一个窗口
MidBresenhamCircle(20,WHITE);
getch(); // 暂停一下等待用户按键
closegraph(); // 关闭图形界面
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号