[笔记]线段树优化建图

Aha

用途

CodeForces一道有趣的模板题

用于短时间内完成:

• 点和区间
• 区间和点
• 区间和区间

之间的连边

方法

初始

整俩线段树

我们维护两棵线段树\(A,B\)，其中一棵每一个节点向父亲连代价为\(0\)的边，另一棵每一个节点向儿子连代价为\(0\)的边。再把对应的叶子节点之间相连(在建图的时候可以直接使叶子节点标号相同)

然后你是不是已经会了

放上丑丑的代码qwq

	int BUILD(int l,int r,int pd){
		if(l==r)return l;
		int x=++tot;
		int mid=(l+r)>>1;
		son[x][0]=BUILD(l,mid,pd);
		son[x][1]=BUILD(mid+1,r,pd);
		if(pd==0)rep(i,0,1)ADD(son[x][i],x,0);
		else rep(i,0,1)ADD(x,son[x][i],0);
		return x;
	}

连边

点——区间：点\(u\)向\([l,r]\)的每个点连代价为\(w\)的边

蓝色的是目标区间，粉红色的是线段树区间查询时完全被覆盖的点

那么点向区间连边，只需要把点和\(A\)树上对于的区间之间连一条代价为\(w\)的边，就可以通过线段树上的黑边不花费任何代价走到区间里的每一个点

区间——点：区间\([l,r]\)里的每一个点向点\(u\)连代价为\(w\)的边

同样的道理，只需要从\(B\)树上对应的区间向\(u\)连代价为\(w\)的边，那么区间里的点就可以花费0的代价从黑边走到粉色节点，再花费\(w\)的代价走橙边到\(u\)

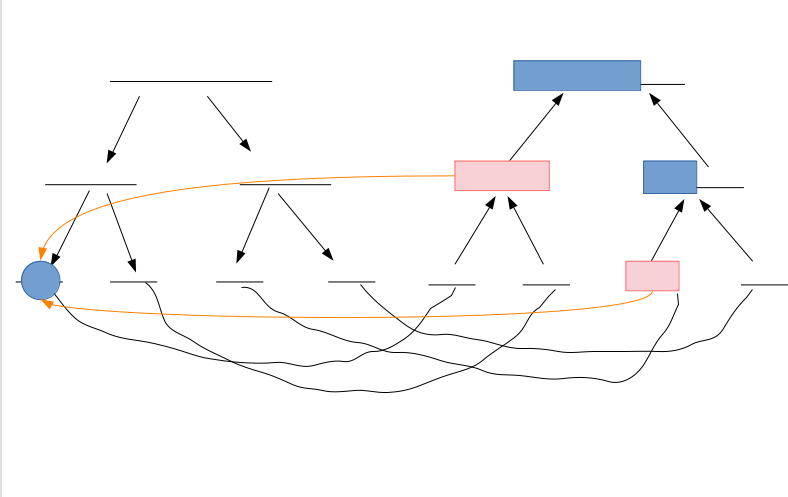
区间——区间：区间\([l_1,r_1]\)向\([l_2,r_2]\)连边

发现区间和区间之间不太好搞哎

我们可以建一个新的节点\(u\),B树上的对应区间向\(u\)连边，\(u\)向A树上的对应区间连边，就转化成了上面的两种情况啦

具体实现的话可以一起写，找到对应节点再特判怎么连边就可以了

void UPD(int x,int l,int r,int la,int ra,int pos,LL val,int pd){
		if(l==la&&r==ra){
			if(pd==2)ADD(pos,x,val);
			else ADD(x,pos,val);//特判
			return;
		}
		int mid=(l+r)>>1;
		if(la>mid)UPD(son[x][1],mid+1,r,la,ra,pos,val,pd);
		else if(ra<=mid)UPD(son[x][0],l,mid,la,ra,pos,val,pd);
		else{
			UPD(son[x][0],l,mid,la,mid,pos,val,pd);
			UPD(son[x][1],mid+1,r,mid+1,ra,pos,val,pd);
		}
	}

求值

最后跑一遍Dijkstra就可以啦

代码

注意：

• 数组要开够
• 最后跑最短路的时候是对所有线段树上的点跑，而不是只对\(n\)个点跑

猴啦放上完整代码

#include<bits/stdc++.h>
#define rep(X,A,B) for(int X=A;X<=B;X++)
#define tep(X,A,B) for(int X=A;X>=B;X--)
#define LL long long
const int N=100010;
const int NN=400010;
const int M=6000010;
using namespace std;

int n,m,S;
int vis[NN];
LL dis[NN],wei[M];
int son[NN][2],tot=0;
int edge[M],lst[NN],nxt[M],t=0;

struct nn{
	int id;
	LL dis;
	
	bool operator < (const nn &A) const {
		return dis > A.dis;
	}
};

priority_queue<nn>Q;

void ADD(int x,int y,LL z){
	edge[++t]=y;nxt[t]=lst[x];lst[x]=t;wei[t]=z;
}

struct SegmentTree{
	int RT;
	
	int BUILD(int l,int r,int pd){
		if(l==r)return l;
		int x=++tot;
		int mid=(l+r)>>1;
		son[x][0]=BUILD(l,mid,pd);
		son[x][1]=BUILD(mid+1,r,pd);
		if(pd==0)rep(i,0,1)ADD(son[x][i],x,0);
		else rep(i,0,1)ADD(x,son[x][i],0);
		return x;
	}

	void UPD(int x,int l,int r,int la,int ra,int pos,LL val,int pd){
		if(l==la&&r==ra){
			if(pd==2)ADD(pos,x,val);
			else ADD(x,pos,val);
			return;
		}
		int mid=(l+r)>>1;
		if(la>mid)UPD(son[x][1],mid+1,r,la,ra,pos,val,pd);
		else if(ra<=mid)UPD(son[x][0],l,mid,la,ra,pos,val,pd);
		else{
			UPD(son[x][0],l,mid,la,mid,pos,val,pd);
			UPD(son[x][1],mid+1,r,mid+1,ra,pos,val,pd);
		}
	}
}ta,tb;

void INIT(){
	scanf("%d%d%d",&n,&m,&S);
	tot=n;
	ta.RT=ta.BUILD(1,n,0);
	tb.RT=tb.BUILD(1,n,1);
}

void SOLVE(){
	int pd,u,v,l,r;
	LL w;
	scanf("%d",&pd);
	if(pd==1){
		scanf("%d%d%lld",&u,&v,&w);
		ADD(u,v,w);
	}
	else{
		scanf("%d%d%d%lld",&u,&l,&r,&w);
		if(pd==2)tb.UPD(tb.RT,1,n,l,r,u,w,pd);
		else ta.UPD(ta.RT,1,n,l,r,u,w,pd);
	}
}

void DIJ(){
	rep(i,1,tot)dis[i]=-1,vis[i]=0;
	dis[S]=0;Q.push((nn){S,0});
	while(!Q.empty()){
		int x=Q.top().id;Q.pop();
		if(vis[x])continue;
		vis[x]=1;
		for(int r=lst[x];r;r=nxt[r]){
			if(dis[edge[r]]!=-1&&dis[edge[r]]<=dis[x]+wei[r])continue;
			dis[edge[r]]=dis[x]+wei[r];
			Q.push((nn){edge[r],dis[edge[r]]});
		}
	}
	rep(i,1,n)printf("%lld ",dis[i]);
}

int main(){
	INIT();
	rep(i,1,m)SOLVE();
	DIJ();
	return 0;
}