02-信息的表示和处理

二进制&十进制&十六进制

二进制转十六进制（分组转换）

四位二进制可表示一位十六进制，那么对于一个0000 1011，转换后的结果为0x0B，只需要记住关键的十六进制和二进制对应关系即可，关系表如下：

对某个二进制如0010 0000 0000，可将其拆分为：\(2^n\) 中 \(n = i + 4j\)，即\(2^9\)进行上述拆分结果为： \(9 = 1 + 4\times2\)，我们需要知道\(i = 0,1,2,3\)分别对应十六进制\(1,2,4,8\)，那么 \(2^9\) 对应0x200，j有多少个决定了后面多少0，i为几，其对应的十六进制值就是几。

再举例\(2^7\)拆分为\(3+4\times1\)，所以十六进制为0x80；\(2^{15}\)拆分为\(3+4\times3\)，十六进制为0x8000。

十进制转十六进制（辗转相除法）

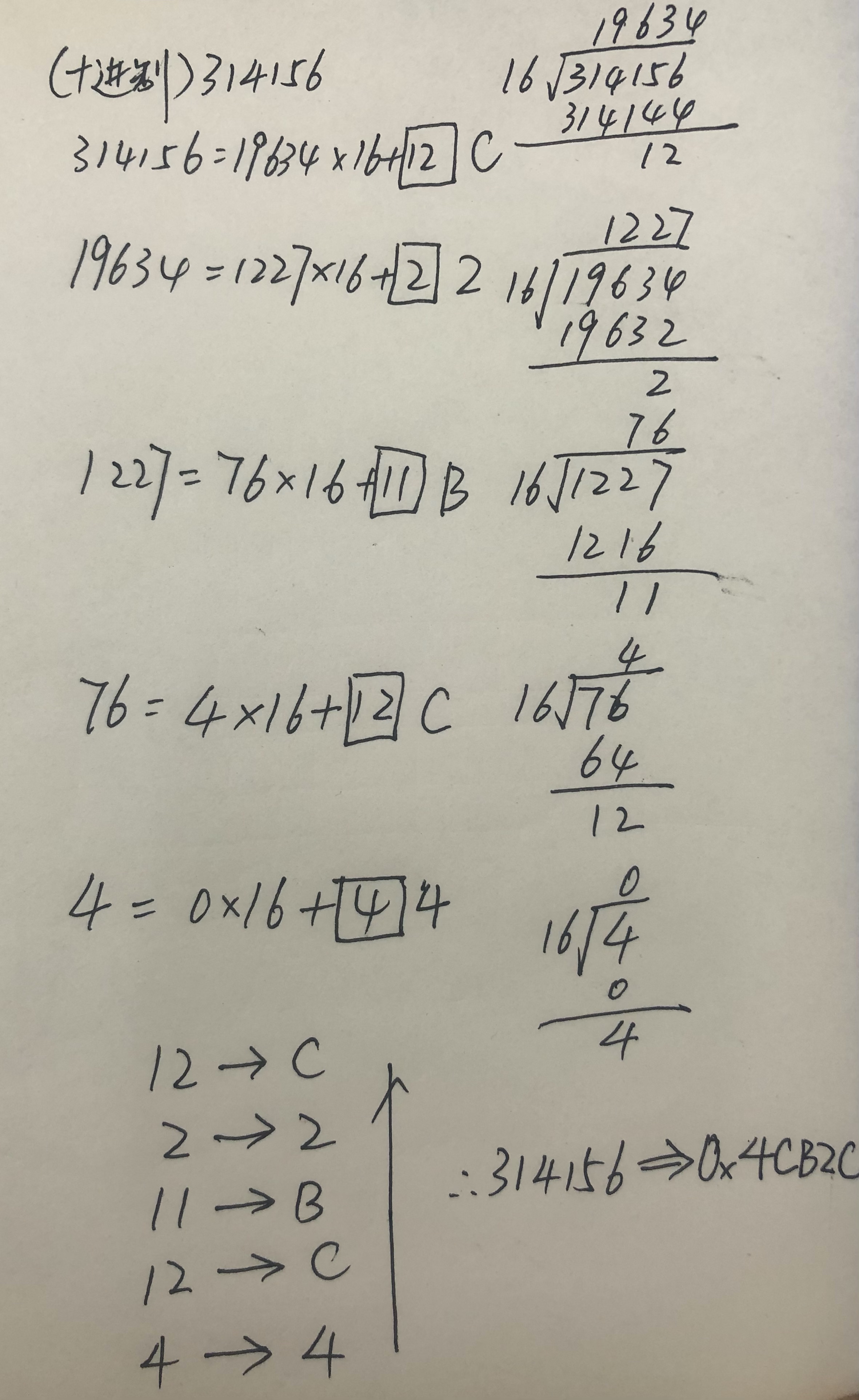
除以16得到的余数逆序转为16进制数，余数由高位到低位排列，314156的十六进制就是0x4CB2C。

十六进制转十进制（直接算）
比如 \(\text{0x7AF} = \text{F}\times 16^0 + \text{A}\times 16^1 + 7\times 16^2 = 1967\)

虚拟地址

虚拟地址实际上是通过内存映射的方式将磁盘物理地址转换得到的地址，在32位字长主机上每个进程能够访问的最大地址空间（虚拟地址空间）大小为4GB，即\(2^{32}\)。

16位字长机器的地址范围：0~65535(FFFF)
32位字长机器的地址范围：0~4294967296（FFFFFFFF,4GB）
64位字长机器的地址范围：0~18446744073709551616（1999999999999998,16EB）
32位编译指令：gcc -m32 main.c
64位编译指令：gcc -m64 main.c

为了避免由于依赖“典型”大小和不同编译器设置带来的奇怪行为，ISOC99引入了类数据类型，其数据大小是固定的，不随编译器和机器设置而变化。其中就有数据类型int32_t和int64_t，它们分别为4个字节和8个字节。使用确定大小的整数类型是程序员准确控制数据表示的最佳途径。

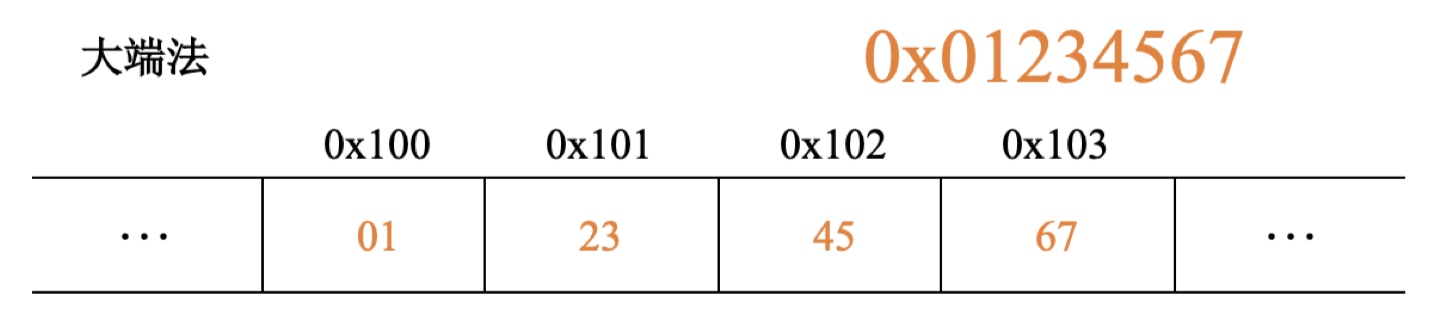
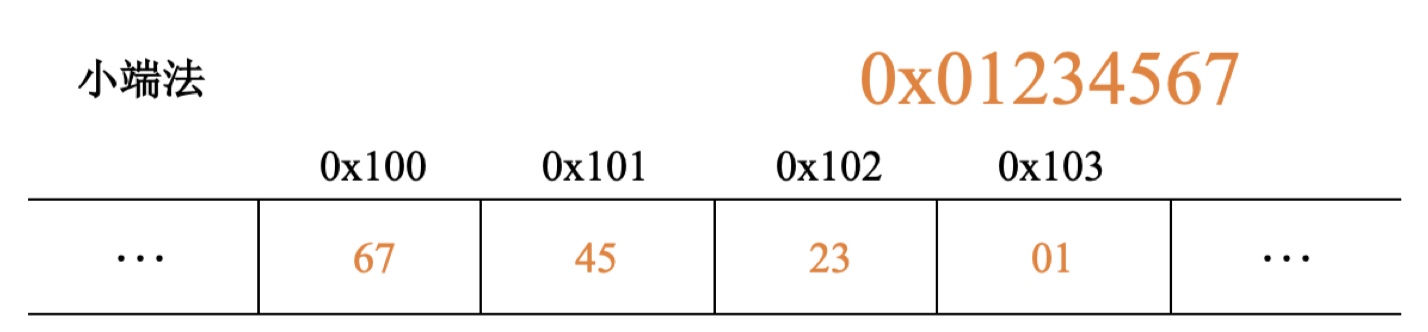
大端小端地址

#include <stdio.h>
int main() {
    unsigned int x = 0x12345678;
    unsigned char *p = (unsigned char *)&x;
    printf("%0x %0x %0x %0x\n", p[0], p[1], p[2], p[3]); //78 56 34 12
    return 0;
}

以上为我的主机测试结果，可以看到低位存储至低地址，这是一个小端的存储方式。

那么为什么要划分大端还是小端地址呢？
我们知道在不同的主机上，会有不同的结果，但是可以明确知道的一点就是，如果两个主机在网络中通信，那么一定是大端方式进行的，这是为了统一字节序的排列而规定的。我们称当前自己的设备上不论大端存储还是小端存储的序列都称为主机字节序，而向网络发送字节序列，我们称之为网络字节序，那么在网络通信中我们需要将主机字节序转换为大端的网络字节序，然后发送到对端接收时再转为其机器的存储方式，即由网络字节序再转为主机字节序，主机字节序有可能是大端或小端，但网络字节序一定是大端存储，这样做的好处是，统一了不同设备存储方式在网络中的字节序列（大端）。

位运算符&逻辑运算符

位运算有：& | ~ ^。逻辑运算（布尔运算）有：&& || !。特别要注意~和!的区别，看下面例子：

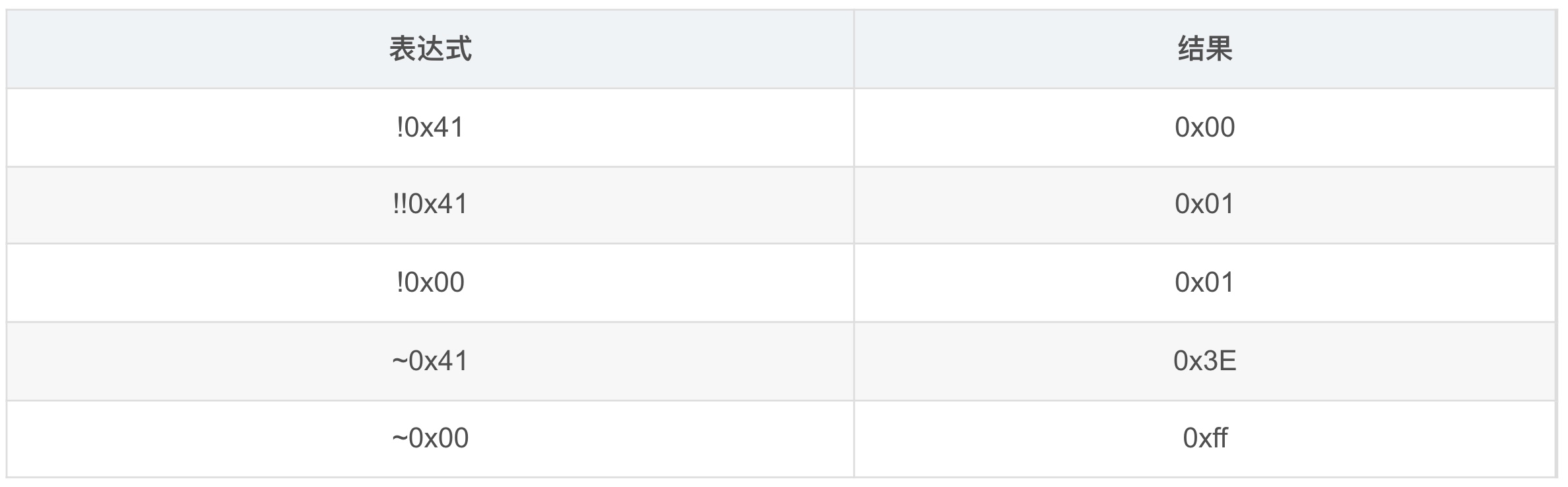
“！”逻辑非运算符，逻辑操作符一般将其操作数视为条件表达式，返回结果为Bool类型：“！true”表示条件为真（true）。“！false ”表示条件为假（false）。"~"位运算符，代表位的取反，对于整形变量，对每一个二进制位进行取反，0变1，1变0。

关于异或^，只需要知道相同为0，相异为1即可。比如0^0=0 0^1=1。

左移&右移

左移直接右侧低位补0，右移的话因为高位可能是符号位的原因，要区分逻辑右移还是算术右移，逻辑右移至的是高位补0，但算术右移高位补符号位。

在计算机中对二进制的数值表示方式有：原码、反码、补码、移码等。原码表示很简单，符号为正则最高位补0，符号为负则最高位补1，我们发现对于0，其原码表示有两种，符号位既可以是1也可是0。原码的表示更易于人为的理解，但计算机对原码的理解就非常困难，特别是计算机进行加减法运算时效率很低，比如两个异号数相加或两个同号数相减时，就要做减法运算，对于ALU运算单元，加法运算时要快于减法运算的，为了减法运算器复杂性，提高运算速度，我们需要把减法运算转换为加法运算，因此人们设计出了反码和补码。

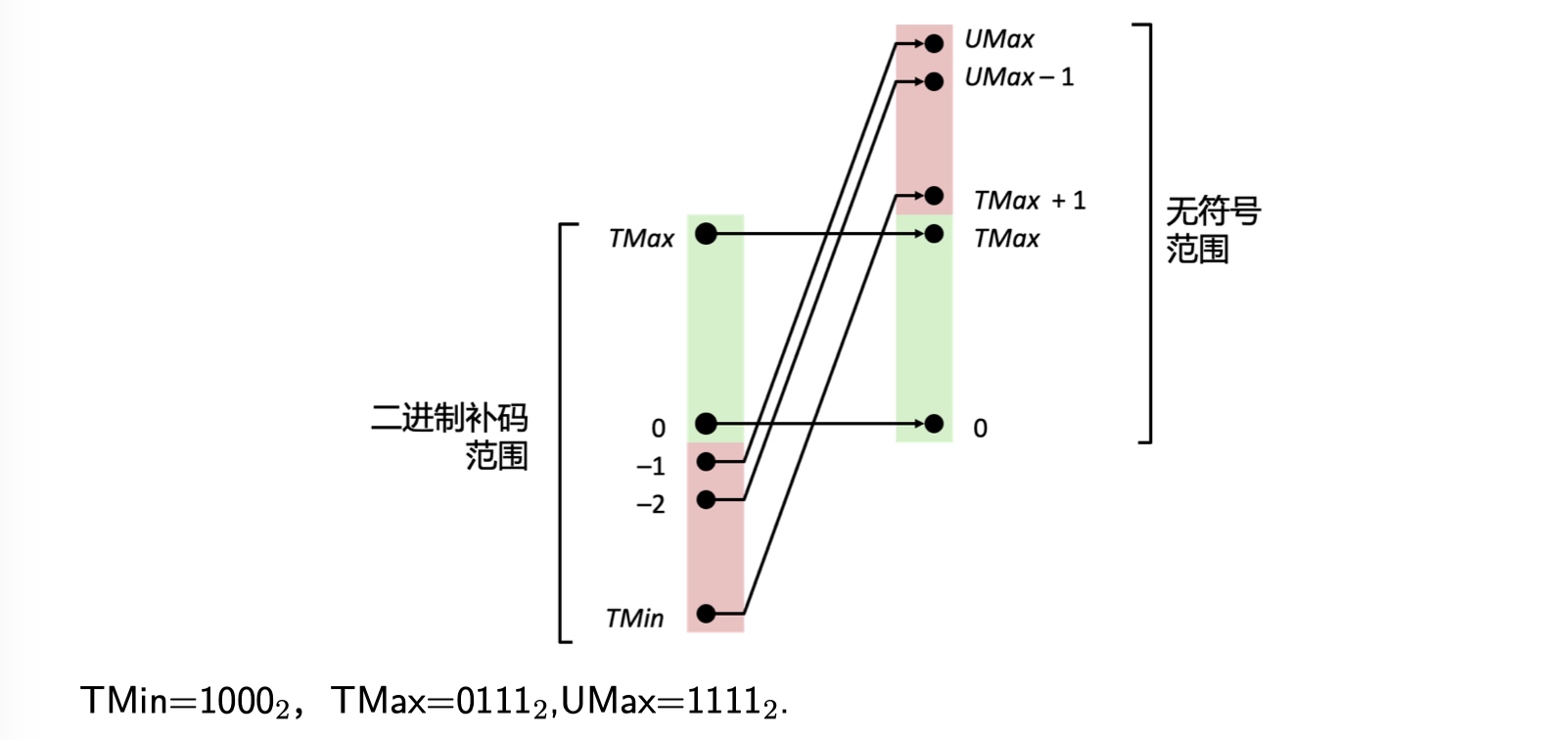
对于原码的表示，若为一个正数，其反码表示不发生改变，若原码数是一个负数，则反码表示需在保持符号位不变的基础上，对其他位按位取反。比如一个正数[X原]=01010110=[X反]，那如果是负数[X原]=10110101，那它的反码就是[X反]=11001010。这种表示有个问题，比如对于0，它在原码中既可以是+0，也可以是-0，即00000000或10000000，那对其进行反码运算，可以看到为两个值00000000或11111111，那对于八位二进制而言我们岂不是表示不了128这个数了，因为0占了两个位置。所以原码和反码的表示范围为：-127~127，为了解决这种情况，才产生了补码。我们将全1的八位二进制作为-128，这个时候0的正确表示就是00000000了，所以补码的表示范围为-128~127。那么以上说的均是对于有符号数而言。

计算机中的运算均是以补码的形式进行的，正数补码与原码一致，与反码也一致。负数的补码需要对原码进行符号位不变，其他位按位取反并+1。或者说我们将最高位作为符号位的同时也作为数值位，就比如如果按照原始方法计算-5，那么其原码为1101，对其求反+1得到结果：1011，所以-5的二进制补码表达为1011，同样我们可以不计算原码而直接得出想要的结果，那最高位1不仅仅是符号，还代表8，所以最高位代表-8，那要得到-5，只需要其他位加起来是3即可，所以-5的补码就是1011，其中第三位011代表3。

二进制补码范围如下图所示，便于理解：

数据类型转换：

• 较小数据类型转较大数据类型（符号扩展）：
  当有符号位数从一个较小的数据类型转换为较大数据类型时，进行符号位扩展可保持数值不变。

• 较大数据类型转较小数据类型：
  高位丢弃，丢弃截断后原值可能会发生改变。

整数计算

无符号数加法：

如，a = 255, b = 1：

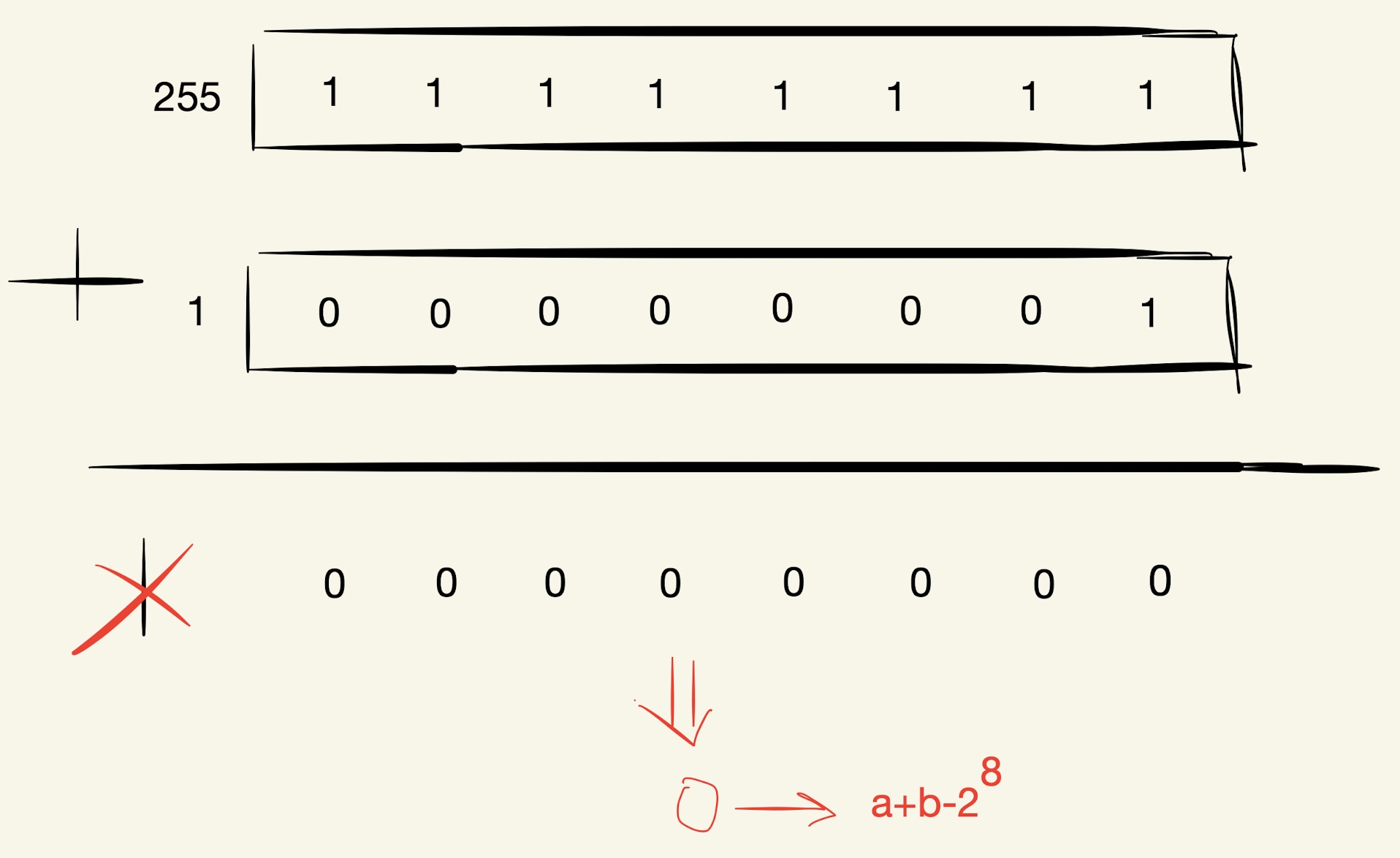
可以看到255+1=0，因为发生了溢出，所以发生溢出的计算公式为\(x+y-2^{\omega}\)，若要预防溢出的情况，一般在代码中实现为：a + b < a && a + b < b，也就是说溢出后的值是比求和前任一值要小的。

有符号数加法（即补码加法）：

我们发现其可能出现正溢出或负溢出，对于正溢出：
若char x=127，char y=1，则计算如下：

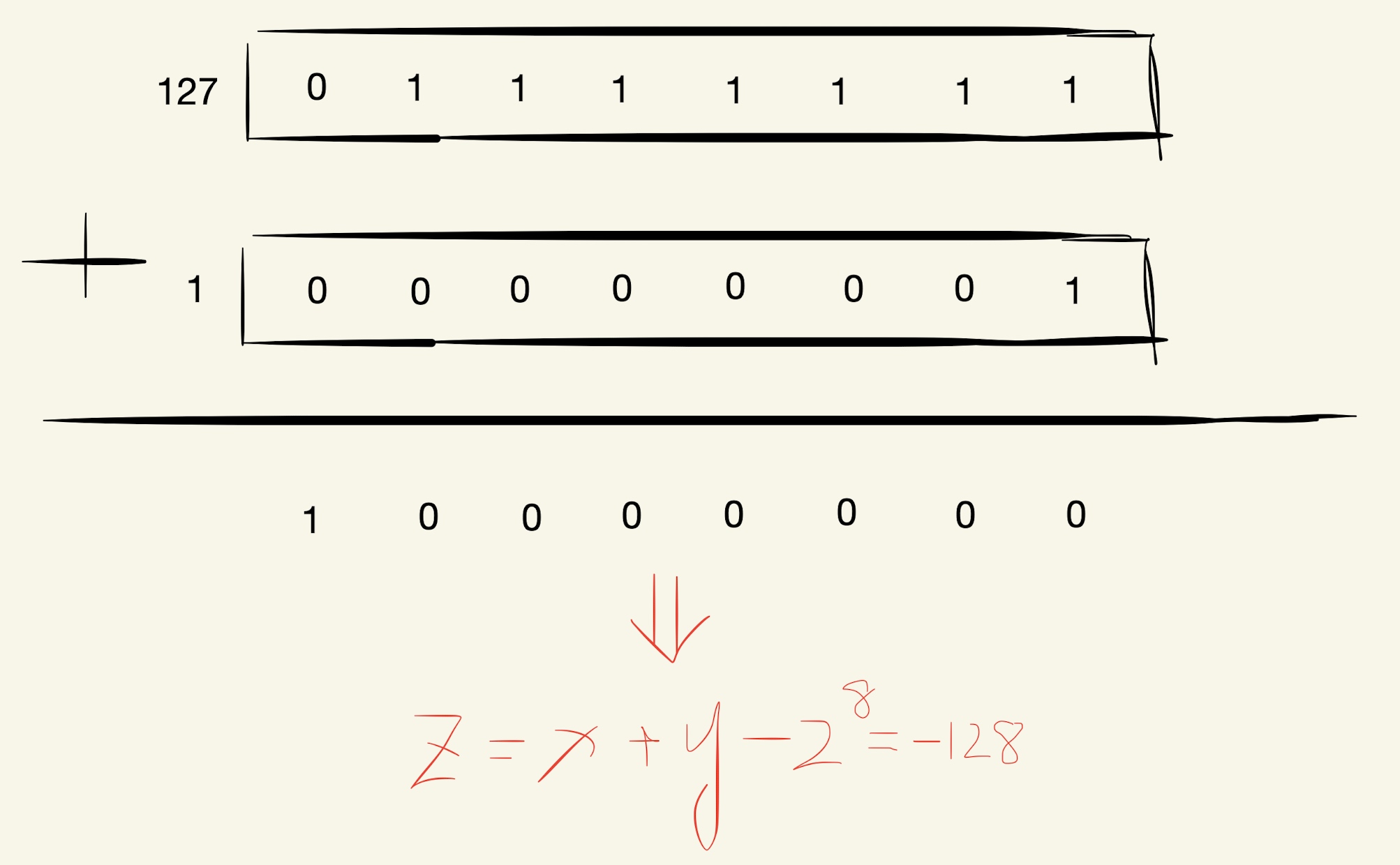
当x=127，y=1时，x+y后高位符号位为1，1000 0000是补码形式，计算结果高位可以是符号位同时也是数值位，所以1000 0000的值为\(-2^7 = -128\)，发生正溢出。

对于负溢出：
若char x=-128，char y=-1，则计算如下：

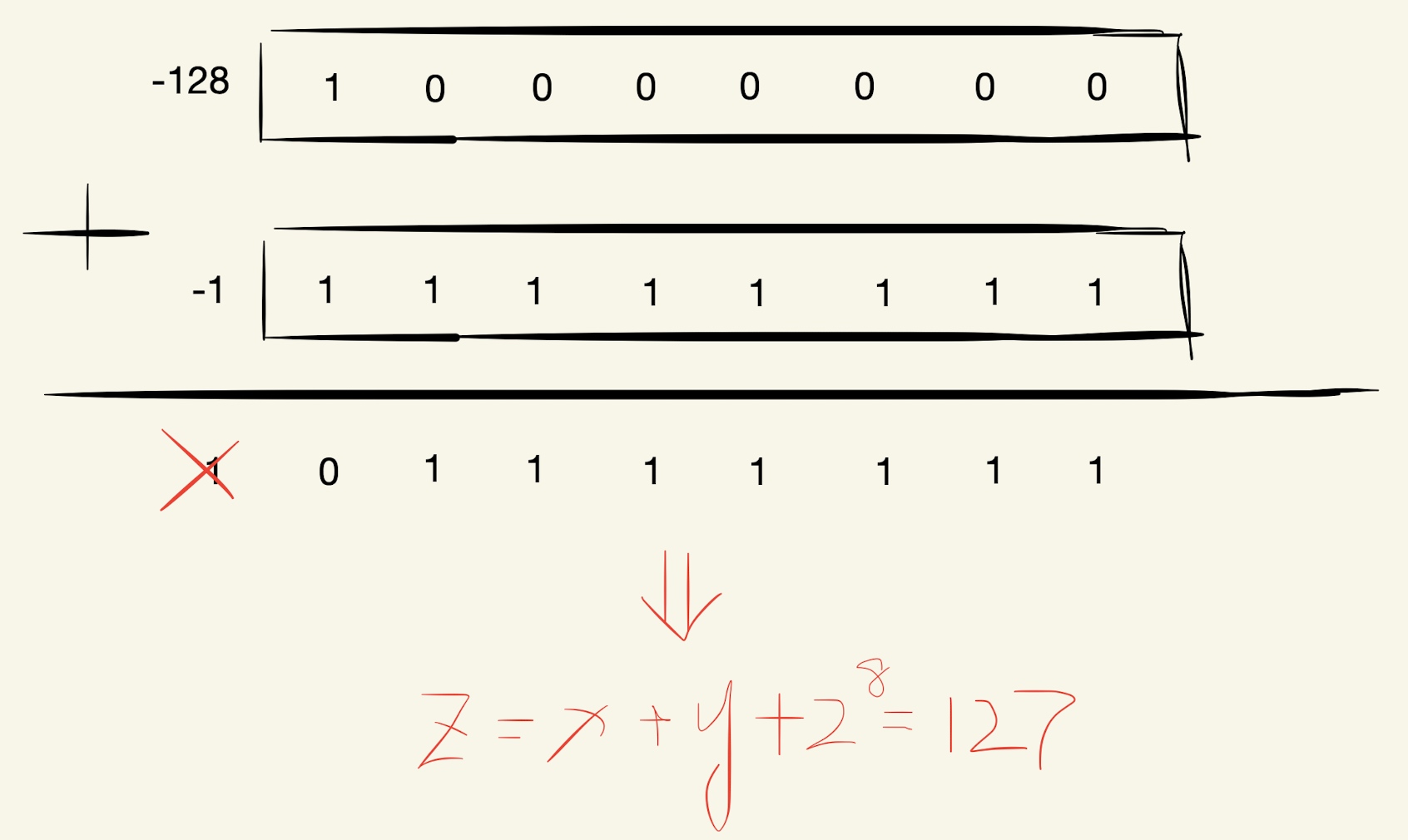
当x=-128，y=-1时，溢出最高位，然后最高位变为0，整体变为正值127，发生了负溢出。

综上可知：
当\(x \geqslant 0, y \geqslant 0, x+y < 0\)，发生正溢出
当\(x \leqslant 0, y \leqslant 0, x+y > 0\)，发生负溢出

对于乘法的相关计算，和加法一样，分为无符号数乘法和有符号数乘法（补码乘法）：

无符号数乘法结果要对其进行取模操作，取模相当于是截断只保留低位，比如下图中3位无符号数x和y，二者的乘积可能需要6位二进制数来表示，那么在C语言中定义了无符号数乘法所产生的结果是3位，因此运行下图得到的\(x\times y\)结果会截取5位中的低3位。截断采用取模的方式，因此运行结果等于x与y乘积并对\(2^3\)取模。

对于无符号的乘2和除以2，我们可以对其进行<<和>>操作执行，左移代表乘以2，右移代表除以2。一般在我们的计算机中，CPU中的ALU只支持加减法运算和移位运算，因此我们不能使用乘法运算法则去进行运算，计算机会将其拆解开来，比如x*14，就可以拆解成如下移位和加法的组合：

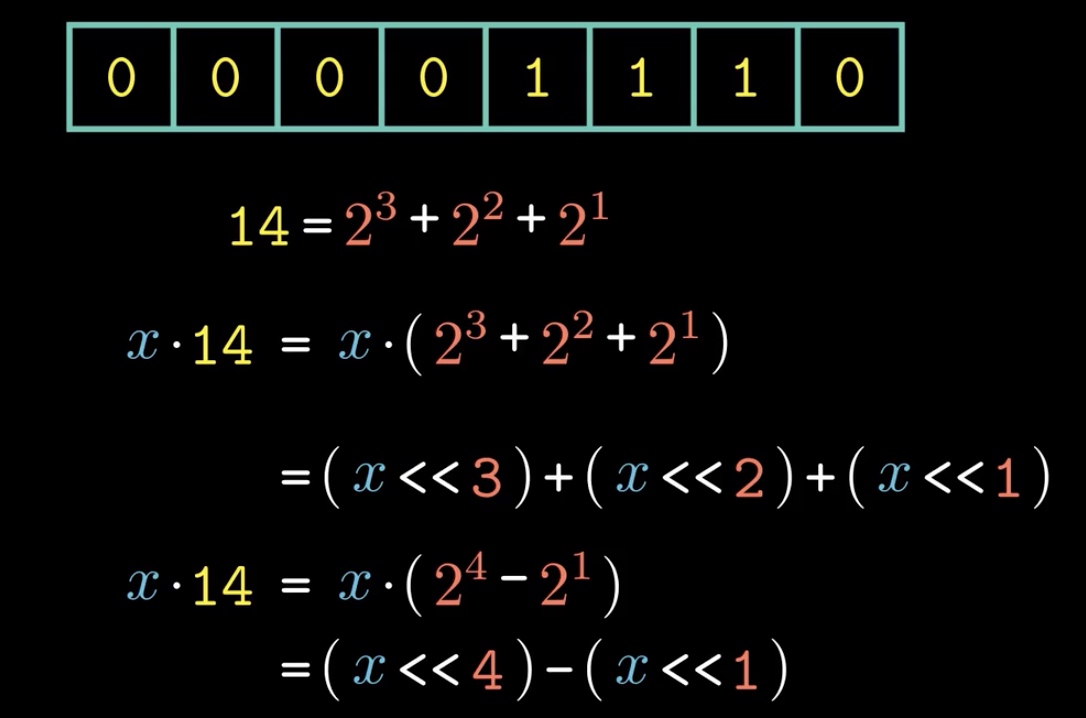
对于有符号乘法（补码乘法）：

计算机的有符号数用补码表示，因此有符号数乘法就是补码乘法。无论是无符号数乘法还是有符号数乘法，运算结果的位级表示都是一样的，只不过补码乘法比无符号数乘法多一步，需要将无符号数转换成补码（有符号数）。虽然完整的乘积结果的位级表示可能会不同，但是截断后的位级表示都是相同的。

除法运算，我们除以2的幂为例进行讨论补码乘除的运算规则：

浮点数

理解浮点数的第一步是考虑含有小数值的二进制数。具体关于二进制权重的理解可以看一下这张图：

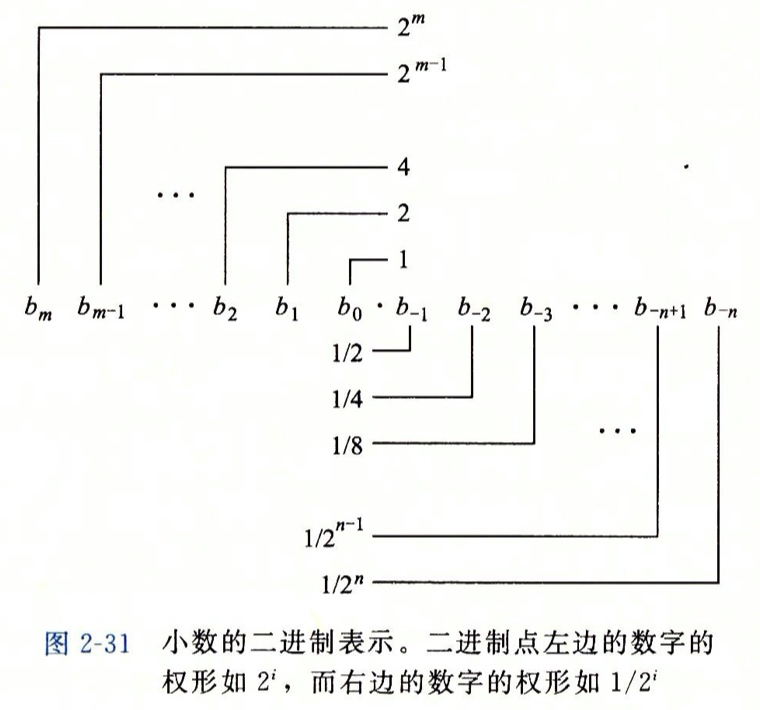
这种定点表示的方法表示出的二进制对应十进制的值关系如下图：

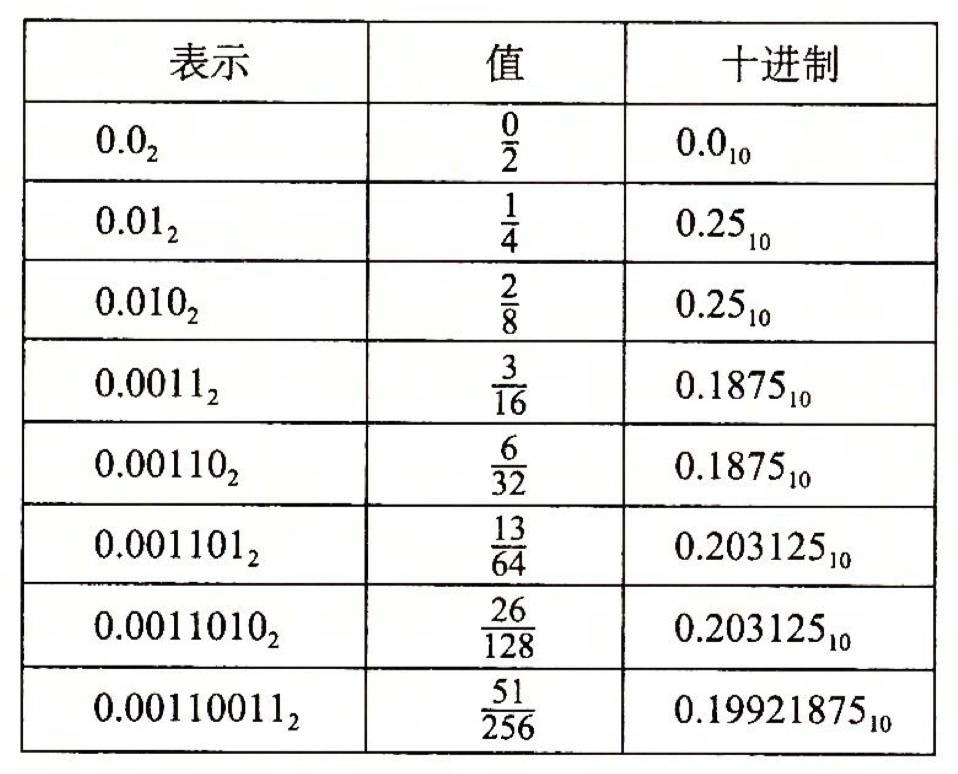
但是我们发现，这样的表示方法非常复杂并且无法表示非常大的数，对于浮点型，我们有另一种IEEE的表示方法，将浮点数分为多个比特位，分别用于表示符号，阶码和尾数等。IEEE关于浮点数的表示公式为：

\[V = (-1)^s \times M \times 2^E \]

其中，s位符号位，s的正负决定了浮点数的正负，E为阶码，尾数为M。以32位float4字节浮点数为例，其占有32个比特位，那么它的符号位、exp、尾数分别划分占用1位、8位和23位，这里需要说明，中间的多个比特位构成的exp并非阶码，想到得到阶码是需要对exp进行相关运算的，后续会说，先看单精度float的表示吧，如下图：

对于double双精度而言，符号位、exp、尾数分别划分占用1位、11位、52位：

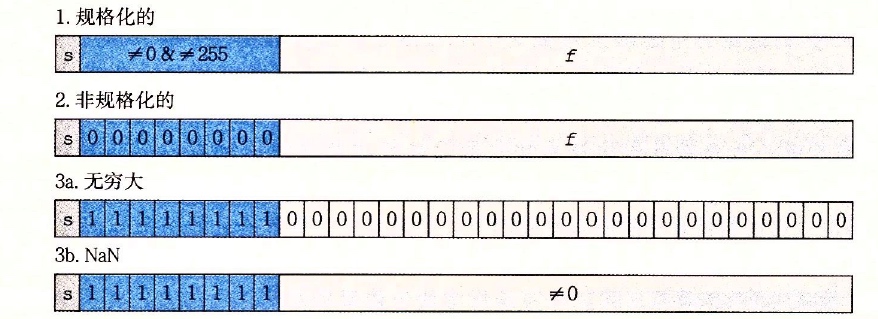
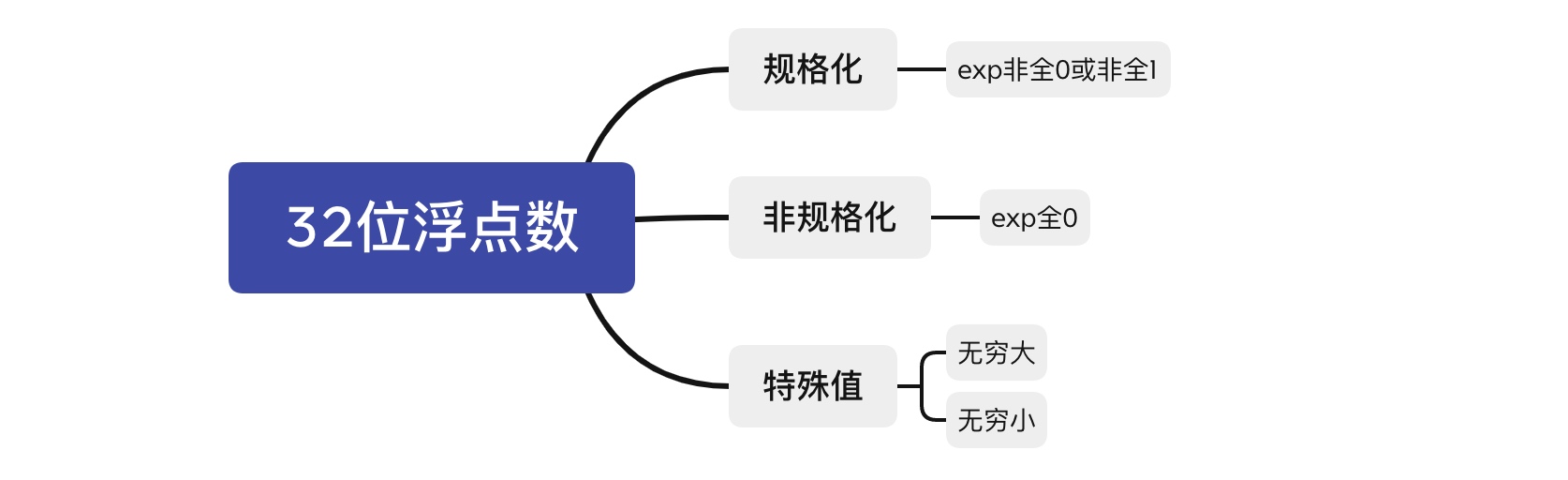
浮点数分为规格化和非规格化的，由阶码决定，拿32尾单精度含8位exp的浮点数来举例，若exp不为0或255，即不全0或不全1，表示的是规格化的数，当exp全0则为非规格化，当exp全1则为特殊值，特殊值分为无穷大和无穷小。

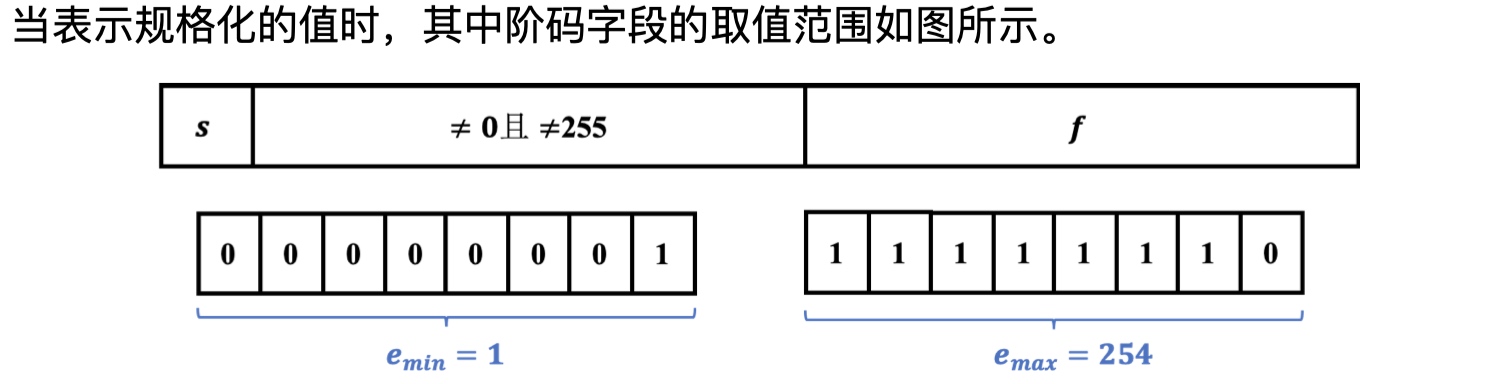
规格化

如上图，对于规格化值，exp的最小值为1，最大值为254，为了方便表述，用e等价于上面图中的exp，来表示8位二进制数，前面我们提到，阶码的运算是需要通过e来得到的，阶码E需要e减去一个偏执量。

\[E = e-\text{bias} \]

非规格化

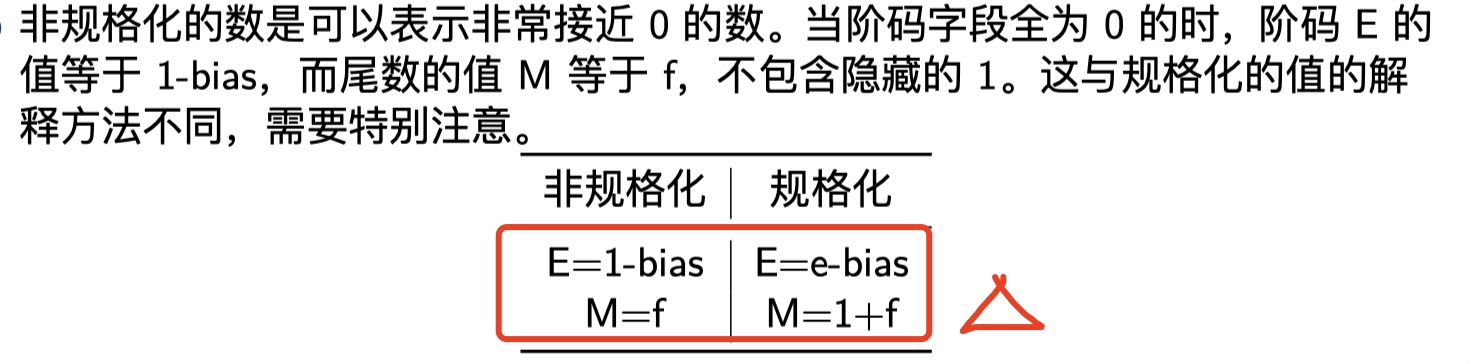
以上说了规格化数的阶码运算以及尾数表示，接下来再来说说非规格化，非规格化的exp为全0，IEEE的表示法中，非规格化表示有两个用途：

1. 提供0值的正负表示。s=0，exp为全0，尾数全0，表示+0；s=1， exp为全0，尾数全0，表示-0。IEEE认为正0和负0在某些方面不同。
2. 非规格化的数可以表示趋于0的数。当exp全0，阶码\(E=1-\text{bias}\)。表示趋于0时的表示方法与规格化表示0的方式不同，区别如下，主要在计算阶码和尾数上：
   

特殊值（无穷大、NaN等）

无穷大的表示分为正负无穷大，对于无穷大，exp全1，尾数部分全为0，正负无穷大的区分在于符号位的正负，s=0表示正无穷大，s=1表示负无穷大。

整型转单精度浮点型

接下来感受一下整型和浮点型之间的转换，以整型转单精度浮点型为例。比如现在将整型12345转换成浮点型12345.0。12345的32位比特位为 :0000 0000 0000 0000 0011 0000 0011 1001，因为高18位均为0，我们只看低14位：11 0000 0011 1001。根据规格化的表示规则，可以将12345表示成如下结果：

\[12345 = 1.1000000111001\times 2^{13} \]

根据IEEE浮点数编码规则M=1+f，所以f的值要对M-1才能得到，小数点左边的1丢弃，由于单精度的小 数字段长度为 23，我们还需要在末端增加10个零：1 0000 0011 1001 0000 0000 00，这样我们就得到浮点数的小数字段了。

接下来因为阶码E=13，由于32位单精度bias=127，所以根据E=e-bias得，e的值为140，二进制表示为：1000 1100，再加上符号位0表示正数，那么最终的结果如下图：

以上则为整型转单精度浮点型的过程实例。