OIer の 寒假训练
\(1-24\)
\(\small{对排序算法的理解}\)
\(\large{\text{Solution}}:\)
挺有意思的一题,原先按照题意模拟考虑轮用一次 \(\text{sort}\) 没想到时限太紧 \(\color{darkblue} T\) 了( \(O(R\cdot n\log n)\) 确实慢),但是根据题解的思想直接把 \(\text{sort}\) 换成 \(\text{stable_sort}\) 居然过了???
题解思路,考虑胜者每轮都 \(+1\) ,负者每轮都不变,因此 胜者所在的集合内部 和 负者所在的集合内部 分数的相对大小关系是不变的,都是有序的。因此问题转化成了将胜负二者这两个有序数列合并的问题,可以采用 \(O(n)\) 的归并排序中的方法来合并,总体复杂度 \(O(R\cdot n)\)。
\(\small{二分加速枚举、线段树、若干水法}\)
\(\large{\text{Solution1}}:\)
可以发现每次区间操作后这段区间的数都会变得更小,因此若一次操作后区间序列不合法(有数字 \(<0\))那么之后的所有操作序列都不再合法;同理,若一次操作后序列仍合法,那么这个操作前的序列也必定合法。这就满足了二分的局部舍弃性(或者是单调性?),可以用一个二分来加速操作的枚举。
具体的,对于每一个 \(\text{mid}\) , 都判断执行了 \(\text{mid}\) 个操作后序列是否合法,以此二分。
\(\large{\text{Solution2}}:\)
先处理出完成 \(m\) 次操作的序列,然后 \(1-n\) 扫一遍,若当前数 \(<0\) 那么将操作从后往前依次撤回,直到整个序列都合法,那么最后一次撤回的操作即为答案。
P3612 [USACO17JAN] Secret Cow Code S
\(\small{递归(分治)}\)
\(\large{\text{Solution}}:\)
可以看出每次操作后的字符串后半部分与上一次的字符串基本一样,所以我们就考虑用这个来递归,每次都会缩小一半的长度。
具体的,若 \(n<\frac{len}{2}\),那么后半部分是没用的,直接 \(len/2\);若 \(n>\frac{len}{2}\) ,那么位置 \(n\) 是由上一个串的位置 \(n-1-len/2\) 翻转得到,递归处理这个子问题即可。
\(1-25\)
\(贪心,带一点博弈论?\)
思考加代码总用时约 1 小时,代码错误:局部变量未初始化,导致UB。
\(\large{\text{Solution}}:\)
不管我们开局选哪个武将 \(x\),和他默契度最高的武将 \(y\) 一定会被电脑抢走。但是默契度次大的武将 \(z\) 我们必然可以取到。因此,全部武将对应默契次大值的最大值即为我们的最优解,同时我们根据机器策略的盲目性,显然可以主动的避免让机器取得优于我们的解,因此人类必胜。
\(贪心\)
刚开始想了10+分钟有了接近正解的思路,但是没有沉住气继续深入思考就直接开始 coding,导致接下来硬钢 90 分钟无果,然后继续深入思考后想出正解,10分钟写完代码。
\(\large{\text{Solution1}}:\)
显然 \(x=n\) 时答案是易得的,而转移到 \(n-1\) 只需删除一个对答案贡献最小的数即可。因此本题使用倒推,维护每个数的贡献,然后每次小根堆删除最小的即可。因为要删数,所以我们还需要一个链表维护前一个数 \(lst_i\) 和后一个数 \(nxt_i\)。
考虑 \(i\) 的贡献:若 \(S_i\) 不是当前未删数字的最大值,那么 \(S_i\) 对答案没有贡献,此时 \(i\) 的贡献
为 \(a_i\);若 \(S_i\) 是最大值,那么删除掉 \(i\) 会使得答案失去 \(S_i-S_{lst_i}\) 这一段,所以此时 \(i\) 的贡献为 \(2\cdot(S_i-S_{lst_i})+a_i\)。由于每一次删数都有可能导致 \(S_i\) 的最大值改变,而且 \(lst_i\) 也在变,因此在删的过程中还有进一步维护每个数的贡献。
\(\large{\text{Solution2}}:\)
距离很烦,所以我们先不考虑距离 ——题解
选 \(x\) 个,最贪心的想,按照 \(a\) 排序选前 \(x\) 大的那几个。其次,我们可以通过将其中的一个(显然也只需要一个)换成另一个 \(S\) 更大的数,也就是用 \(a\) 的贡献换取 \(S\) 的贡献,也可能让答案更优。至于用哪个来换呢,显然使用最小的,也就是第 \(x\) 大的来换。
这题确实挺不错的。
\(1-26\)
\(数学,构造\)
找到了解题的关键但是没有深入思考,导致20分钟后宣告失败,遂看题解。
\(\large{\text{Solution}}:\)
三个变量让我很不喜欢,所以考虑先干掉一个
注意到 \(\dfrac{2}{n}\) 的这个 \(2\) 似乎别有用意,于是尝试把它拆成 \(\dfrac{1}{n}+\dfrac{1}{n}\),原式变为
不妨直接令 \(z=n\),则问题化为求
然后就是小学奥数 \(\dfrac{1}{n+1}+\dfrac{1}{n(n+1)}=\dfrac{1}{n}\) 结束。
闲话:实在太菜了,做黄色的构造题都觉得好难QAQ
\(构造\)
AGC 的题目果然不一般,非常有趣,思路中的细节值得深入思考。思考20分钟无果,遂看题解。
\(\large{\text{Solution}}:\)
考虑什么时候无解:一个数 \(a\) 肯定是在位置 \(a\) 处插入,而往后的插入操作每次都会把一部分数往后推,因此最终序列 \(b\) 有 \(b_i\le i\),否则无解。
最后一次插入是容易的,肯定是一个数 \(i\) 插入到了位置 \(i\) 上。于是我们从后往前找到第一个 \(b_i=i\) 的数,那么他就是最后一次插入操作,把它撤销后序列就变成了上一次操作时的,就变成了子问题,继续找即可。
为什么要从后往前呢?考虑若有 \(b_x=x,b_y=y,x<y\) ,若我们选择撤销 \(x\) 处的插入的话,那么 \(x\) 后面所有的数都要往前挪一个, 也就有 \(b_{y-1}=y>y-1\) ,也就是一开始说的无解的情况。所以要从后往前找。
还是没做出黄题,寄。
\(图论,构造\)
在草稿纸上模拟了10分钟就想出来了,大概是构造一个各部分权值和相同的完全 \(k\) 分图(参加OI-wiki),算是比较友好的题了。
题解的思路非常有参考价值。
\(\large{\text{Solution}}:\)
若无向图(无重边无自环)\(G\) 不连通,则它的补图 \(G'\) 联通。
上述结论的证明 在这里
我们构造一个图,使得此图
- 不连通
- 对于图上的任意顶点,该点和与该点相连的点编号和均为定值 \(S\)
那么这张图的补图就满足
- 连通
- 对于图上的任意顶点,与该点相连的点编号和均为定值
可见满足了题目要求。
具体的,我们将 \(n\) 分奇偶讨论:
若 \(n\) 为奇数,那么我们将连接 \((1,n-1),(2,n-2)\cdots\) ,\(n\) 单独一点。输出补图即可。
若 \(n\) 为偶数,我们连接 \((1,n),(2,n-1)\cdots\),输出补图即可。
看到了个有趣的 \(trick\):不降原则——枚举的时候有序枚举,保证序列不降,可以去重
\(1-27\)
\(记忆化搜索,贪心\)
记搜部分水爆了,但是第二问的前提性质还是挺有思考价值的,证出来以后贪心就做完了。
\(\large{\text{Solution}}:\)
无解的情况搜索的时候直接判掉就好了,下面只考虑有解的情况。
性质:蓄水池能到的干旱地区一定是一个区间
证明的话可以用反证法巴拉巴拉胡一下,大概就是两条不同的路径必有交叉,因此能输水的地方必定连续(没有图不好描述)
记搜的时候就把蓄水池能到的区间左右端点记下来即可,然后第二问就变成了一个区间覆盖整条线段问题,贪心即可。
具体的,将区间按照左端点排序,每次选都选一个左端点在已覆盖范围内且右端点最远的区间来更新。参考
\(搜索剪枝\)
没写,但是其中有一个剪枝非常巧妙。
因该是最优化剪枝的一种,思想就是若当前操作是最优的但还是失败了,那就没必要继续往后尝试了,回溯到以前即可。
具体到本题,就是若选上当前木棍恰好能凑出一根完整木棍(这个操作显然是所有可选操作中最优的),但是往后搜索还是失败了,那就没必要继续尝试用别的木棍凑这根原始木棍了,回溯到上一层。
P3067 [USACO12OPEN] Balanced Cow Subsets G
\(Meet~~in~~middle\),\(bitset\)
非常暴力的思路,思考加coding反反复复一共花了90min,最后用bitset直接贴着最优解的脸。
看了一下题解,思路很巧妙(果然我太蠢了),但是貌似并没有我快(普遍做法 1s,我的做法 200ms)
\(\large{\text{Solution1}}:\)
很暴力的思想,先枚举子集,然后再枚举子集的划分!
数据规模很小但是暴搜又过不了,于是可以考虑折半暴搜搜索。直接把序列分成左右两半,然后分别dfs选子集。
考虑左半部分选出了子集 \(A\),将它分为两部分和分别为 \(a\),\(b\),右半部分选出了子集 \(B\),将它分为两部分和分别为 \(c\),\(d\) ,若两个子集的并为 \(C\) ,要使 \(C\) 合法则应有 \(a+c=b+d\),移项可得 \(a-b=d-c\) 。
这就给我们折半后合并答案提供了思路:我们选定出子集后同样暴力搜索出它的划分方案,称两部分权值的差为 \(A-B\),然后用一个 \(set\) (当然是为了去重)记录下每个集合所有可能划分的 \(A-B\) 的值,合并时利用 \(set\) 保存的信息,判断有多少个左右集合的某个 \(A-B\) 值相同,这些是对答案有贡献的。
具体实现有一点复杂,使用了 bitset 来去重,跑得飞快。
\(\large{\text{Solution2}}:\)
题解巧妙的做法在于:每个数有三种状态,一种是不选,一种是放入1队,最后是放入2队,一个dfs就可以 \(O(3^n)\)。
果然比我的先枚举子集,再枚举子集中的划分这种两层dfs要清新多了,统计答案的时候也是记录 \(A-B\) ,也是将子集二进制压缩来去重(我用的是bitset),感觉大差不差,不知道为什么有些题解比我慢那么多。
\(1-28\)
\(\large{\text{Solution}}:\)
LIS 中用二分维护的 d 数组的意义是维护对于每个DP值得最优转移,比如说求不升子序列的时候,将 \(a_i\) 接在一个恰好 大于他的位置是最优的(小了不行,大太多也浪费),而可以证明这个最优的位置是单调的,因此可以二分维护。
主要就是这什么 \(Dilworth\) 定理:在偏序集中,最小链划分数等于最大反链的长度。
说人话就是,将一个序列划分为多个不相交的不升子序列,最小划分数是这个序列最长上升子序列的长度。
\(1-29~\&~30\)
众所周知,蓝色是水的颜色,这就是一道DP翻译题。(指把题意翻译成DP的转移就过了)
\(\large{\text{Solution}}:\)
每个木头相互独立,而每个格子只能涂一次,因此不难想到把他们设入状态。
设 \(f_{i,j,k,0/1/2}\) 表示涂了 \(j\) 次涂到第 \(i\) 块木板的第 \(k\) 格时,涂 \(0\) 或 \(1\) 或不涂的最大正确数。
然后就有了显而易见的转移,只需要分讨填到第 \(k\) 个的时候的决策即可(翻译题目)。
特别的,有初值
大水,建议降绿
\(贪心,构造\)
半年前月赛里的黄题,不会做,现在还是不会做,果然我一点没有长进。评价是该死的贪心。
\(\large{\text{Solution}}:\)
首先求出每个节点的深度,若深度和 \(sum\) 为奇数显然无解。
问题可以转化为选出某些节点,使其深度和恰好等于 \(\dfrac{sum}{2}\)。考虑到本题一个很重要的性质:因为在树上,因此深度在值域上是连续的。,注意到这一点就可以很容易想到必定是凑出 \(\dfrac{sum}{2}\)。
具体的,我们贪心从大到小扫过去,若可以选就选上,否则找更小的补。
当然如果直接写一个暴搜程序,加上从大到小的排序也是能过的,因为大的数太僵硬不好分配所以先选,小的数灵活可以尽可能满足条件。这个操作可以非常有效的减小搜索树的规模。
\(1-31\)
月末,遇到了一道神仙题,这道题警示我不要在一个困难的思路上死磕,要像广搜一样,接受一些悦动的新灵感,或许会有不一样的收获。
P2501 [HAOI2006] 数字序列 题解
\(DP+找性质\)
sb题调了3个小时,确实神仙细节也确实多:(
\(\large{\text{Solution}}:\)
先看第一问,要求最少改变多少个,其实不太好下手(但是我还是下手了,硬写了快1小时的DP,真蠢啊),考虑补集转化,其实就是求最多保留多少个。手玩一下数据找找性质可以发现,因为要求最后要严格上升,所以若 \(a_i-a_j<i-j\),那么 \(a_i\) 和 \(a_j\) 不能都保留,因为无法改变他两中间的那些数使得这个区间上升(中间数字太多,可用数字太少)。所以设 \(f_i\) 表示保留 \(i\) 则 \(1\) 到 \(i\) 中最多能保留多少个数,易得
但是如果把限制移一下项,就会得到 \(a_i-i\ge a_j-j\),若设 \(b_i=a_i-i\),那么上述转移就是在求 \(b\) 的最长不下降子序列!恭喜你找到本题的性质之一,可以愉快的用 \(O(n\log n)\) 做掉第一问。
获得成就:得到 \(b\) 数组。
现在看第二问,显然修改 \(a_i\) 和修改 \(b_i\) 是等价的,因此就转化为了用最小的修改代价使得 \(b\) 单调不降。
需要修改的显然是不在最长不降子序列中的数。若 \(b_i~,~b_j~(j<i)\) 在最长不降子序列中 且 在子序列中的位置相邻,那么 \(\forall k\in(i,j),b_k<b_j ~or ~ b_k>b_i\)。修改这些 \(k\) 后为了使区间不降,肯定会在值域上形成一段阶梯,考虑如何调整这段阶梯使得代价最小。
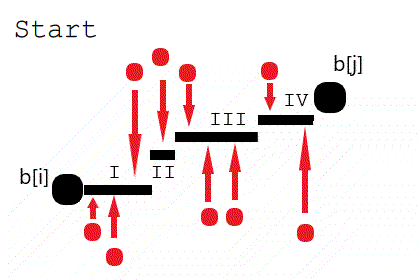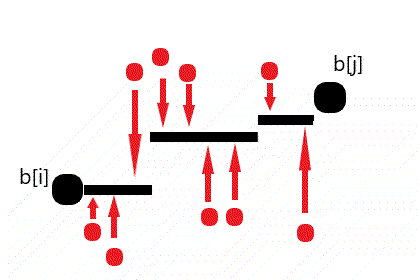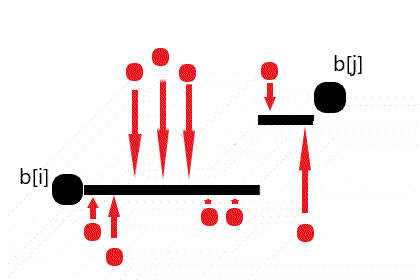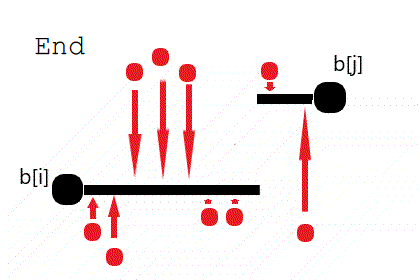
由图可知且可以证明任何最小代价的阶梯样式一定能被转换为上图所示的 ⌊ 存在一个划分点 \(k\in[i,j]\),使得 \(\forall l\in[i,k],b_l=b_i~and~\forall l \in (k,j],b_l=b_j\) ⌉ 的形式。
因此我们只需要枚举分界点 \(k\) 即可找到最小代价。
需要注意,最长不降子序列可能有多个,因此最终求答案的过程还需 DP。设 \(g_i\) 表示保持 \(b_i\) 不变,使得 \([1,i]\) 不降的最小代价。若 \(b_i\) 在最长不降子序列中的前一个数是 \(pre_i\) (显然,\(pre_i\) 可能不是 1 个数),那么有
利用前缀和和数据随机的特性,该算法为 \(O(n^2)\) 。
实现细节就非常有东西了,因为正常情况下最长不降子序列的左右两边都可能有数,因此我们要将 \(b_0\) 和 \(b_{n+1}\) 分别做最小和最大处理,将他们也纳入不降序列当中。其中,\(b_0\) 不能直接设成0,因为 \(b_i\) 的值域可以达到 \(-n\)(两个小时的 experience)。
P2946 [USACO09MAR] Cow Frisbee Team S
\(\large{\text{Solution}}:\)
考虑从限制入手,要让所选数的和为 \(F\) 的倍数,形式化的转换一下就是 \(\bmod F=0\),因此可以想到把 \(\bmod F\) 写入状态,然后就是一个选与不选的DP方程了。
若有代价和价值以及一个限制,那么考虑背包。
背包是一种对(代价,价值)二元关系的合并方式,因此树上DP对子树的合并也即是背包。
\(2-1\)
又打了一场比赛,遇见了一道有趣的题。
\(\large{\text{Solution}}:\)
二进制好题。
在题解里学会了一个好用的玩意
所以题目就转化为了找 \(x~\operatorname{xor}~y=A-2B\),按二进制位考虑,就能发现除最高位有贡献外其他位都是互补没有贡献的,然后这题就做完了。思路即清爽又引人深思,痛快!
然后这场比赛的T3教会我:如果实在调不出来,那就尽早写对拍,否则调死你!
铭记哀痛:2.5h+ 调分块最终 0 分!
若最优解可以通过合并得到,且时间允许,可以考虑区间DP。
区间DP的答案会和区间有关,这里的区间是广义的。
\(2-2\)
树上背包的其实可以理解为dp套dp,因为首先是父节点由子节点合并这一dp操作,其中又蕴含了背包的划分思想——每个子树都有代价和价值,因此合并子树就是 01 分组背包。
但是树上背包的复杂度真的玄学啊,上下界优化正在学习中……
开始学一些不一定用得上的数学。
排序不等式(大小搭配乘不如大配大小配小):
详细证明
接下来介绍一道与之相关的好题(可能 dp 的占比更大一点?)
P2647 最大收益
神题。
考虑选择了 \(s\) 物品,所选的第 \(i\) 个物品的价值为 \(W_i\),代价为 \(R_i\),那么收益为
在选取的物品一样的话,要使收益最大的选取顺序就应该使得 \(\sum\limits_{i=1}^s(s-i)R_i\) 这部分最小,将其拆开
显然只有后半部分跟选取顺序有关,因此考虑将他最大化,那么总体就最小。不难发现这就是排序不等式所支持的形式,当 \(R_i\) 递增时取最大。以上就是我们贪心思路的数学证明,按照 \(R\) 递增的顺序来取可以使得在取得物品相同时受益最大。
接下来就是这题精彩的 DP 了。
按照 \(R\) 递增的顺序,我们尝试设 \(f_i\) 表示考虑了前 \(i\) 个得到的最大收益,但这样是不行的,因为 \(R_i\) 对答案的影响与选了多少个相关。因此我们要将状态升维,设 \(f_{i,j}\) 表示考略了前 \(i\) 个取了 \(j\) 个的最大收益。但还是不行,因为 \(R_i\) 带来的影响与未来的决策选了多少个有关,我们无法在阶段 \(i\) 的时候就知道,也就是说这么设状态是有后效性的,无法转移。
由前往后没有办法了,但可以发现 \(R_i\) 只会对 \(i\) 往后的数的选取造成影响,而对以前没有关系。貌似是一种无前效性?于是我们逆向思维,由后往前:设 \(f_{i,j}\) 表示以 \(i\) 为第一个往后选了 \(j\) 个的最大收益,那么这时 \(R_i\) 的影响就是 \(R_i\cdot(j-1)\) 了。所以我们这样子倒着 DP,就解决了后效性的问题。
至此本题结 这题
说实话,当在题解看到逆向DP的那一刻,有一种颅内高潮的感觉。这不禁令我联想到了在这道题所初见的那个名叫 “费用提前” 的DP优化技巧,令我觉得两者有着莫名的联系。当时就想,这题能不能也用费用提前来做呢?答案是否定的,因为费用提前的前提是 当前决策对未来的影响只与当前决策有关。而反观本题,\(R_i\) 的影响是和后续的决策相关的,因此我认为不能用费用提前来做(当然,这种逆向DP 的方式我觉得就很像费用提前)。
这里埋个伏笔,以后一定要去学!
原来树上背包这种合并蕴含着这么多东西!上下界优化他来了!
还是拿出 这题,普通的树上背包是这么写的:
点击查看代码
void dp(int x)
{
f[x][0]=0;
for(int i=0,v,w;i<g[x].size();i++)
{
v=g[x][i].id;
dp(v);
for(int j=m+(!x);j>=1;j--)
for(int k=1;k<j;k++)
f[x][j]=max(f[x][j],f[v][k]+f[x][j-k]);
}
return ;
}
显然这份代码对于每个节点都要 \(O(nm)\),加上搜索遍历总复杂度为 \(O(n^2m)\)。但是我们其实枚举了很多不必要的状态:
若已经合并了的大小为 \(S\),\(sze_x\) 表示以 \(x\) 为根的子树大小。
- 对于 \(f_{u,j}\),若 \(j>S+sze_u\) 则是无意义的。
- 对于 \(f_{u,j-k}\),若 \(j-k>S\iff k<j-S\) 则是无意义的。
- 对于 \(f_{v,k}\),若 \(k>sze_v\) 则是无意义的。
我们根据上述调整 \(j\),\(k\) 的枚举范围,就被成为上下界优化。最终代码是这样的:
点击查看代码
void dp(int u){
sze[u]=1;
for(auto v:g[u]){
dp(v);
for(int j=min(m+!u,sze[u]+sze[v]);j>=1;j--){
for(int k=max(1,j-sze[u]);k<j&&k<=sze[v];k++){
f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]);
}
}
sze[u]+=sze[v];
}
return ;
}
小编也很难相信,但是事实就是如此,这份代码的复杂度上界骤然变成了 \(O(n^2)\) 的了!
因为每次转移实际上都是两两子树合并的过程,也可以点对点合并的过程。经过上下界优化,所有不必要的状态和转移都被省去了,对于任意点对 \((a,b)\) 只可能在它们的 \(\operatorname{lca}\) 处被合并一次,因此复杂度上界就是 \(O(n^2)\) 的了。
但是我们看代码循环处还对 \(m\) 取了 \(min\),因此复杂度应该跟 \(m\) 也有关系。事实上当 \(m\) 小于 \(n\) 的规模时,可以证明,这个 dp 的复杂度是 \(O(nm)\) 的。
这 是一道针对上下界优化的题,也非常神,卡得非常紧。这里面还有一个 trick,因为直接开二维数组会 MLE,因此直接把二维拍成一维的就可以减少很多原本不必要的空间。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战