最长公共子序列 SSL1463 (动态规划)
题目描述:

解题思路:
这题可以用暴搜枚举每一种可能,找出最优解,然后愉快超时。
分析题目,长度为
n
n
n 的两个序列的最长公共子序列长度必然源于长度
n
−
1
n-1
n−1 的两个序列的最长公共子序列长度,因此可以判断该问题具有最优子结构性,考虑动态规划。
这道题需要用到一种非常经典的线性DP,公共子序列DP。
俗话说得好,几乎每一种模板类型的DP的推出都离不开建模(就是画图!),而分析DP的办法最好就是打表,因此,在我们完全不知道DP方程的情况下,我们可以出一个小一点的数据,尝试打个表,自己推出DP
设这题数据为:
序列X为
2
4
6
7
\ \ \ \ 2\ \ \ \ 4\ \ \ \ 6\ \ \ \ 7
2 4 6 7
序列Y为
2
3
4
7
\ \ \ \ 2\ \ \ \ 3\ \ \ \ 4\ \ \ \ 7
2 3 4 7
把不同长度情况下序列的最长公共子序列的长度列出来:
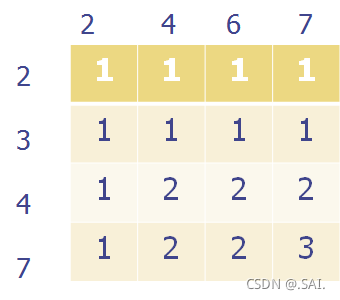
先不说啥,设定状态,我们用
d
p
i
,
j
dp_{i,j}
dpi,j 表示表格中第
i
i
i 行第
j
j
j 列的数,其中,
d
p
i
,
j
dp_{i,j}
dpi,j 表示从 X 序列的第
i
i
i 个到 Y 序列的第
j
j
j 个之间的最长公共子序列的长度。
我们用DP的思维方式来模拟填表过程。
首先看到
X
1
X_1
X1 和
Y
1
Y_1
Y1,相等。很明显,由于
X
1
X_1
X1 和
Y
1
Y_1
Y1 的相等,
d
p
1
,
1
dp_{1,1}
dp1,1 很明显就等于1,意味着在
X
1
−
1
X_{1-1}
X1−1 和
Y
1
−
1
Y_{1-1}
Y1−1 这个区间内,由于元素的相等,使得公共子序列长度增加了1。
但是这样这太肤浅了,我们需要明白的是——这里是怎么变成 1 的。
还记得,我们上文说该问题具有最优子结构性。没错,这就是问题解决的关键。众所周知,任何具有最优子结构性问题的最优解,都是在子问题的最优解之上得来的。,明白了这个定义,我们就能明白图中的 d p 1 , 1 dp_{1,1} dp1,1 是怎么得出来的。
最长公共子序列具有最优子结构性质,设序列 X = X 1 , X 2 , … … X m X={ X_1,X_2, ……X_m } X=X1,X2,……Xm, Y = Y 1 , Y 2 … … , Y n Y={Y_1,Y_2……,Y_n} Y=Y1,Y2……,Yn 的最长公共子序列为 Z = Z 1 , Z 2 … … Z k Z={Z_1,Z_2……Z_k} Z=Z1,Z2……Zk
若
X
m
=
Y
n
X_m=Y_n
Xm=Yn,则
Z
k
=
X
m
=
Y
n
Z_k=X_m=Y_n
Zk=Xm=Yn,且
Z
k
−
1
Z_k-1
Zk−1 是
X
m
−
1
X_m-1
Xm−1 和
Y
n
−
1
Y_n-1
Yn−1 的最长公共子序列,因此
d
p
m
,
n
=
d
p
m
−
1
,
n
−
1
+
1
dp_{m,n}=dp_{m-1,n-1}+1
dpm,n=dpm−1,n−1+1
若
X
m
!
=
Y
n
X_m\ !=Y_n
Xm !=Yn,则
d
p
m
,
n
=
m
a
x
(
d
p
m
−
1
,
n
,
d
p
m
,
n
−
1
)
dp_{m,n}=max(dp_{m-1,n}\ ,\ dp_{m,n-1})
dpm,n=max(dpm−1,n , dpm,n−1)。
再简单一点,按表格的形式来说,就是如果
X
m
=
Y
n
X_m=Y_n
Xm=Yn,那么
d
p
m
,
n
dp_{m,n}
dpm,n 等于表格中左上角的数 +1,否则等于表格左边和表格上面中稍大的数。
固有状态转移方程:
若 X m = Y n X_m=Y_n Xm=Yn, d p m , n = d p m − 1 , n − 1 + 1 dp_{m,n}=dp_{m-1,n-1}+1 dpm,n=dpm−1,n−1+1
否则 d p m , n = m a x ( d p m − 1 , n , d p m , n − 1 ) dp_{m,n}=max(dp_{m-1,n}\ ,\ dp_{m,n-1}) dpm,n=max(dpm−1,n , dpm,n−1)
CODE:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
string str1,str2;
char a[1001],b[1001];
int dp[1001][1001]={0},ans=0;
void input()
{
cin>>str1>>str2;
for(int i=0;i<str1.size();i++)
a[i+1]=str1[i];
for(int i=0;i<str2.size();i++)
b[i+1]=str2[i];
}
void DP()
{
for(int i=1;i<=str1.size();i++)
{
for(int j=1;j<=str2.size();j++)
{
if(a[i]==b[j])
dp[i][j]=dp[i-1][j-1]+1;
else
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
ans=max(ans,dp[i][j]);
}
}
cout<<ans;
}
int main()
{
input();
DP();
return 0;
}
总结:
DP的方程分析应该从子问题考虑。
能在鄙人这里得到一丁点启发的朋友们,欢迎留下你们的支持!!:)
如果你喜欢我的内容,那么也请支持一下他吧





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战