[NOIP2018模拟赛10.22]咕咕报告
闲扯
这是篇咕咕了的博客
考场上码完暴力后不知道干什么,然后忽然发现这个T1好像有点像一道雅礼集训时讲过的CF题目 Rest In Shades ,当时那道题还想了挺久不过思路比较妙,于是我就也\(yy\)出了一个二分+前缀和的做法
首先这道题求点双之后每个点就是原来一个环,我们在求点双时记录出每个点双的最小mi和最大标号mx,那么越过[mi,mx]这段区间就是违法的(区间[a,b]越过,即覆盖是指\(a<=mi,b>=mx\)),于是我们对于可以对于每段这种区间记录之前有多少个合法的
最后二分+前缀和搞一搞就好了,但是发现计算之前有多少多少个合法的似乎很难搞...
T1 graph
我们还是点双缩点求出违法区间,同时对于每个坐标求出个\(rb[i]\),表示以\(i\)为左端点,合法区间右端点最远到哪里,怎么求这个?
不知道可不可以log地去做,想了想好像没想到什么好办法.但是这个\(rb[i]\)有个性质就是满足单调的,左边数字的\(rb\)显然不可能大于右边数字的\(rb\)
于是我们可以线性地扫一遍得到\(rb[i]\),对于一个非法区间\([l,r]\)如果左端点在\(l\)的左边(包括l)我们是不可能覆盖到\(r\),我们为了处理方便将其转化成\([l,r-1]\)这样的区间.发现rb值可能会是下图中的情况
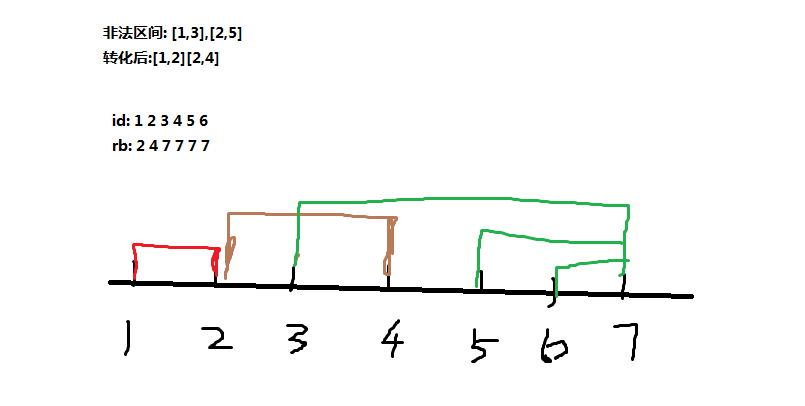
一开始我们需要将所有\(rb[i]\)置为\(n\),然后从右往左扫(因为我们的rb值是要取min的,从左往右扫是错误的,可以手动模拟下)得到所有rb值
这样的话对于一个询问\([l,r]\)。根据单调性,我们可以二分找到一个最小的点\(x\)使得\(rb[x]>=r\),同时用前缀和记录\(l\)到\(i\)的答案
注意这里的前缀和是指\(i\)到\(rb[i]\)这个合法区间内,\(i\)能产生的合法数对贡献之和,我们可以在求\(rb[i]\)的过程中求出
所以由于\([l,x-1]\)中的\(rb[i]\)都小于\(r\)所以是可以直接前缀和计算的,而\(x\)到\(r\)这部分都是合法区间直接暴力算就好了
话说这道题求环要么DFS要么用点双,一开始SB地用了边双...因为边双中可能会包含多个环,这样的话小区间就算不到了
然而不知道怎么回事卡死在80分...不知道哪错了
/*
code by RyeCatcher
*/
const int maxn=600005;
const int inf=0x7fffffff;
int rb[maxn],fa[maxn],dep[maxn];
bool vis[maxn];
int a[maxn];
ll ans[maxn];
struct Edge{
int ne,to;
}edge[maxn<<1];
int h[maxn],num_edge=1;
int n,m,q;
inline void add_edge(int f,int to){
edge[++num_edge].ne=h[f];
edge[num_edge].to=to;
h[f]=num_edge;
}
int dfn[maxn],low[maxn],st[maxn],tot=0,top=0;
void tarjan(int now,int fa){
int v;
st[++top]=now;
dfn[now]=low[now]=++tot;
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa)continue;
if(!dfn[v]){
tarjan(v,now);
low[now]=min(low[now],low[v]);
if(low[v]>=dfn[now]){
int x=st[top],c=0,mi=inf,mx=-inf;
do{
c++;
x=st[top];
//printf("--%d ",x);
mi=min(mi,x);
mx=max(mx,x);
top--;
}while(x!=v);
//printf("%d **%d\n",now,c+1);
c++,mi=min(mi,now),mx=max(mx,now);
if(c>2)rb[mi]=mx-1;
}
}
else low[now]=min(low[now],dfn[v]);
}
return ;
}
int main(){
int x,y;
freopen("graph7.in","r",stdin);
freopen("graph7.ans","w",stdout);
//FO(graph);
read(n),read(m);
for(ri i=1;i<=m;i++){
read(x),read(y);
add_edge(x,y);
add_edge(y,x);
rb[i]=n;
}
for(ri i=m+1;i<=n;i++)rb[i]=n;
dep[1]=1,fa[1]=0;
for(ri i=1;i<=n;i++)if(!dfn[i])tarjan(i,0);
//for(ri i=1;i<=n;i++)printf("--%d %d--\n",i,rb[i]);
ans[n]=1,rb[n]=n;
for(ri i=n-1;i>=1;i--){
rb[i]=min(rb[i+1],rb[i]);
ans[i]=ans[i+1]+(rb[i]-i+1);
}
read(q);
int l,r,t,mid,L,R;
//for(ri i=1;i<=n;i++)printf("%d %d %d\n",i,rb[i],ans[i]);
while(q--){
read(L),read(R);
l=L,r=R;
while(l<=r){
mid=(l+r)>>1;
if(rb[mid]<R)l=mid+1;
else t=mid,r=mid-1;
}
//printf("%d %d %d--\n",L,R,t);
//printf("%d\n",t);
printf("%llu\n",(ans[L]-ans[t]+1ll*(R-t+2)*1ll*(R-t+1)/2));
}
return 0;
}
T2 kite
-
前置技能点
-
nlogn 二分求LIS
-
动态维护RMQ
-
毒瘤题,考场上直接弃疗了
终于看大佬的博客看懂了:https://blog.csdn.net/zearot/article/details/50857353
简单来说将\(h[id]\)修改为\(dta\)后序列的LIS的长度分两种情况考虑:
Case#1
修改后a[id]所在的LIS的长度
Case#2
修改后a[id]不在的LIS中
Case#2.1
原序列的\(LIS\)中必须经过原来的\(a[id]\),那么此时为原来LIS长度-1
Case#2.2
原序列的\(LIS\)可以不经过原来的\(a[id]\),那么此时为原LIS长度
我们将的答案就是\(max(ans_{case1},ans_{case2})\)
处理Case#1
考虑怎么离线求修改后的\(a[id]\)所在LIS长度,个人感觉还是比较妙的
我们在nlogn二分求LIS的时候正过来求一遍LIS,反过来求一遍最长下降子序列就可以得到\(fr[i],fl[i]\)分别表示以\(i\)结尾/开头的LIS长度
发现\(a[id]\)修改为dta过后的\(LIS\)长度即为\(max(fr[i])_{i<id , h[i]<dta}+max(fl[j])_{i>id , h[i]>dta}\)
这是个有两个约束条件(下标和h值)的max,处理方法第一次接触:
对于处理左边的\(max\),我们从左往右加数,使得下标满足条件,同时线段树中我们将\(h[i]\)值作为下标(所以需要离散化),储存fr[i]
这样的话你在区间\([1,h[id]-1]\)查询最大值就可以了,大佬都是用树状数组,我只会SB线段树
右边情况类似
处理Case#2
主要一条性质:如果LIS中某数排名为\(x\),那么在所有LIS中它的排名都是\(x\)
有了这个性质就比较好判断原来LIS是否必须需要某数
代码
/*
code by RyeCatcher
*/
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cctype>
#include <utility>
#include <queue>
#include <vector>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <iostream>
#define DEBUG freopen("dat.in","r",stdin);freopen("wa.out","w",stdout);
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define ri register int
#define ll long long
#define ull unsigned long long
#define SIZE 1<<22
using std::min;
using std::max;
using std::lower_bound;
using std::queue;
using std::vector;
using std::pair;
using namespace __gnu_pbds;
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=gc())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=gc())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int maxn=600005;
const int inf=0x7fffffff;
int fl[maxn],fr[maxn],len=0,a[maxn];
int n,m,h[maxn],k;
inline void dp(){
int x;
len=0,a[0]=-inf;
for(ri i=1;i<=n;i++){
if(h[i]>a[len])fr[i]=++len,a[len]=h[i];
else{
x=lower_bound(a+1,a+1+len,h[i])-a;
a[x]=h[i];
fr[i]=x;
}
}
k=len;
len=0,a[0]=-inf;
for(ri i=n;i>=1;i--){
if(h[i]<-a[len])fl[i]=++len,a[len]=-h[i];
else{
x=lower_bound(a+1,a+1+len,-h[i])-a;
a[x]=-h[i];
fl[i]=x;
}
}
return ;
}
#define pii pair<int,int>
#define fst first
#define scd second
cc_hash_table <int,int> g;
int fafa[maxn<<5];
int cnt=0;
inline void discreate(){
int x,y,tot=0;
std::sort(fafa+1,fafa+1+cnt);
cnt=std::unique(fafa+1,fafa+1+cnt)-(fafa+1);
//printf("%d\n",cnt);
for(ri i=1;i<=cnt;i++){
x=fafa[i];
if(!g[x]){
g[x]=++tot;
//f[tot]=g[x];
}
}
return ;
}
pii qry[maxn];
vector <int> qwq[maxn];
int pos[maxn],pcnt[maxn];
int L,R,dta,t,ans=0;
struct Segment_Tree{
int mx[maxn<<3];
void update(int now,int l,int r){
if(l==r){
mx[now]=dta;
return ;
}
int mid=(l+r)>>1;
if(t<=mid)update(now<<1,l,mid);
else update(now<<1|1,mid+1,r);
mx[now]=max(mx[now<<1],mx[now<<1|1]);
return ;
}
void query(int now,int l,int r){
if(L<=l&&r<=R){
ans=max(ans,mx[now]);
return ;
}
int mid=(l+r)>>1;
if(L<=mid)query(now<<1,l,mid);
if(mid<R)query(now<<1|1,mid+1,r);
return ;
}
}T1,T2;
int lol[maxn],ror[maxn];
inline void solve(){
int id,x,y;
for(ri i=1;i<=n;i++){
for(ri j=0;j<qwq[i].size();j++){
id=qwq[i][j];
L=1,R=g[qry[id].scd]-1;
ans=0;
if(L<=R)T1.query(1,1,cnt);
lol[id]=ans;
}
t=g[h[i]],dta=fr[i];
T1.update(1,1,cnt);
}
for(ri i=n;i>=1;i--){
for(ri j=0;j<qwq[i].size();j++){
id=qwq[i][j];
L=g[qry[id].scd]+1,R=cnt;
ans=0;
if(L<=R)T2.query(1,1,cnt);
ror[id]=ans;
//printf("%d %d %d %d %d %d\n",i,ror[id],qry[id].scd,cnt,L,R);
}
t=g[h[i]],dta=fl[i];
T2.update(1,1,cnt);
}
return ;
}
int main(){
int x,y;
//FO(kite);
freopen("kite5.in","r",stdin);
freopen("kite5.ans","w",stdout);
read(n),read(m);
for(ri i=1;i<=n;i++){
read(h[i]);
fafa[++cnt]=h[i];
}
dp();
for(ri i=1;i<=n;i++){
if(fl[i]+fr[i]==k+1){
if(!pcnt[fr[i]])pos[i]=fr[i],pcnt[fr[i]]++;
else pcnt[fr[i]]++;
}
}
//for(ri i=1;i<=n;i++)printf("%d %d %d %d %d\n",k,i,h[i],fl[i],fr[i]);
for(ri i=1;i<=m;i++){
read(qry[i].fst),read(qry[i].scd);
qwq[qry[i].fst].push_back(i);
fafa[++cnt]=qry[i].scd;
}
discreate();
solve();
for(ri i=1;i<=m;i++){
y=qry[i].fst;
if(h[y]==qry[i].scd){
printf("%d\n",k);
continue;
}
if(pos[y]){
if(pcnt[pos[y]]==1)x=k-1;
else x=k;
}
else x=k;
//printf("--%d %d--\n",lol[i],ror[i]);
printf("%d\n",max(lol[i]+ror[i]+1,x));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号