[JZOJ100019]A--dfn序+扫描线
[JZOJ100019]A--dfn序+扫描线
题目链接
太懒了自行搜索
分析
这道题查了一个下午的错,真的心态崩了
不过这道题确实妙啊
类比于喝喝喝,我们发现任何一条覆盖了非法路径的路径一定不合法,假如非法路径为\((x,kx)\),设\(u\)为\(dfn\)序中较小的那个点,\(v\)为较大的那个;假如覆盖了路径\((u,v)\)的路径为\((a,b)(dfn_a<dfn_b)\);
设数组\(ed[x]\)为\(x\)的子树中\(dfs\)最大的那个点的\(dfs\)序,显然这可以和\(dfs\)序在一遍\(dfs\)中求出
我们还需要知道:\(x\) 的子树中\(dfs\)序是连续的一段
考虑两种情况:
-
\(u\)是\(lca(u,v)\),分析发现这也有两种情况
先设\(g\)为路径\((u,v)\)上距\(u\)最近的那个点-
Case#1
\(dfn[v]<=dfn[a]<=ed[v]\) , \(dfn[b]>ed[g]\)
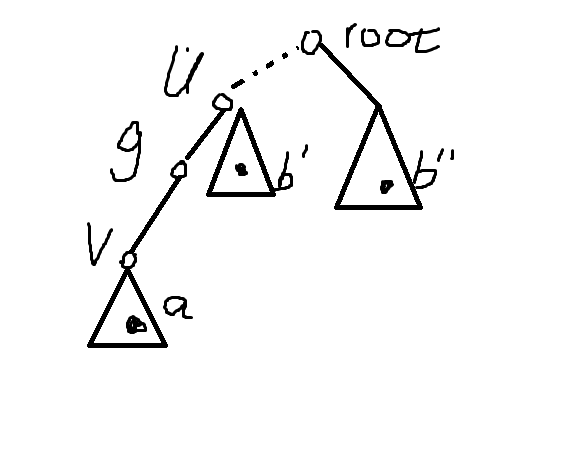
-
Case#2
\(dfn[v]<=dfn[b]<=ed[v]\) , \(dfn[g]>dfn[a]\)
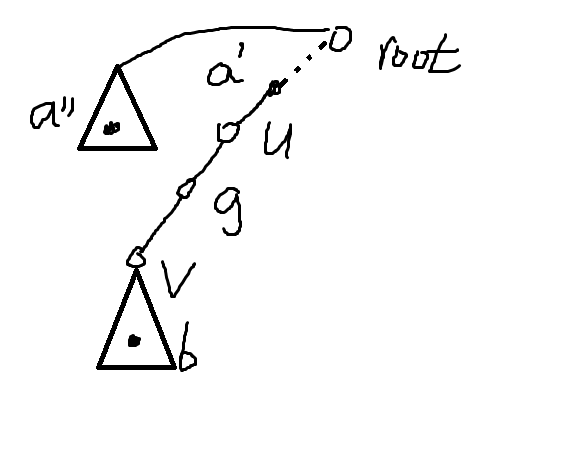
-
-
\(u\)不是\(lca(u,v)\)
这个只有一种情况,\(a,b\)分别在\(u,v\)子树中,即
Case#3
\(dfn[u]<=dfn[a]<=ed[u]<=dfn[v]<=dfn[b]<=ed[v]\)
我们把\((a,b)\)看成一个有序数对的话,发现其实每一种\(case\)都围成了一个矩形,我们只需要求出矩形面积的并之后即可得出所有不合法的路径,用总路径数\(n*(n-1)/2\)减去不合法即所求
求矩形面积的并使用线段树的扫描线法,但是发现一个点我们也要算进贡献,并非严格意义的二维图形;
因为值域很小\((1e5)\),学会了一种船新操作,我们不排序,将纵坐标相同的丢入一个容器,直接从小到大钦定纵坐标.不断取出对应容器内的线段加入,然后计算剩余的点数即可(纵坐标已钦定)
一道图论题转化成了数据结构,也是精妙啊
代码
/*
code by RyeCatcher
*/
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=gc())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=gc())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int maxn=500005;
const int inf=0x7fffffff;
int n;
struct Edge{
int ne,to;
}edge[maxn<<1];
int h[maxn],num_edge=1;
int fa[maxn][17];
inline void add_edge(int f,int to){
edge[++num_edge].ne=h[f];
edge[num_edge].to=to;
h[f]=num_edge;
}
int dfn[maxn],ed[maxn],dep[maxn],tot=0;
void dfs(int now){
int v;dfn[now]=++tot;
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa[now][0]||dfn[v])continue;
dep[v]=dep[now]+1,fa[v][0]=now;
for(ri i=1;i<=16;i++)fa[v][i]=fa[fa[v][i-1]][i-1];
dfs(v);
}
ed[now]=tot;
return ;
}
int get_g(int x,int y){//x到y路径上距y最近
for(ri i=16;i>=0;i--){
//printf("%d %d\n",fa[x][i],x);
if(dep[fa[x][i]]>dep[y]){
x=fa[x][i];
//printf("%d\n",x);
}
}
return x;
}
int L,R,dta;
struct Seg{
int l,r,h,d;
Seg(){l=r=h=d=0;}
Seg(int _l,int _r,int _h,int _d){l=_l,r=_r,h=_h,d=_d;}
}seg[maxn<<4];
int poi=0;
ll sum[maxn<<2];
ll tag[maxn<<2];
vector <int> dd[maxn];
inline void modify(int now,int l,int r){
if(tag[now]>0)sum[now]=(r-l+1);
else sum[now]=sum[now<<1]+sum[now<<1|1];
}
void update(int now,int l,int r){
if(L<=l&&r<=R){
tag[now]+=dta;
modify(now,l,r);
return ;
}
int mid=(l+r)>>1;
if(L<=mid)update(now<<1,l,mid);
if(mid<R)update(now<<1|1,mid+1,r);
modify(now,l,r);
return ;
}
ll ans=0;
int main(){
int x,y,ex,ey,g;
FO(a);
//freopen("a5.in","r",stdin);
read(n);
for(ri i=1;i<n;i++){
read(x),read(y);
add_edge(x,y);
add_edge(y,x);
}
dep[1]=1,fa[1][0]=0;
dfs(1);
int p,q;
for(ri i=1;i<=n;i++){
for(ri j=i+i;j<=n;j+=i){
p=i,q=j;
if(dfn[p]<dfn[q])swap(p,q);
x=dfn[p],y=dfn[q];
ex=ed[p],ey=ed[q];
if(x>=y&&x<=ey){
g=get_g(p,q);
dd[x].push_back(++poi);
seg[poi]=Seg(1,dfn[g]-1,x,1);
dd[ex+1].push_back(++poi);
seg[poi]=Seg(1,dfn[g]-1,ex,-1);
if(ed[g]==n)continue;
dd[ed[g]+1].push_back(++poi);
seg[poi]=Seg(x,ex,ed[g]+1,1);
dd[n+1].push_back(++poi);
seg[poi]=Seg(x,ex,n,-1);
}
else {
dd[x].push_back(++poi);
seg[poi]=Seg(y,ey,x,1);
dd[ex+1].push_back(++poi);
seg[poi]=Seg(y,ey,ex,-1);
}
}
}
for(ri i=1;i<=n;i++){
for(ri j=0;j<dd[i].size();j++){
x=dd[i][j];
L=seg[x].l,R=seg[x].r,dta=seg[x].d;
update(1,1,n);
}
ans+=sum[1];
}
printf("%lld\n",1ll*n*(n-1)/2-ans);
return 0;
}


