学习笔记--线段树合并与分裂
前言
集训时侯讲了一道线段树神题,看题解时FA现需要一个叫"线段树合并"的前置技能点,于是就补了这个坑顺便了解一下线段树的分裂
需要前置技能点:
-
线段树
- 动态开点权值线段树
参考链接
https://wenku.baidu.com/view/88f4e134e518964bcf847c95.html
https://www.cnblogs.com/Mychael/p/8665589.html
https://www.cnblogs.com/zzqsblog/p/6181434.html
分析
这里的线段树合并是针对动态开点的权值线段树而言的,线段树合并与分裂可以快速合并一些信息或分裂区间,完成一些查询区间第\(k\)大等奇奇怪怪的操作
合并Merge
代码
int merge(int x,int y){
/*合并x和y*/
if(!x)return y;
if(!y)return x;
int t=new_node();
sum[t]=sum[x]+sum[y];
ls[t]=merge(ls[x],ls[y]);
rs[t]=merge(rs[x],rs[y]);
return t;
}
时间复杂度博客中都说是\(O(N \log N)\),不过证明都感觉不太理解
分裂Split
代码
void split(int &now,int &po,int l,int r,int k){
/*将now中前k个分裂到po中去*/
if(!now)return ;
if(!po)po=new_node();
if(l==r){
sum[now]-=k,sum[po]+=k;
return ;
}
int tt=sum[ls[now]],mid=(l+r)>>1;
if(k<tt)split(ls[now],ls[po],l,mid,k);
else ls[po]=ls[now],ls[now]=0;
if(tt<k){
split(rs[now],rs[po],mid+1,r,k-tt);
}
pushup(now),pushup(po);
return ;
}
时间复杂度看上去也像\(O(N \log N)\)
数组大小
这个不怎么会算,因为这个RE/MLE了好多发,考场上建议拿极限数据跑一跑看看会不会RE
例题
luogu3605竞升者计数
https://www.luogu.org/problemnew/show/P3605
分析
不错的上手题,像可并堆一样自底向上合并同时不断统计答案
代码
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cctype>
#include <iostream>
#include <queue>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#define ll long long
#define ri register int
using std::min;
using std::max;
using namespace __gnu_pbds;
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while(!isdigit(c=getchar()))ne=c=='-';
x=c-48;
while(isdigit(c=getchar()))x=(x<<3)+(x<<1)+c-48;
x=ne?-x:x;return ;
}
const int maxn=200005;
const int inf=0x7fffffff;
struct Edge{
int ne,to;
}edge[maxn];
int h[maxn],num_edge=1;
inline void add_edge(int f,int to){
edge[++num_edge].ne=h[f];
edge[num_edge].to=to;
h[f]=num_edge;
}
gp_hash_table <ll,int> g;
int rt[maxn],sum[maxn<<2],f[maxn],tot=0;
int ls[maxn],rs[maxn];
int n,v[maxn],cnt=0;
int L,R,t;
int ans=0,anss[maxn];
void query(int now,int l,int r){
if(L<=l&&r<=R){
ans+=sum[now];return ;
}
int mid=(l+r)>>1;
if(L<=mid)query(ls[now],l,mid);
if(mid<R) query(rs[now],mid+1,r);
return ;
}
void update(int &now,int l,int r){
if(!now)now=++cnt;
sum[now]++;
if(l==r)return ;
int mid=(l+r)>>1;
if(t<=mid)update(ls[now],l,mid);
else update(rs[now],mid+1,r);
return ;
}
int merge(int x,int y){
if(!x)return y;
if(!y)return x;
int t=++cnt;
sum[t]=sum[x]+sum[y];
ls[t]=merge(ls[x],ls[y]);
rs[t]=merge(rs[x],rs[y]);
return t;
}
void dfs(int now){
for(ri i=h[now];i;i=edge[i].ne){
dfs(edge[i].to);
merge(rt[now],rt[edge[i].to]);
}
L=v[now]+1,R=tot;
ans=0;
query(1,1,n);
anss[now]=ans;
t=v[now];
update(rt[now],1,tot);
}
int main(){
int x,y;ll z;
read(n);
for(ri i=1;i<=n;i++){
read(z);
if(!g[z]){
g[z]=++tot;
f[tot]=z;
}
v[i]=g[z];
}
for(ri i=2;i<=n;i++){
read(i);
add_edge(i,x);
}
dfs(1);
for(ri i=1;i<=n;i++)printf("%d\n",anss[i]);
return 0;
}
luogu3521 Tree Rotations
https://www.luogu.org/problemnew/show/P3521
分析
一个显然的性质,DFS序中子树是一段连续区间,对于节点\(x\)的儿子节点\(son[x][i]\),交换它们之间的顺序对除\(x\)子树外的逆序对顺序不会造成任何影响,所以我们只考虑贪心地交换儿子节点使产生的逆序对最少就好了
但是考虑怎么在分别计算交换与不交换两棵线段树\(Tx,Ty\)各自产生的贡献,我们分治地考虑这个问题,假设一开始\(Tx\)在左边,那么不交换的话答案就是\(Tx,Ty\)中各自逆序对个数加上\(\sum_i^{size[Tx]} \sum_j^{size[Ty]}[a[i]>a[j]]\)
前面的答案我们可以在自下而上合并中统计出来,但是考虑右边那个怎么算
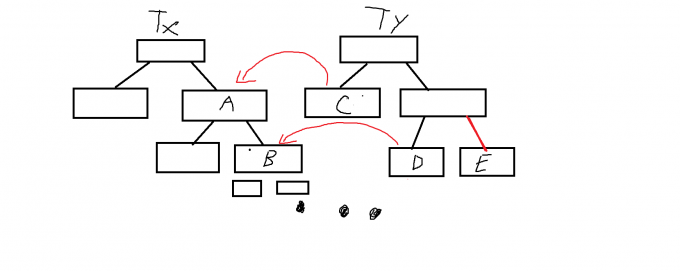
这里还是不交换的情况,首先C区间肯定是会对A区间产生贡献(显然,这里的区间是值域区间),但是可能会忽略掉一些\(Tx\)在A区间中的数比\(Ty\)对应区间还要小的情况,所以我们还要加上\(D\)对\(B\)的贡献,以此类推,当然左区间也要递归
考虑交换的情况类似,反过来就好,不多说
然后这些可以在合并时计算出来
代码
// luogu-judger-enable-o2
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <queue>
#include <vector>
#define SIZE 1926081
#define ll long long
#define ri register int
using std::min;
using std::max;
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
#ifdef RyeCatcher
#define gc getchar
#endif
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while(!isdigit(c=gc()))ne=c=='-';x=c-48;
while(isdigit(c=gc()))x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int N=100005;
const int maxn=2000005;
const int inf=0x7fffffff;
int sum[maxn<<2],ls[maxn<<2],rs[maxn<<2];
int son[N<<2][2],ss=0;
int n,rot,rt[N<<2],tot=0;
ll val[N<<2];
ll cnt1,cnt2,ans=0;
int init(){
int x;
read(x);
ss++;
if(!x){
x=ss;
son[x][0]=init();
son[x][1]=init();
}
else{
val[ss]=x;
x=ss;
}
return x;
}
int merge(int x,int y){
if(!x)return y;
if(!y)return x;
int t=++tot;
sum[t]=sum[x]+sum[y];
cnt1+=1ll*sum[ls[x]]*sum[rs[y]];
cnt2+=1ll*sum[rs[x]]*sum[ls[y]];
ls[t]=merge(ls[x],ls[y]);
rs[t]=merge(rs[x],rs[y]);
return t;
}
int t;
void update(int &now,int l,int r){
if(!now)now=++tot;
sum[now]++;
if(l==r)return ;
int mid=(l+r)>>1;
if(t<=mid)update(ls[now],l,mid);
else update(rs[now],mid+1,r);
return ;
}
void dfs(int now){
if(val[now]){
t=val[now];
update(rt[now],1,n);
return ;
}
dfs(son[now][0]);
dfs(son[now][1]);
cnt1=cnt2=0;
rt[now]=merge(rt[son[now][0]],rt[son[now][1]]);
ans+=min(cnt1,cnt2);
return ;
}
int main(){
read(n);
rot=init();
dfs(rot);
printf("%lld\n",ans);
return 0;
}
luogu2824排序
https://www.luogu.org/problemnew/show/P2824
分析
一种思路就是直接二分,然后线段树操作一波,但是这是离线的
线段树合并与分裂就可以在线地做这道题
我们一开始把所有单个元素看成一颗权值线段树,然后1操作和2操作不断合并线段树即可
但是有一些要注意的地方,就是左右端点可能恰在某些线段树表示区间的中间,我们可以通过\(set\)查找出这种区间,这时候要分裂出来才能合并,同时降序和升序在分裂时需要分类讨论,其实降序的话直接把那段反过来算就好了,但还是比较烦人
同时还学到了一个像是垃圾回收节约内存的操作:
用一个栈或队列记录可以用的空节点,但感觉效果不是很显著
代码
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <iostream>
#include <queue>
#include <vector>
#include <set>
#define ll long long
#define ull unsigned long long
#define ri register int
#define pb push_back;
#define SIZE 1926081
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=getchar())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=getchar())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
using std::min;
using std::set;
using std::lower_bound;
const int maxn=200005;
const int N=2000005;
const int inf=0x7fffffff;
int n,m;
int sum[N<<2],ls[N<<2],rs[N<<2];
/*trash recycle*/
int st[N<<2],top=0;
inline void del(int x){st[++top]=x;}
inline int get_node(){int x=st[top];top--;sum[x]=ls[x]=rs[x]=0;return x;}
/*segment & set*/
struct Seg{
int l,r,rt,ty;//ty==0 increasing ty==1 decreasing
Seg(){l=r=rt=ty=0;}
Seg(int _l,int _r,int _rt,int _ty){l=_l,r=_r,rt=_rt,ty=_ty;}
bool operator <(const Seg &b)const{
return r==b.r?l<b.l:r<b.r;
}
};
set<Seg>se;
/*Segment Tree*/
int pos;
inline void pushup(int now){
sum[now]=sum[ls[now]]+sum[rs[now]];return ;
}
/*merge x and y to t*/
int merge(int x,int y){
if(!x)return y;
if(!y)return x;
int t=get_node();
sum[t]=sum[x]+sum[y];
ls[t]=merge(ls[x],ls[y]);
rs[t]=merge(rs[x],rs[y]);
del(x),del(y);
return t;
}
/*split now and put them to po*/
void split(int &now,int &po,int l,int r,int k){
if(!now)return ;
if(!po)po=get_node();
if(l==r){
sum[now]-=k,sum[po]+=k;
return ;
}
//printf("~~%d %d %d %d~~\n",now,po,l,r);
int tt=sum[ls[now]],mid=(l+r)>>1;
if(k<tt)split(ls[now],ls[po],l,mid,k);
else ls[po]=ls[now],ls[now]=0;
if(tt<k){
split(rs[now],rs[po],mid+1,r,k-tt);
}
pushup(now),pushup(po);
return ;
}
/*update*/
void update(int &now,int l,int r){
if(!now)now=get_node();
sum[now]++;
if(l==r)return ;
int mid=(l+r)>>1;
if(pos<=mid)update(ls[now],l,mid);
else update(rs[now],mid+1,r);
return ;
}
/*query pos_th in an increasing sequence*/
int query(int now,int l,int r){
if(l==r){
return l;
}
int mid=(l+r)>>1,tt=sum[ls[now]];
//printf("--%d %d %d %d %d--\n",now,l,r,tt,pos);
if(tt>=pos)return query(ls[now],l,mid);
pos-=tt;
return query(rs[now],mid+1,r);
}
Seg tmp=Seg(0,0,0,0);
set<Seg>::iterator it,pit;
inline int solve(int op,int l,int r){
int x;
tmp=Seg(0,l,0,0);
it=se.lower_bound(tmp);
tmp=*it;x=0;//printf("%d %d\n",tmp.l,tmp.r);
if(tmp.l!=l){
se.erase(it);
if(tmp.ty==0){
pos=l-tmp.l;
split(tmp.rt,x,1,n,pos);
se.insert(Seg(tmp.l,l-1,x,0));
se.insert(Seg(l,tmp.r,tmp.rt,0));
}
else{
pos=tmp.r-l+1;
split(tmp.rt,x,1,n,pos);
se.insert(Seg(tmp.l,l-1,tmp.rt,1));
se.insert(Seg(l,tmp.r,x,1));
}
}
//puts("sss");
tmp=Seg(0,r,0,0);
it=se.lower_bound(tmp);
tmp=*it,x=0;//printf("%d %d\n",tmp.l,tmp.r);
if(tmp.r!=r){
se.erase(it);
if(tmp.ty==0){
pos=r-tmp.l+1;
split(tmp.rt,x,1,n,pos);
se.insert(Seg(tmp.l,r,x,0));
se.insert(Seg(r+1,tmp.r,tmp.rt,0));
}
else{
pos=tmp.r-r;
split(tmp.rt,x,1,n,pos);
se.insert(Seg(tmp.l,r,tmp.rt,1));
se.insert(Seg(r+1,tmp.r,x,1));
}
}
x=0,it=se.lower_bound(Seg(0,l,0,0));
while(it!=se.end()&&(*it).r<=r){
tmp=*it;
x=merge(x,tmp.rt);
se.erase(it);
it=se.lower_bound(Seg(0,l,0,0));
}
se.insert(Seg(l,r,x,op));
//printf("**%d**\n",x);
return x;
}
int main(){
int x,y;
int op,l,r;
for(ri i=N;i>=0;i--)st[++top]=i;
read(n),read(m);
for(ri i=1;i<=n;i++){
read(x);//printf("%d\n",x);
y=get_node();
pos=x;
update(y,1,n);
se.insert(Seg(i,i,y,0));
}
//printf("()()(%d)()()\n",st[top]);
while(m--){
read(op),read(l),read(r);
solve(op,l,r);
//printf("()()(%d)()()\n",st[top]);
}
read(x);
y=solve(0,x,x);
pos=1;
printf("%d\n",query(y,1,n));
return 0;
}
luogu4197Peaks
https://www.luogu.org/problemnew/show/P4197
分析
在线做法Kruskal重构树
离线有种简单易懂的线段树合并解法,首先将边和询问的困难度都各自从小到大排序一遍,然后不断加边,直至边的困难度超过当前询问就换到下一个询问
然而不知道为何疯狂RE,太菜了
UPDATE: 感谢Ebola巨佬,指出了merge那里的错误就不会RE了,同时对拍时发现犯了个SB的错误,我直接输出了离散化后的编号...终于A了
注意这时候一颗线段树是表示一个联通块,合并时是要合并所在联通块所表示的根节点,使用并查集完成
代码
/*
Code By RyeCatcher
2018.10.9
*/
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cctype>
#include <vector>
#include <queue>
#include <utility>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#define ll long long
#define ull unsigned long long
#define pb push_back
#define ri register int
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define SIZE 1926081
using std::min;
using std::max;
using std::pair;
using std::queue;
using std::priority_queue;
using namespace __gnu_pbds;
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
#define gc getchar
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=getchar())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=getchar())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int maxn=500005;
const int N=2000005;
const int inf=0x7fffffff;
int st[N<<2],top=0;
int sum[N<<2],hi[100005],fa[100005];
int rt[100005],ls[N<<2],rs[N<<2];
int n,m,q;
struct Dt{
int x,id;
bool operator <(const Dt &b)const{
return x<b.x;
}
}dt[100005];
inline void init(){for(ri i=(N<<2)-10;i>=1;i--)st[++top]=i;}
inline void del(int x){st[++top]=x,sum[x]=ls[x]=rs[x]=0;return ;}
inline int get(){int x=st[top--];sum[x]=ls[x]=rs[x]=0;return x;}
gp_hash_table <int,int> g;int tot=0;
ll f[maxn];
struct Edge{
int x,y,dis;
Edge(){x=y=dis=inf;}
Edge(int _x,int _y,int _d){x=_x,y=_y,dis=_d;}
bool operator <(const Edge &b)const{
return dis<b.dis;
}
}edge[maxn];
int pos;
int get(int x){return (fa[x]==x)?fa[x]:(fa[x]=get(fa[x]));}
void update(int &now,int l,int r){
if(!now)now=get();
sum[now]++;
if(l==r)return ;
int mid=(l+r)>>1;
if(pos<=mid)update(ls[now],l,mid);
else update(rs[now],mid+1,r);
return ;
}
int query(int now,int l,int r,int k){
//printf("%d %d %d %d %d %d\n",now,l,r,k,sum[rs[now]]);
if(l==r){return l;}
int mid=(l+r)>>1,t=sum[rs[now]];
if(t>=k)return query(rs[now],mid+1,r,k);
if(sum[ls[now]]<k-t)return -1;
return query(ls[now],l,mid,k-t);
}
int merge(int x,int y){
if(!x||!y)return x+y;
sum[x]+=sum[y];
ls[x]=merge(ls[x],ls[y]);
rs[x]=merge(rs[x],rs[y]);
del(y);
return x;
}
int ans[maxn];
struct Query{
int v,k,x,id;
bool operator <(const Query &b)const{
return x<b.x;
}
}qry[maxn];
inline void solve(){
int tp=1,x;
int np=1,u,v;
while(tp<=q){
x=qry[tp].x;
//printf("**%d %d %d**\n",x,tp,qry[tp].id);
while(edge[np].dis<=x&&np<=m){
u=edge[np].x,v=edge[np].y;
//printf("--%d %d %d\n--\n",u,v,edge[np].dis);
u=get(u),v=get(v);
if(u!=v){
merge(rt[u],rt[v]);
fa[v]=u;
}
//puts("xx");
np++;
}
//printf("(%d)\n",n);
x=query(rt[get(qry[tp].v)],1,tot,qry[tp].k);
if(x==-1)ans[qry[tp].id]=-1;
else ans[qry[tp].id]=f[x];
tp++;
}
for(ri i=1;i<=q;i++)printf("%d\n",ans[i]);
return ;
}
int main(){
int x,y,z;
init();
memset(ans,-1,sizeof(ans));
read(n),read(m),read(q);
for(ri i=1;i<=n;i++){
read(dt[i].x);
dt[i].id=fa[i]=i;
}
std::sort(dt+1,dt+1+n);
for(ri i=1;i<=n;i++){
x=dt[i].x,y=dt[i].id;
if(!g[x]){
g[x]=++tot;
f[tot]=x;
}
hi[y]=g[x];
//pos=hi[y],update(rt[y],1,tot);
}
for(ri i=1;i<=n;i++){
pos=hi[i];
update(rt[i],1,tot);
}
for(ri i=1;i<=m;i++){
read(edge[i].x),read(edge[i].y),read(edge[i].dis);
}
std::sort(edge+1,edge+1+m);
for(ri i=1;i<=q;i++){
read(qry[i].v),read(qry[i].x),read(qry[i].k);
qry[i].id=i;
}
std::sort(qry+1,qry+1+q);
solve();
return 0;
}