听课笔记--DP--最大子矩阵和
最大子矩阵问题
给定一个n*n(0<n<=120)的矩阵,
矩阵内元素有正有负,
请找到此矩阵的内部元素和最大的子矩阵
样例输入:
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
样例输出:
15
-
方法一:
用二维前缀和维护然后一个个点遍历;
时间复杂度:O(N4);
-
方法二:
DP
先请明白这道题:
嗯?这不是一维的吗。和这道题有什么关系?
请看这张图:
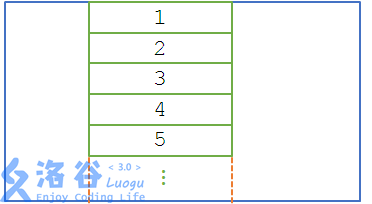
这样就不难看出,我们只要枚举区间的左端点l和右端点r; 同时用维护的二维前缀和求出每一段1,2,3,4,的值 然后竖着来一遍最大字段和(O(N))就好了 时间复杂度:O(N3)
代码:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=150;
int a[maxn][maxn];
int sum[maxn][maxn];
int line[maxn],c[maxn];
int l,r;
int n;
int solve()
{
int minx=min(0,line[1]),maxx=line[1];//
for(int i=2;i<=n;i++)
{
maxx=max(maxx,c[i]-minx);
minx=min(minx,c[i]);
}
return maxx;
}
int main()
{
int ans=-99999;
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
sum[i][j]=sum[i][j-1]+a[i][j];
}
}
for(r=1;r<=n;r++)
{
for(l=1;l<=r;l++)
{
for(int i=1;i<=n;i++)
{
line[i]=sum[i][r]-sum[i][l]+a[i][l];
c[i]=c[i-1]+line[i];
}
ans=max(solve(),ans);
memset(c,0,sizeof(c));
memset(line,0,sizeof(line));
}
}
cout<<ans<<endl;
return 0;
}


