基于最大似然准则的相关接收机

基于最大似然准则的相关接收机

学习《现代通信原理》（曹志刚）时，对其中相关接收机的近似阐述非常不解。借此机会，整理了大量课外资料，对相关接收机的原理有了比较清楚的认识。

• 基于最大似然准则的相关接收机
  • 1. 接收机的概念
    • 1.1 信号解调器
    • 1.2 检测器
  • 2. 相关解调器的解调过程及其原理
    • 2.1 构造相关解调器
    • 2.2 得到接收信号在基向量上的投影
    • 2.3 相关器输出的性质
  • 3. 检测器的实现及其数学原理
    • 3.1 MAP准则
    • 3.2 ML准则
    • 3.3 简化ML准则，实现检测器

1. 接收机的概念

接收机：由信号解调器和检测器组成。

1.1 信号解调器

功能：将接受波形\(r(t)\)变换为N维向量\(\boldsymbol r=[r_1,r_2,...,r_N]\)，N为发送信号波形的维数。

目的：求接受波形在各基向量上的投影，即求\(r_i\)。

实现方式：

1. 基于匹配滤波器的实现方法（匹配滤波器）。

2. 基于信号相关器的实现方法（相关解调器）。

1.2 检测器

根据信号解调器输出的N维向量\(r=[r_1,r_2,...,r_N]\)，判断发送波形。

发送信号波形的集合为\(\{S_m(t),m=1,2,...,M\}\)，维数为N。

2. 相关解调器的解调过程及其原理

2.1 构造相关解调器

根据发送信号波形集合\(\{S_m(t),m=1,2,...,M\}\)，构造正交基\(\{f_n(t),n=1,2,...,n\}\)

要求：每一个\(S_m(t)\)都可以表示为\(\{f_n(t)\}\)的线性加权组合：

\[S_m(t)=\sum_{k=1}^N {S_{mk}f_k(t)} \]

其中\(S_{mk}\)是在某个基向量上的幅度（投影）。

注意：尽管接收信号中会叠加信道噪声：

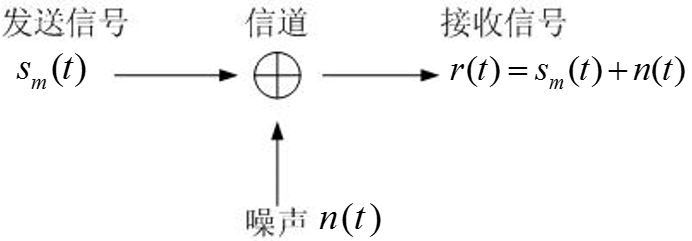
但在构造正交基\(\{f_n(t)\}\)时，我们不考虑噪声空间。因此接收信号会被分解为：

\[r(t)=\sum_{k=1}^N {S_{mk}f_k(t)}+n(t)=\sum_{k=1}^N {S_{mk}f_k(t)}+\sum_{k=1}^N {n_kf_k(t)}+n'(t) \]

其中\(n'(t)\)是无法用基函数组合的噪声组分。

至于为什么不考虑噪声空间，我们马上揭晓。

2.2 得到接收信号在基向量上的投影

令接收信号\(r(t)\)通过一组并行的N个互相关器：

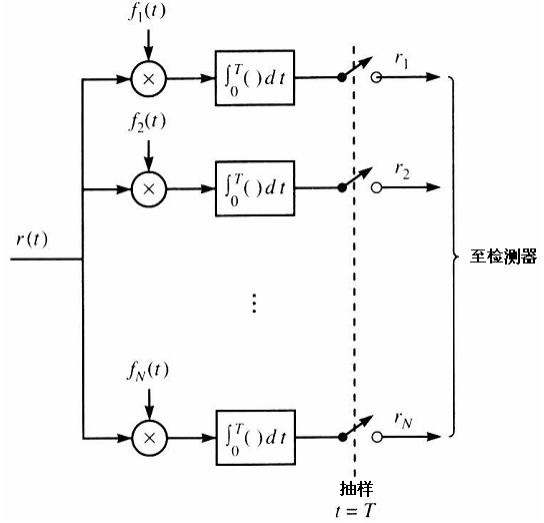
注意：在后面结合检测器，我们会对改图作改进和简化。因此这不是最终电路图！

各个相关器的输出为：

\[\int_0^T {r(t)f_k(t)dt} = S_{mk}+n_k　＝　r_k \]

\(S_{mk}\)就是我们想要的投影，\(n_k\)是噪声的投影，是一个高斯随机变量，由信道引入的加性噪声决定。

而无法被基向量表示的\(n'(t)\)（在线性空间外），积分为０（由于噪声均值为０，因此不相关和正交等价），因此对输出没有任何影响！
这就是为什么我们在构造正交基时，不考虑噪声空间！

2.3 相关器输出的性质

由于\(S_{mk}\)是一个确定的值，而\(n_k\)是一个高斯随机变量，因此：
\(r_k\)也是一个高斯随机变量，其均值为\(S_{mk}\)，方差同\(n_k\)，为\(\frac{n_0}{2}\)。

因此，相关解调器最终输出的Ｎ维向量\(\boldsymbol r=[r_1,r_2,...,r_N]\)，其概率满足联合高斯分布：

\[P(\boldsymbol r|\boldsymbol S_m) = \prod_{k=1}^N {P(r_k|S_{mk})} \\=\frac{1}{(\sqrt{2\pi\frac{n_0}{2}})^N}exp[\frac{-\sum_{k=1}^N{(r_k-S_{mk})^2}}{2\frac{n_0}{2}}] \]

3. 检测器的实现及其数学原理

尽管相关器已经为我们得到了一个满足联合高斯分布的Ｎ维向量，但由于噪声的存在，为了使判错率最小，我们还需要合理地选出最合适的波形，作为最终判断结果。

3.1 MAP准则

全称为最大后验概率Maximum A posteriori Probability，其中A posteriori在拉丁文中是“后验”的意思。

根据推导（参见信息论相关书籍），选择后验概率\(P(\boldsymbol S_m|\boldsymbol r)\)最大对应的发送信号\(S_m(t)\)作为判断结果，则错误率最小。
这一点也很好理解。在接收到\(r(t)\)并转换得到\(\boldsymbol r\)的条件下，发送信号最有可能是\(S_m(t)\)，那么我们当然选择它作为输出结果啦～

可惜的是，后验概率很难通过电路获得。
因此，我们无法直接利用MAP准则。

3.2 ML准则

全称为最大似然Maximum Likelihood。

根据贝叶斯公式：

\[P(\boldsymbol S_m|\boldsymbol r)=\frac{P(\boldsymbol S_m,\boldsymbol r)}{P(\boldsymbol r)}=\frac{P(\boldsymbol r|\boldsymbol S_m)P(\boldsymbol S_m)}{\sum_{i=1}^M{P(\boldsymbol r|S_i)P(S_i)}} \]

其中：

• \(P(\boldsymbol S_m)\)是先验概率，一般设为等概。

• \(P(\boldsymbol r)=P(\boldsymbol r|S_i)P(S_i)\)与发送信号无关。因为无论发的是哪个\(P(\boldsymbol S_m)\)，\(P(\boldsymbol r)\)都是既定的，客观存在且无法改变的。具体而言，其中的先验概率\(P(S_i)\)和发送概率\(P(\boldsymbol r|S_i)\)都不随发送信号的变化而改变。

这么看来，我们有重要结论：

• 当\(P(\boldsymbol S_m)\)等概时，最大的\(P(\boldsymbol S_m|\boldsymbol r)\)，对应最大的\(P(\boldsymbol r|\boldsymbol S_m)\)！这就是MAP准则到ML准则的转化！

• 当不等概时，最大的\(P(\boldsymbol S_m|\boldsymbol r)\)，对应最大的\(P(\boldsymbol r|\boldsymbol S_m)P(\boldsymbol S_m)\)，稍微复杂一些，但也很好求。

先剧透一波，ML准则非常容易通过电路实现！我们接着看～

3.3 简化ML准则，实现检测器

现在我们讨论\(P(\boldsymbol S_m)\)等概的情况，即ML准则可以使用。

由第一部分我们知道：解调器输出为：

\[P(\boldsymbol r|\boldsymbol S_m)=\frac{1}{(\sqrt{2\pi\frac{n_0}{2}})^N}exp[\frac{-\sum_{k=1}^N{(r_k-S_{mk})^2}}{2\frac{n_0}{2}}] \]

我们取对数：

\[ln[P(\boldsymbol r|\boldsymbol S_m)]=-\frac{N}{2}ln(\pi n_0)-\frac{\sum_{k=1}^N{(r_k-S_{mk})^2}}{n_0} \]

显然，第一项是常数，对判断发送信号没有贡献。

第二项是关于\(\sum_{k=1}^N{(r_k-S_{mk})^2}\)单调的函数。
因此，最大后验概率，对应着最小的欧氏距离：

\[D(\boldsymbol r,\boldsymbol S_m)=\sum_{k=1}^N{(r_k-S_{mk})^2} \]

因此，基于ML准则的判决，又称为最小距离检测。

进一步展开、化简得到：

\[D(\boldsymbol r,\boldsymbol S_m)=\sum_{k=1}^N{(r_k)^2}+\sum_{k=1}^N{(S_{mk})^2}-2\sum_{k=1}^N{r_kS_{mk}} \]

其中：

• 第一项是向量\(\boldsymbol r\)的模值，对判断没有贡献。

• 第二项是接收信号的能量：\(\varepsilon_m\)，与发送信号有关，需要考虑。

• 第三项是投影，显然也需要考虑：

  \[2\sum_{k=1}^N{r_kS_{mk}}=2\boldsymbol r\bigodot \boldsymbol S_m = 2 \int_0^T {r(t)S_m(t)}dt \]

我们把需要考虑的后两项的相反数合称为相关度量：

\[C(\boldsymbol r, \boldsymbol S_m)=2\sum_{k=1}^N{r_kS_{mk}}-\varepsilon_m \]

综上，我们得到判断的最终准则：
最大相关度量\(C(\boldsymbol r, \boldsymbol S_m)\)对应的发送信号\(S_m(t)\)，就是最终判决结果。

因此，我们希望整个相关接收机实现如下流程：

• 将接收信号\(r(t)\)转换为N维向量\(\boldsymbol r\)

• 求出\(\boldsymbol r\)和各个\(\boldsymbol S_m\)的相关度量\(C(\boldsymbol r, \boldsymbol S_m)\)

• 选择最大相关度量对应的发送信号波形\(S_m(t)\)输出

最终电路图（相关接收机）如下：

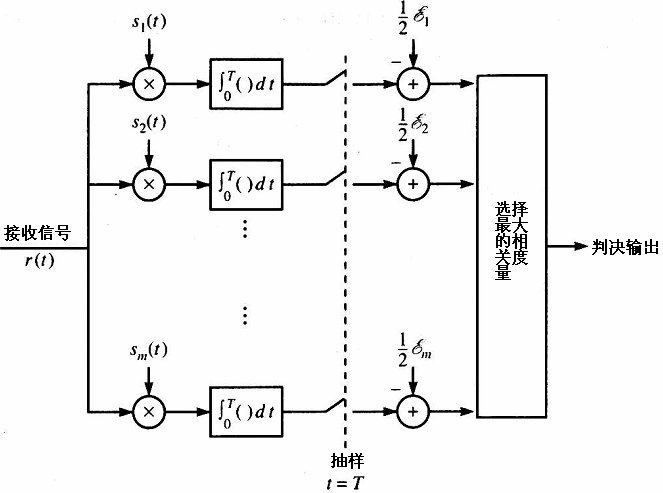
如果发送波形不等概率，那么MAP准则就不可以直接转换为ML准则啦。此时只需要寻找最大\(P(\boldsymbol r|\boldsymbol S_m)P(\boldsymbol S_m)\)对应的发送波形，化简方式类似，这里就不赘述了。