Paper | Learning convolutional networks for content-weighted image compression
Learning convolutional networks for content-weighted image compression
发表在2018年CVPR。
以下对于一些专业术语的翻译可能有些问题。
摘要
-
有损压缩是一个优化问题，其优化目标是率失真，优化对象是编码器、量化器和解码器（同时优化）。
Lossy image compression can be formulated as a joint rate-distortion optimization to learn encoder, quantizer, and decoder.
-
其中，量化器和离散熵预测（discrete entropy estimation）是不可差分的，因此要将压缩系统用CNN替换是很困难的。
-
作者认为，我们可以根据图像的局部内容，来决定图像中每一个区域的重要性，从而控制每一个区域的码率分配，从而替换掉离散熵估计。
-
此外，作者还采用了一个二元机（binarizer）来实现量化功能。为了让二元机在BP过程中可差分，作者引入了一个代理函数（proxy function），在BP中代替二元操作。
-
此时，编码器、解码器、二元机和权重图是可以端到端优化的。
-
为了实现无损压缩，作者还引入了卷积熵编码器。
-
实验发现，在低码率图像压缩条件下，算法的SSIM指标超过了JPEG和JPEG 2000。
故事要点
-
一个图像压缩系统通常需要包括以下三个组分：编码器（encoder），量化器（quantizer）和解码器（decoder）。这才能组成一个编解码器（codec）。
-
JPEG和JPEG 2000为什么不够好呢【有哪些提升空间呢】？首先，它们都依赖于主观设计的图像变换方法，并且需要对各组分独立优化。从效果上，在低码率压缩时二者表现都很差，会产生模糊、振铃和块效应等。
-
CNN为什么有取而代之的潜力呢？因为：复杂的非线性分析和生成变换过程，都可以用几层CNN实现。此外，CNN结构还可以让编码器和解码器联合优化。
-
尽管基于深度学习的工作很多，但仍有许多问题亟待解决。首先，我们如何解决量化器的不可差分特性？其次，由于我们的学习目标是 同时最小化 压缩率和失真，因此我们要衡量熵率（entropy rate）。如何 连续地近似 用离散码元定义的 离散熵率？
-
因此，本文的目标就是解决（1）量化和（2）熵率预测问题。
-
现有的深度学习方法，为每一个位置都分配相同长度的码元。显然，局部信息量（local informative content）是空域变化的，因此比特率也应该是空域变化的。因此作者提出了一个基于内容权重的重要性图（content-weighted importance map）。其输出一个与输入同尺寸的图。每一个点的值是一个非负数值，指示编码长度。此时，重要性图各点求和，就可以作为压缩率的连续预测，进而作为压缩率控制器。此时，我们就不再需要预测熵率了。
-
二元机很简单：首先对特征图取sigmoid函数，输出大于0.5的则归为1，否则为0。在反向传播时，该二元机被一个代理函数近似。
-
此时，整体网络就可以联合优化。如图：
-
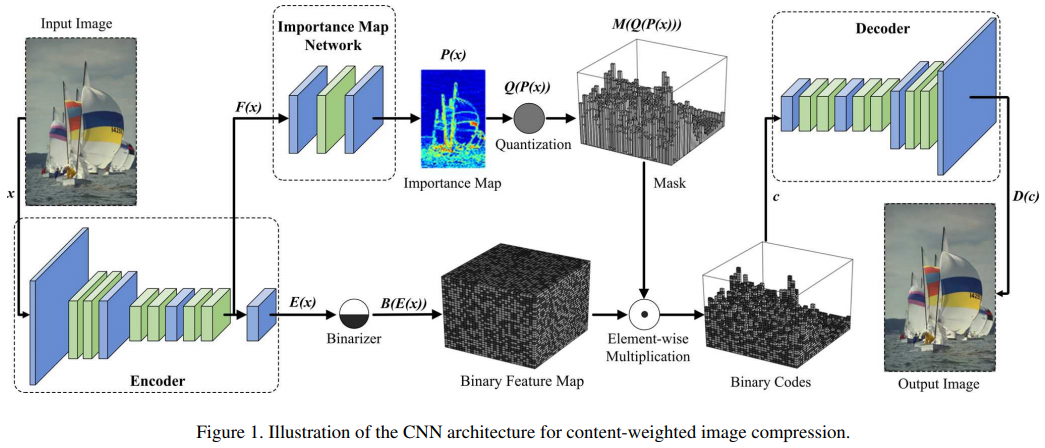
注意：在传统方法中，编码是基于上下文（context）的。为此，作者采用了[14]提出的基于上下文的自适应二进制算术编码方法CABAC，进一步压缩二进制码元和重要性图。
本来我是想看一看重要性图怎么生成的。看到上图就知道了，就是简单的CNN网络。因此方法没再细看。
以我的经验，这种方案最难的是训练。我们直接看看作者怎么训练的。
模型训练
前面提到了，我们要同时最小化压缩率和失真。因此损失函数设为两个加权组合：
其中，MSE是从解码器解码出来的图像，与原图像的\(L_2\)范数。R是码率损失。作者设置了一个阈值\(r\)，若重要性图的求和大于\(r\)，则损失为和；否则为0。总的损失是batch中每一张图像损失的总和。
在实际训练时，作者先抛开重要性图，让编码器解码器主体先收敛；然后按三个阶段训练，学习率分别是\(1e^{-4}\)、\(1e^{-5}\)和\(1e^{-6}\)。每个阶段都训练到损失函数不再下降为止。
\(\gamma\)和\(r\)根据需要可调。
