Paper | SkipNet: Learning Dynamic Routing in Convolutional Networks

SkipNet: Learning Dynamic Routing in Convolutional Networks

• SkipNet: Learning Dynamic Routing in Convolutional Networks
  • 1. 概括
  • 2. 相关工作
  • 3. 方法细节
    • 门限模块的结构
    • 训练方法
  • 4. 总结

作者对residual network进行了改进：加入了gating network，基于上一层的激活值，得到一个二进制的决策0或1，从而继续推断或跳过下一个block。作者还提出了对应的训练方法，集成有监督学习和强化学习，从而克服了skipping不可差分的问题。

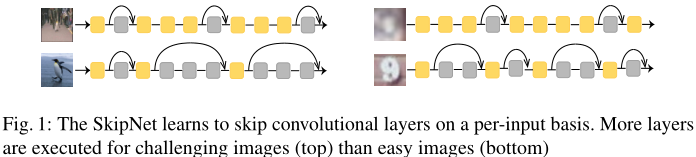
1. 概括

难点：skipping决策是不可差分的，那么就无法用基于梯度的优化方法进行学习。

1. [2,30,31]提出了软近似，但实验发现它们的精度很差。

   We show that the subsequent hard thresholding required to reduce computation results in low accuracy.

2. [4,23]则提出用强化学习解决硬判决问题，但实验发现它们很脆弱，即精度也很差。

3. [16,21]还采用了reparametrization技术，但其中的松弛会引入估计误差，导致习得策略欠佳。

训练方法大致分为2步：

1. 借助reparameterization和soft-max松弛，同时训练网络和门限。

2. 取消松弛，借助强化学习，继续精炼skipping政策。

实验结果：在CIFAR-10、CIFAR-100、SVHN和ImageNet上，分别能降低50%、37%、86%和30%的计算量。并且，SkipNet也存在一个超参数，可以针对不同计算量约束进行调节。

2. 相关工作

为了实现模型压缩，大多数工作集中在参数稀疏化、滤波器剪枝，向量量化和蒸馏。这些方法的共同问题：

1. 通常是后处理，即对已经训练好的网络执行的操作。

2. 并不能根据输入动态调整网络。

还有一些工作[6,8,29]通过提前终止实现这一目标。其中[8]是暂停循环过程，[6]和[29]是提前终止CNN。但本文的SkipNet是跳过而不是提前终止。

还有一些工作[1,22,32]集成了不同计算复杂度的多个模型，并设计决策机制或终止机制。但是这样做严重浪费了存储，并且每个模型并不存在计算共享。

3. 方法细节

基本方法就是：在ResNet的基础上，加入了门限网络。其将上一层的输入映射至0或1，从而跳过或执行下一层。

注意：要求输入、输出的维度相同。而ResNet的块结构正好满足这一要求。或者要采用池化等操作。

门限模块的结构

作者尝试了三种结构：

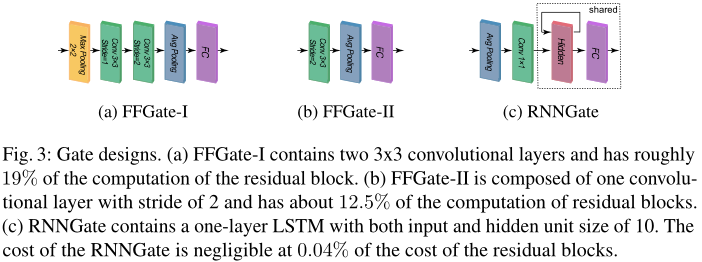
前两种都是CNN结构，第三种是RNN结构。第一种计算量大，作者只用于浅层网络；第二种计算量小，作者用于超过百层的网络。在后续实验中，作者发现循环网络效果最好，不仅计算量远小，而且精度也高。这归功于其时序学习能力。

训练方法

最简单直接的方法就是用softmax软化（例如Highway Networks），使得网络参数能够差分；而在推导（测试）时再用硬判决。但实验发现其精度很差，原因是其中存在误差。

作者决定在训练阶段保留硬判决。现在我们分析损失函数。假设第\(i\)层的输入是\(\mathbf{X}^i\)，门模块是\(G^i(\mathbf{X}^i)\)，判决结果是\(g_i\)。\(g_i = 1\)时，该层执行；\(g_i = 0\)时，该层被跳过（输入直接恒等映射至输出）。一共\(N\)层，则总判决为\(\mathbf{g} = \{0, 1\}^N\)。

假设网络每一层参数的集合（包括门模块）为：\(F_{\theta} = [F_{\theta}^1, ..., F_{\theta}^N]\)。在给定\(\mathbf{X}\)和\(\mathbf{g}\)的情况下，损失为：

\[L_{\theta}(\mathbf{g}, \mathbf{X}) = \mathcal{L}(\hat{y}(\mathbf{X}, F_{\theta}, g), y) - \frac{\alpha}{N} \sum_{i=1}^N (1 - g_i) C_i \]

前半部分应该是有监督学习中的保真度（fidelity）或者准确度指标之类的【作者没提】，后者惩罚的是计算量。其中\(C_i\)用来调节\(F_i\)的重要性【注意负号】，作者设恒为1。\(\alpha\)是权衡计算量和精度的超参数。

进一步，右半部分可以视为强化学习中的奖励（reward）。

我们的训练目标严格写是这样：

\[\min \mathcal{J}(\theta) = \min \mathbb{E}_{\mathbf{X}} \mathbb{E}_{\mathbf{g}} L_{\theta}(\mathbf{g}, \mathbf{X}) \]

即：对训练集中的所有样本取统计平均（一般就是平权，因为假设i.i.d.），对所有可能的判决集结果取统计平均，并最终实现 最小化误差的同时 最小化计算量。二者相对重要性由\(\alpha\)调控。

我们也可以看看该训练目标函数的梯度。注意梯度是关于参数\(\theta\)的梯度：

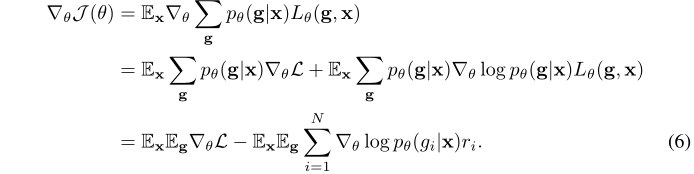
第二步的右半部分是这样的，熟悉RL的同学都很清楚：

\[\nabla_{\theta} \log p_{\theta}(\mathbf{g} | \mathbf{X}) = \frac{1}{p_{\theta}(\mathbf{g} | \mathbf{X})} \nabla_{\theta} p_{\theta}(\mathbf{g} | \mathbf{X}) \]

对于最终结果，左半部分就可以看作监督学习损失函数的梯度，右半部分就可以看作强化学习损失的梯度。其中：

\[r_i = - [\mathcal{L} - \frac{\alpha}{N} \sum_{j=i}^N R_j] \]

在实际操作中，我们降低对精度的要求，给前半部分加一个超参数：

\[r_i = - [\beta \mathcal{L} - \frac{\alpha}{N} \sum_{j=i}^N R_j] \]

作者设\(\beta = \frac{\alpha}{N}\)或1。

实际上，分两个部分分别训练是不完美的，但是一个折衷的处理方式。作者首先使用监督学习，让网络参数初步收敛。然后再采用强化学习。实验发现，如果直接将上式作为强化学习的激励，那么训练效果会很不好。原因可能是学习的策略过早收敛于垃圾特征。

实验有几个有趣的发现：

1. 简单的样本（跳过层数多）偏亮，清晰，对比度高：

   

2. 越大尺度的图像平均需要块越多（可能因为感受野不够）：

   

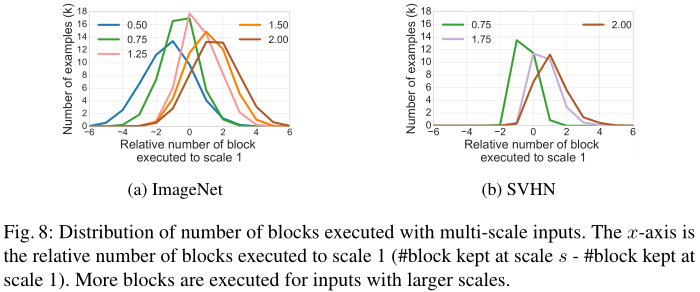
3. 前面层和后面层被跳过比较频繁，中间层跳过率很低。

4. 有监督预训练为强化学习提供了很好的起点。

5. 在计算量相同的情况下，硬判决的精度远高于软判决。

4. 总结

优点：不同于提前退出，这种方法比较新。

不足：每一层或块的输入、输出维度必须相同，否则无法执行跳过判决（跳过或执行的输出维度必须得一致）。或者需要池化等额外操作。