主成分分析法(离散K-L变换)
主成分分析法(离散K-L变换)
1. 概述
全称:Discrete Karhunen–Loève Transform (KLT)
离散K-L变换来源于祖宗PCA(Principal component analysis)。参见维基百科
-
PCA方法在1901年由Karl Pearson提出。在上世纪30年代,Harold Hotelling开拓了PCA的应用方向。
-
PCA在信号处理领域称为Discrete Karhunen–Loève Transform (KLT),也就是我们今天的主角;在多变量质量控制领域称为the Hotelling transform,等等。
目的:将原始特征转换为数量较少的新特征。
特点:
-
适用于任意概率密度函数
-
最小均方误差意义下的最优正交变换
-
在消除模式特征之间的相关性、突出差异性方面具有最优效果
2. K-L变换方法和原理推导
2.1 向量分解
对列向量\(\boldsymbol x\),我们用确定的完备正交归一向量系\(\{\boldsymbol u_j\}\)展开:
其中在某个基向量\(\boldsymbol u_j\)上的投影为:
这是惯用方法了。
2.2 向量估计及其误差
出于压缩数据等目的,我们往往用有限项估计\(\boldsymbol x\),即:
估计引入的均方误差为:
注意,上式之所以这么写,是为了满足矩阵乘法,最终得到一个实数\(y_j^2\)。
对于一组确定的基向量,\(\boldsymbol u_j\)是常量而不是变量,因此上式可以简化为:
其中,\(R=E[\boldsymbol x \boldsymbol x^T]\)是自相关矩阵(因为\(\boldsymbol x\)是列向量),当输入向量\(\boldsymbol x\)给定时,该矩阵就是确定的。
因此,要使估计误差\(\epsilon\)最小,就要求合理选择归一正交向量系\(\{\boldsymbol u_j\}\)。
2.3 寻找最小误差对应的正交向量系
由拉格朗日乘子法,构造:
对每一个\(\boldsymbol u_j\)求偏导,并令其为0,得:
其中用到二次型求偏导的结论,参见博文:二次型求偏导
简化得:
这意味着:当我们选取\(\boldsymbol R\)的特征向量作为正交向量系\(\{\boldsymbol u_j\}\)时,可以取得误差极值!\(\lambda_j\)即对应特征值。
这里虽然下标从\(d+1\)开始,但正是因为估计采用的是特征向量系,因此误差也继续沿用特征向量系。
进一步,估计误差的极值为:
这意味着:如果我们选取最大特征值对应的特征向量系,作为正交向量系,那么估计误差将会是最小的!
同理,我们是把大特征值的用作估计,因此剩下小特征值的给误差。
因此我们得到了K-L变换本质方法:取\(\boldsymbol R\)的\(d\)个最大特征值对应的特征向量,作为正交基向量展开\(\boldsymbol x\)。此时截断均方误差最小。

这\(d\)个特征向量组成的正交坐标系,称为\(\boldsymbol x\)所在的\(D\)维空间的\(d\)维K-L变换坐标系,而展开系数向量\(\boldsymbol y\)称为\(\boldsymbol x\)的K-L变换。
最后注意一个技术细节:数据去均值。
前面我们学习的,实际上只针对单个数据:(列)向量\(\boldsymbol x\)。
但实际应用中,我们往往会对多个列向量组成的矩阵\(\boldsymbol X\)执行PCA任务。
推广过程类似,在第四节介绍。根据结论,我们往往会直接取矩阵\(\boldsymbol {XX^T}\)的自协方差矩阵,来获得特征值。
由于自协方差是二阶中心距,因此我们要对数据进行中心化。即把\(\boldsymbol x\)看作是随机变量\(\mathrm x\)的取值,要求\(\mathbb E(\mathrm x) = \boldsymbol 0\)。
比如,我们有两个点:(4,1)和(-2,-3)。那么我们求每个维度上的均值:1和-1,处理后的数据点为:(3,2)和(-3,-2)。
3. K-L变换高效率的本质
我们不妨看一看变换后的\(\boldsymbol y\)的自相关矩阵:
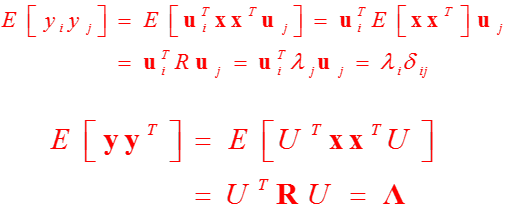
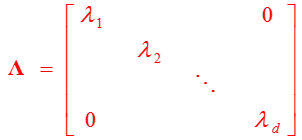
变换后的结果是对角阵!即元素是彼此不相关的。这是K-L变换用于高效数据压缩的杀手锏。
实际上,PCA是寻找输入空间中的一个旋转,使得方差的主坐标,和新表示空间的基坐标对齐。如P92简单例的示意图。
可惜的是,该变换不具有分离性,二维不可分,缺少快速算法。
4. PCA在编、解码应用上的进一步推导
梳理自《DEEP LEARNING》。
4.1 编、解码函数的定义
待编码的点为\(\boldsymbol x \in \mathbb R^n\)
编码函数为\(\boldsymbol c= f(\boldsymbol x) \in \mathbb R^l\),\(l<n\),以节约存储空间。
解码函数为\(g(\boldsymbol c)\),希望的效果为\(g(\boldsymbol c) \approx \boldsymbol x\)
为了简化,我们用矩阵乘法的形式实现解码器。即\(g(\boldsymbol c)=\boldsymbol {Dc},\boldsymbol D \in \mathbb R^{n*l}\)
其实大家也看出来了,这里解码的思想,仍然是用数目较少的向量,来估计高维的向量\(\boldsymbol x\)。所以才写成矩阵乘法的形式。
4.2 寻找最优编码\(\boldsymbol c^*\)
4.2.1 构造、简化优化函数
我们可以采用\(L^2\)范数,来衡量原始输入\(\boldsymbol x\)和重构向量\(g(\boldsymbol c)\)的距离。
这里需要强调一点:我们是在寻找最优编码\(\boldsymbol c^*\)!即当解码函数\(\boldsymbol D\)给定时,如何编码得到\(\boldsymbol c^*\),使得衡量原始输入\(\boldsymbol x\)和重构向量\(g(\boldsymbol c^*)\)之间的距离最小。
即解码流程已定,只需要考虑编码,但最终效果是解码后误差最小。
为了进一步推导,我们利用平方\(L^2\)范数。
由于\(L^2\)范数是非负的,并且平方运算在非负值上是单调的,因此二者会在相同的最优编码\(\boldsymbol c^*\)上取得最小值:
由分配律(矩阵乘法服从分配律和结合律,不服从交换律),展开得:
其中\(g(\boldsymbol c)^T \boldsymbol x\)是标量,所以转置等于自己。
在上式中,第一项不依赖于\(\boldsymbol c\),因此我们的优化目标简化为后两项:
代入\(g(\boldsymbol c)\)定义:
为了简化问题,我们规定\(\boldsymbol D\)中的列向量是相互正交的。要注意不是正交矩阵,因为一般不是方阵。
此外,为了保证\(\boldsymbol D\)有唯一解,我们规定\(\boldsymbol D\)中所有列向量都只有单位范数。
基于这两点假设,我们就可以得到非常简洁的表达式:
4.2.2 最优编码函数
我们对上式求\(\boldsymbol c\)的偏导,令其为0,得:
这意味着:最优编码同样利用矩阵乘法,非常高效。
复原的向量为:
4.3 寻找最优编码矩阵\(\boldsymbol D^*\)
实际上,待处理的\(n\)维点有多个:\(\{\boldsymbol x^{(i)},i=1,2,...\}\),因此\(\boldsymbol D\)必须是整体最优设计。
上一节只针对单个点\(\boldsymbol x\)进行讨论,是因为最终结果只与\(\boldsymbol D\)有关。因此我们现在再全面讨论\(\boldsymbol D\)即可。
因此优化函数为:
这是矩阵之间的Frobenius范数。
之后的推导运用了迹运算的性质等,结论相同:最优矩阵\(\boldsymbol D\)由\(\boldsymbol {XX^T}\)前\(l\)个最大特征值对应的特征向量组成。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号