Paper | Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
- Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
1. 尺度空间理论(scale-space theory)
参考:维基百科
如果我们要处理的图像目标的大小/尺度(scale)是未知的,那么我们可以采用尺度空间理论。
其核心思想是将图像用多种尺度表示,这些表示统称为尺度空间表示(scale-space representation)。我们对图像用一系列高斯滤波器加以平滑,而这些高斯滤波器的尺寸是不同的。这样,我们就得到了该图像在不同尺度下的表示。
公式化:假设二维图像为\(f(x,y)\),二维高斯函数(关于\(t\)的簇)为\(g(x,y;t) = \frac{1}{2{\pi}t}e^{-\frac{x^2+y^2}{2t}}\),那么线性尺度空间就可以通过二者卷积(Convolution)得到:
高斯滤波器的方差\(t = \sigma^2\)被称为尺度参数(scale parameter)。
直观地看,图像中尺度小于\(\sqrt{t}\)的结构会被平滑地无法分辨。因此,\(t\)越大,平滑越剧烈。
实际上,我们只会考虑\(t \ge 0\)的一些离散取值。当\(t = 0\)时,高斯滤波器退化为脉冲函数(impulse function),因此卷积的结果是图像本身,不作任何平滑。
看图:

事实上,我们还可以构造其他尺度空间。
但由于线性(高斯)尺度空间满足很多很好的性质,因此是使用最为广泛的。
尺度空间方法最重要的属性是尺度不变性(scale invariant),使得我们可以处理未知大小的图像目标。
最后要注意的是,在构造尺度空间时,往往还伴随着降采样。
比如\(t=2\)的尺度空间,我们会将其分辨率减半,即面积减为\(1/4\)。这也是本文的做法。
2. OctConv
作者认为:不仅自然世界中的图像存在高低频,卷积层的输出特征图以及输入通道(feature maps or channels)也都存在高、低频分量。
低频分量支撑的是整体,比如企鹅的白色大肚皮。显然,低频分量是存在冗余的,在编码过程中可以节省。
基于以上考虑,作者提出OctConv用以取代传统CNN(vanilla CNN)。有以下两个关键步骤:
第一步,我们要获得输入通道(或图像)的线性尺度表示,称为Octave feature representation。
所谓高频分量,是指不经过高斯滤波的原始通道(或图像);所谓低频分量,是指经过\(t=2\)的高斯滤波得到的通道(或图像)。
由于低频分量是冗余的,因此作者将低频分量的通道长/ 宽设置为高频分量通道长/ 宽的一半。
在音乐中,Octave是八音阶的意思,隔一个八音阶,频率会减半;在这里,drop an octave就是通道尺寸减半的含义。
那么高频通道和低频通道比例是多少呢?作者设置了一个超参数\(\alpha \in [0,1]\),表示低频通道的比例。在本文中,输入通道低频比例\(\alpha_{in}\)和输出通道低频比例\(\alpha_{out}\)设为相同。
图:企鹅白肚皮(低频)冗余(上);传统CNN,OctConv对比(下)。
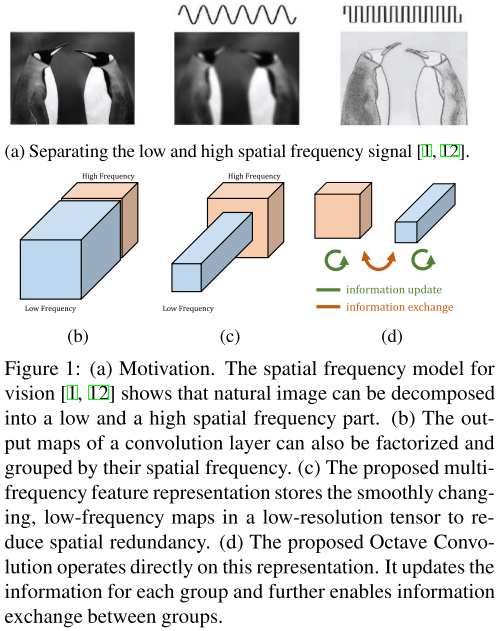
问题来了:由于高/ 低频通道尺寸不一,因此传统卷积无法执行。
但我们又不能简单地对低频通道进行升采样,因为这样不就白干了嘛,计算量和内存就没办法节省了。
因此我们有第二步:
第二步,作者提出了对应的卷积解决方案:Octave Convolution。
首先给一些定义:
设图像的低频分量和高频分量分别是\(X^L\)和\(X^H\),卷积输出的低频分量和高频分量分别是\(Y^L\)和\(Y^H\)。卷积操作中,\(W^H\)负责构建\(Y^H\),\(W^L\)负责构建\(Y^L\)。
我们希望:
\(W^H\)既有负责\(X^H\)到\(Y^H\)的部分:\(W^{H \to H}\),也有负责\(X^L\)到\(Y^H\)的部分:\(W^{L \to H}\),即\(W^H = [W^{H \to H}, W^{L \to H}]\)。
其结构如下图右边所示。
其中,\(W^{H \to H}\)是传统卷积,因为输入、输出图像尺寸一样大;对于\(W^{L \to H}\)部分,我们先对输入图像进行升采样(upsample),再执行传统卷积。这样,整体计算量仍然是减少的。
\(W^L\)同理,但对\(W^{H \to L}\)先执行的是降采样。
具体方法很简单,就是取值的问题:

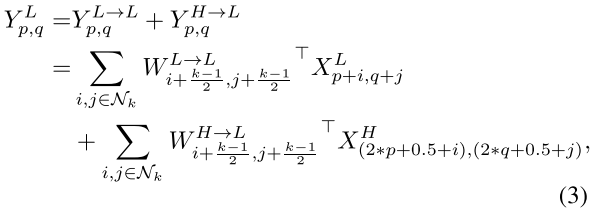
降采样后卷积相当于有步长的卷积,会不太精确;因此作者最后选择了平均池化(pooling)的方式,平均取值,采样结果会较精确一些。
完整流程如图左:
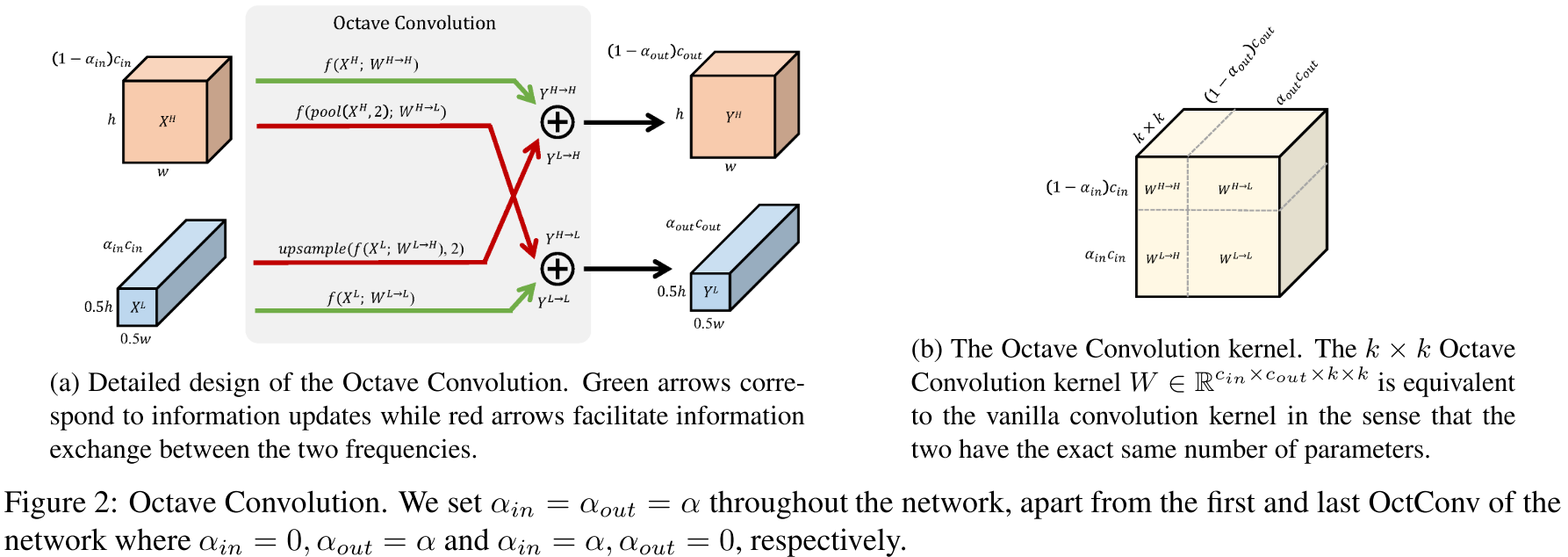
整套流程下来,我们可以发现,这种滤波+新式卷积的操作是“插片式”的,不需要破坏原来的CNN框架。
值得注意的是,低频通道卷积的感受野比传统卷积更大。
通过调整低频比例\(\alpha\),预测精度和计算代价可以得到权衡(trade-off)。
实验效果:在算力受限的情况下(内存消耗低),图像分类的预测精度相当高。见论文。
3. 启发
-
我们要让神经网络更好地学习。
该文通过尺度空间变换和Octave卷积操作,让网络更清晰地分开处理高、低频分量,并且在低频分量上节约了计算量。
又比如BN技巧,也是让网络自我学习\(\alpha\)和\(\beta\)参数,从而实现特征中心化。
神经网络很厉害,自学能力超强,但我们要适度改造它,让它更快、更精简、更强大。
-
我们要多从人类视觉特性上思考问题。
因为人类视觉编码的能力远远超过现有技术:分辨率大概是10亿像素(10亿个视杆/视锥细胞),但眼睛到大脑的通路带宽只有8Mbps(1k个神经节)。
本文思考的低频分量冗余,很有可能就是人类视觉编码特性中主要解决的冗余之一。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号